資料結構與演演算法 | 圖(Graph)
在這之前已經寫了陣列、連結串列、二元樹、棧、佇列等資料結構,本篇一起探究一個新的資料結構:圖(Graphs )。在二元樹裡面有著節點(node)的概念,每個節點裡麵包含左、右兩個子節點指標;比對於圖來說同樣有著節點(node),在圖裡也稱為頂點(vertex),頂點之間的關聯不在侷限於2個(左、右),一個頂點可以與任意(0-n個)個頂點進行連結,這稱之為邊(edge)。 一般會把一個圖裡面頂點的集合記作 V ,圖裡面邊的集合記作 E,圖也就用 G(V,E) 來表示。
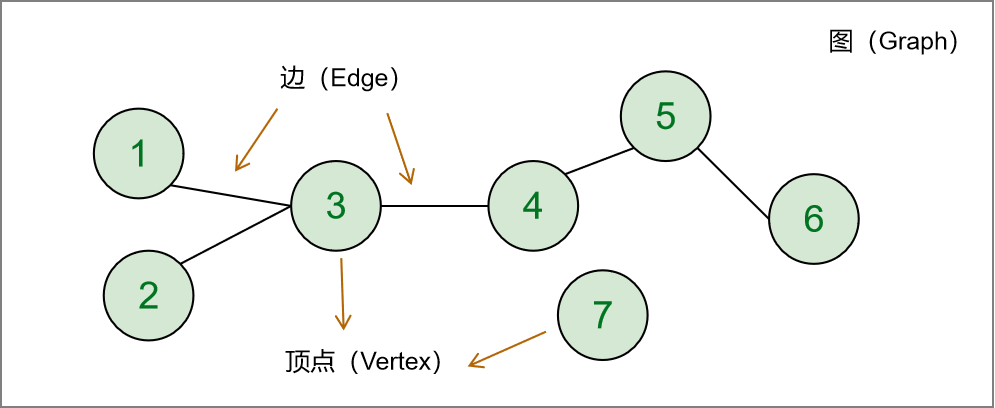
對比二元樹可以看到圖的約束更少,換一個角度看二元樹結構是圖的特殊形式,所謂特殊形式指加上更多的限定條件。
圖的分類(Types Of Graph)
可以看到圖的基本的結構非常簡單,約束也很少,如果在其中加上各種條件約束就可以定義各種型別的圖。
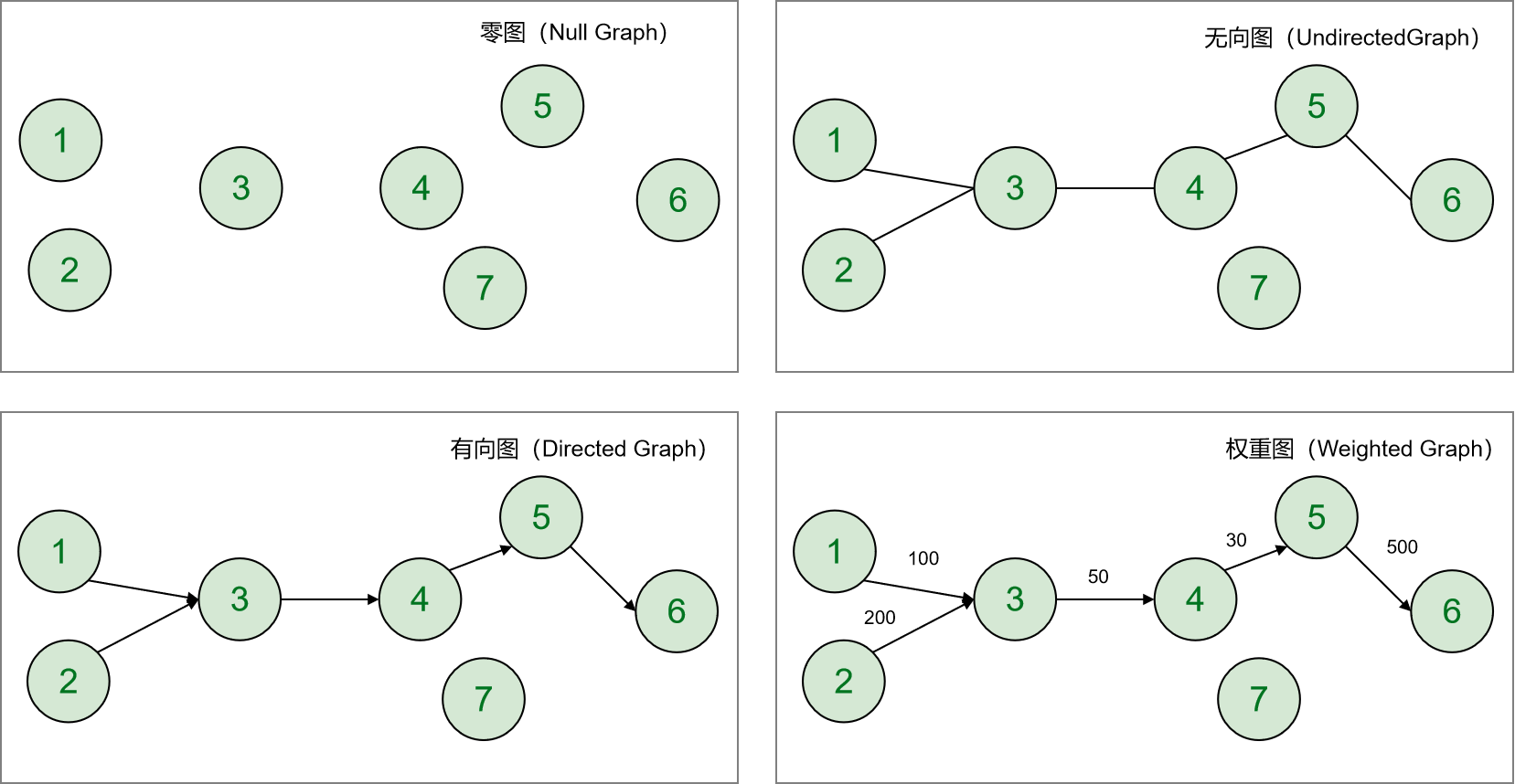
- 約束邊或者頂點個數來分類:
零圖(Null graph):只有頂點沒有邊的圖;平凡圖(Trivial graph):只有一個頂點的圖;
- 按照邊是否有指向來分類:
有向圖(Directed Graph):在每個邊的定義中,節點都是有序的對。也就是(A,B)與(B,A)表示不同的邊,一個代表從A到B方向的邊,一個代表從B到A方向的邊。無向圖(Undirected Graph):邊只是代表連結,沒有指向性。(A,B)與(B,A)表示的同樣的邊。
- 根據是否在邊上儲存資料分類:
權重圖(Weighted Graph):圖中的邊上附加了權重或值的圖。這些權重表示連線兩個節點之間的距離、代價、容量或其他度量。權重可以是任何數值,通常用於描述節點間的關係特性。
還有很多分類在此不一一羅列。每類圖可能還會有其獨特的一些特徵描述,比如有向圖(Directed Graph)裡面,以某頂點作為開始的邊的數量稱為這個頂點的入度(Indegree),以某個頂點作為結束的邊的數量稱為這個頂點的出度(Outdegree)等等。
通過以上描述,可以感受到圖其實是非常靈活的資料結構,同時它的衍生概念也非常多;初次探究大可不必一一記牢,有個基本的圖結構知識體系即可,後續遇到的時候再擴充圖的知識體系更為合適。
圖的表達(Representation of Graphs)
圖的表達其實也有多種形式,不過最基本的形式是:鄰接矩陣(Adjacency Matrix) 與 鄰接表(Adjacency List)
鄰接矩陣(Adjacency Matrix)
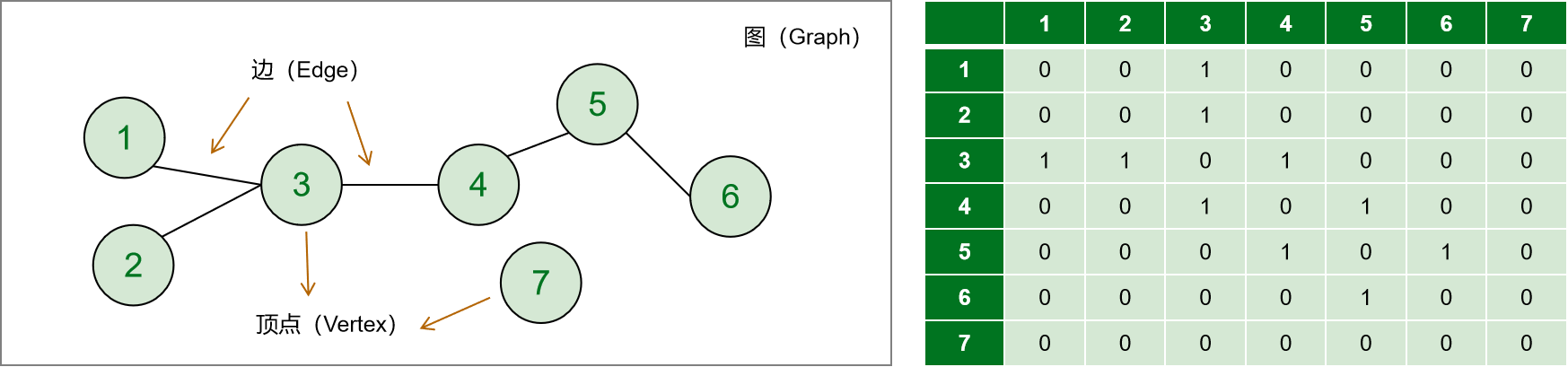
鄰接矩陣,所謂「矩陣」具體到程式碼其實就是二維陣列,通過二維陣列來表示圖中頂點之間的邊的關係。二維陣列中的行和列分別代表圖中的頂點,矩陣中的值表示頂點之間是否相連或連線的邊的權重。
且用這種方式來表示先前範例的圖結構,矩陣的值 0代表無相連邊,1代表有相連邊。如下:
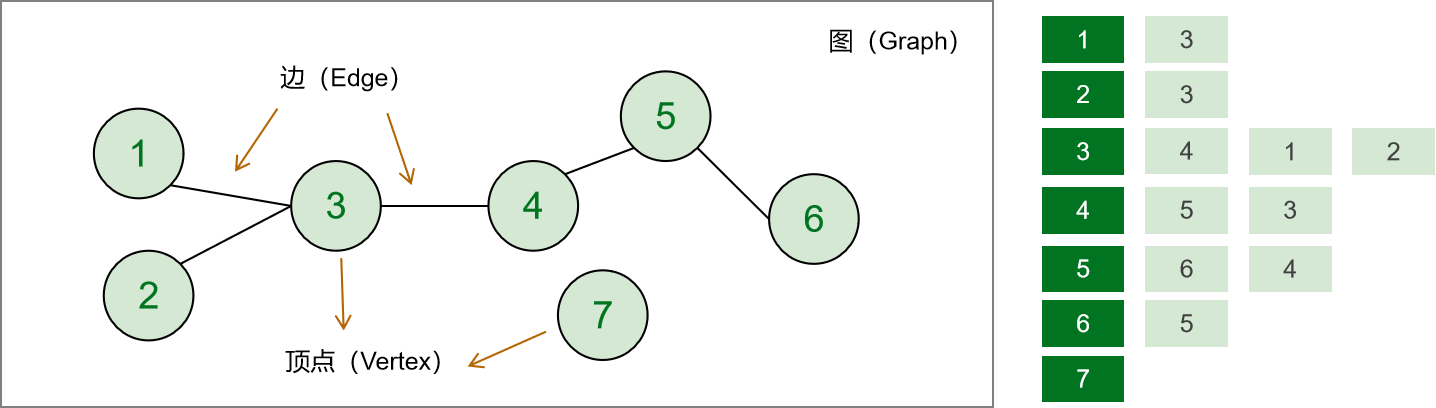
鄰接表(Adjacency List)
鄰接表,所謂「表」指的就是列表 List ,圖中的每個節點都有一個對應的列表,用於儲存與該節點直接相連的其他節點的資訊。鄰接表中的每個節點列表包含了該節點相鄰節點的識別符號或指標等資訊。對於無權圖,通常使用陣列或連結串列來儲存相鄰節點的識別符號。而對於帶權圖,列表中可能還包含了邊的權重資訊。
基本應用範例(Basic Examples)
Leetcode 997. 找到小鎮的法官【簡單】
小鎮裡有 n 個人,按從 1 到 n 的順序編號。傳言稱,這些人中有一個暗地裡是小鎮法官。
如果小鎮法官真的存在,那麼:
小鎮法官不會信任任何人。
每個人(除了小鎮法官)都信任這位小鎮法官。
只有一個人同時滿足屬性 1 和屬性 2 。
給你一個陣列 trust ,其中 trusti = ai, bi 表示編號為 ai 的人信任編號為 bi 的人。
如果小鎮法官存在並且可以確定他的身份,請返回該法官的編號;否則,返回 -1 。
範例
輸入:n = 2, trust = [1,2]
輸出:2
題目故事背景描述比較多,可以看到 信任的表述 可以用有向圖的邊來表示,每個人 用頂點 來表示,小鎮法官的第1點 代表就是出度為 0,第2點 代表就是 入度為 n-1。 這樣題目就轉換為:判斷一個n個頂點的有向圖中 是否存在出度為0,入度為n-1的頂點 ;存在返回頂點編號,不存在返回 -1。
PS:關鍵點,將複雜描述的題目,建模成為圖
public int findJudge(int n, int[][] trust) {
int[] outDegree = new int[n+1],inDegree = new int[n+1];
for(int i = 0; i < trust.length; i++){
outDegree[trust[i][0]] ++;
inDegree[trust[i][1]]++;
}
for(int i=1; i<= n; i++)
if(outDegree[i] == 0 && inDegree[i] == (n-1))
return i;
return -1;
}
Leetcode 787. K 站中轉內最便宜的航班【中等】
有 n 個城市通過一些航班連線。給你一個陣列 flights ,其中 flightsi = fromi, toi, pricei ,表示該航班都從城市 fromi 開始,以價格 pricei 抵達 toi。
現在給定所有的城市和航班,以及出發城市 src 和目的地 dst,你的任務是找到出一條最多經過 k 站中轉的路線,使得從 src 到 dst 的 價格最便宜 ,並返回該價格。 如果不存在這樣的路線,則輸出 -1。
範例
輸入: n = 3, edges = [0,1,100,1,2,100,0,2,500],src = 0, dst = 2, k = 1
輸出: 200
備註:1 <= n <= 100,航班沒有重複,且不存在自環
將城市看作是頂點,城市-城市之間的航班看作是 有向圖邊,航班的價格作為邊的權重,也就完成了題意到圖的建模。考慮到,城市數量 n < 100, 因此可以採用 鄰接矩陣的方式來進行圖的表達。
public int findCheapestPrice(int n, int[][] flights, int src, int dst, int k) {
// 圖 初始化建模
int[][] map = new int[n][n];
for(int i = 0; i < flights.length; i++){
map[flights[i][0]][flights[i][1]] = flights[i][2];
}
// 其他邏輯
}
以 src 作為 源頂點,通過以 src作為 起始頂點的邊 連結到更多的頂點(此時經過 0個站中轉);以這些連結到的頂點 為起始點,繼續連結到更多的頂點(經過 1個站中轉);繼而可以推導到 經過 n 個站中轉。這也就是典型的廣度優先搜尋(BFS),來遍歷以src作為 源頂點的圖,遍歷程式碼如下:
public int findCheapestPrice(int n, int[][] flights, int src, int dst, int k) {
// ...
// BFS
Deque<Integer> que = new ArrayDeque<>();
// src 作為起始點
que.offer(src);
// 經過 k 箇中轉站
for(int i = 0; i <= k && !que.isEmpty(); i++){
int size = que.size();
while( size-- > 0){
int node = que.poll();
for(int j = 0; j < map[node].length; j++){
// map[node][j] == 0 代表 node -> 不相連跳過
if( map[node][j] == 0) continue;
// ... 這裡可以加入遍歷過程中更多的邏輯
// 進入下一輪遍歷
que.offer(j);
}
}
}
// ...
}
考慮題目需要的是 最多經過 k 站中轉的 最便宜線路,不妨 廣度優先遍歷中 用 distSet[] 記錄下 src 可到達站點的 最低價格;最後返回 distSet[ dst ] 即可, 這裡注意下的是 如果沒到達,按照題意應返回 -1。
public int findCheapestPrice(int n, int[][] flights, int src, int dst, int k) {
// ...
int[] distSet = new int[n];
que.offer(src);
for(int i = 0; i <= k && !que.isEmpty(); i++){
// 判斷當前最小的 標準 是基於上一輪的遍歷結果
int[] pre = Arrays.copyOf(distSet,distSet.length);
int size = que.size();
while( size-- > 0){
int node = que.poll();
for(int j = 0; j < map[node].length; j++){
if( map[node][j] == 0) continue;
// distSet[j] == 0 代表之前沒有到達過,因此需要 寫入 distSet[j]
// 如果當前距離 不之前大,這個頂點不必進行下一輪遍歷
if( distSet[j] != 0 &&
distSet[j] < pre[node] + map[node][j]) continue;
// 記錄最小結果
distSet[j] = pre[node] + map[node][j] ;
que.offer(j);
}
}
}
// distSet[j] == 0 代表之前沒有到達過,返回 -1
return distSet[dst] == 0 ? -1:distSet[dst];
}
這裡其實是 使用 Bellman-Ford 演演算法的思想進行解題;在圖演演算法領域還有著很多著名的演演算法,後續可以整理下更專業的解讀,這裡只是演示個簡單的應用。
Bellman-Ford 演演算法,最初由Alfonso Shimbel 1955年提出,但以 Richard Bellman 和 Lester Ford Jr.的名字命名,他們分別於 1958年 和 1956年 發表了該演演算法,向前輩致敬。
最後附上完整程式碼:
public int findCheapestPrice(int n, int[][] flights, int src, int dst, int k) {
int[][] map = new int[n][n];
for(int i = 0; i < flights.length; i++){
map[flights[i][0]][flights[i][1]] = flights[i][2];
}
int[] distSet = new int[n];
Deque<Integer> que = new ArrayDeque<>();
que.offer(src);
for(int i = 0; i <= k && !que.isEmpty(); i++){
int[] pre = Arrays.copyOf(distSet,distSet.length);
int size = que.size();
while( size-- > 0){
int node = que.poll();
for(int j = 0; j < map[node].length; j++){
if( map[node][j] == 0) continue;
if( distSet[j] != 0 &&
distSet[j] < pre[node] + map[node][j]) continue;
distSet[j] = pre[node] + map[node][j] ;
que.offer(j);
}
}
}
return distSet[dst] == 0 ? -1:distSet[dst];
}
歡迎關注 Java研究者 專欄、部落格、公眾號等。大夥兒的喜歡是創作最大的動力。
