[ORB/BEBLID] 利用OpenCV(C++)實現尺度不變性與角度不變性的特徵找圖演演算法

本文只發佈於利用OpenCV實現尺度不變性與角度不變性的特徵找圖演演算法和知乎

一般來說，利用OpenCV實現找圖功能，用的比較多的是模板匹配（matchTemplate）。筆者比較喜歡裡面的NCC演演算法。但是模板有個很明顯的短板，面對尺度改變，角度改變的目標就無能為力了。因此本文旨在做到模板匹配做不到的這兩點上。

當然也有人利用模板匹配實現上面的功能，但是方法之無語，效率之低下讓我不禁想起了三體中的一句話：

「成吉思汗的騎兵，攻擊速度與二十世紀的裝甲部隊相當；北宋的床弩，射程達一千五百米，與二十世紀的狙擊步槍差不多；但這些仍不過是古代的騎兵與弓弩而已，不可能與現代力量抗衡。基礎理論決定一切，未來史學派清楚地看到了這一點。而你們，卻被迴光返照的低階技術矇住了眼睛。你們躺在現代文明的溫床中安於享樂，對即將到來的決定人類命運的終極決戰完全沒有精神上的準備。」

本文並不涉及ORB或者BEBLID演演算法的具體實現，想了解的同學請移步論文。本文撰自一名非計算機系大一新生，有不到處還請見諒。

從特徵匹配開始

特徵匹配首先是需要獲得特徵點。通過特徵檢測演演算法，獲得特徵點後利用匹配器，或是計算漢明距離或是計算餘弦距離，將兩個圖上的點連線在一起。

看筆者往期文章淺談OpenCV的多物件匹配透明影象的實現，以及如何匹配半透明控制元件，在這篇文章中用的是SURF演演算法。但是這個演演算法並不支援角度不變性。

筆者在閱讀OpenCV-mobile的readme的時候意外瞭解到ORB演演算法。簡單查詢一下資料，瞭解到ORB(Oriented FAST and Rotated BRIEF)演演算法滿足以下特點

• 支援尺度不變性和角度不變性
• 速度很快，甚至位元徵匹配(NCC)還快(i9 13900hx)
• 開源，免費，無專利
• 目前最快速穩定的特徵點檢測和提取演演算法

ORB = Oriented FAST（特徵點） + Rotated BRIEF（特徵描述）

From https://zhuanlan.zhihu.com/p/91479558

在2020年提出了一個效果更好也更快的特徵描述演演算法Boosted Efficient Binary Local Image Descriptor（筆者不清楚他演演算法這有沒有專利，但是這個演演算法在nonfree裡，如果需要商業化請慎用，或者替換回BRIEF演演算法）

程式碼實現

cv::Ptr<cv::ORB> orb = cv::ORB::create(nKeypoints); //尋找nKeypoints個特徵點
cv::Ptr<cv::xfeatures2d::BEBLID> beblid = cv::xfeatures2d::BEBLID::create(0.75f, cv::xfeatures2d::BEBLID::SIZE_256_BITS);//用256個位元來描述特徵

std::vector<cv::KeyPoint> src_keypoints, target_keypoints;
cv::Mat src_descriptors, target_descriptors;

orb->detect(src_mat, src_keypoints);
orb->detect(target_mat, target_keypoints);

beblid->compute(src_mat, src_keypoints, src_descriptors);
beblid->compute(target_mat, target_keypoints, target_descriptors);

cv::BFMatcher matcher(cv::NORM_HAMMING, true);//利用漢明距離的匹配器

std::vector<cv::DMatch> matches;
matcher.match(target_descriptors, src_descriptors, matches);

std::vector<cv::Point2d> matched_target, matched_src;
for(auto &match : matches)
{
    if(match.distance > max_distance)
        break;
    
	matched_target.push_back(target_keypoints[match.queryIdx].pt);
	matched_src.push_back(src_keypoints[match.trainIdx].pt);
}

這裡建立了ORB和BEBLID物件，並且對目標圖片完成了匹配，將彼此能夠匹配的點對應存放到了matched_target和matched_src裡。

從透視變換繼續

雖然我們這裡成功建立了模板圖和目標圖的特徵對等關係，然而，很多時候我們想要的是特徵匹配提供的那種更為直接的反映在目標圖裡的座標。

如何將離散的的點集轉換為模板在目標圖上的大致區域，成了我們需要解決的一個問題。這裡我使用的方法是findHomography和perspectiveTransform。

• findHomography 計算多個二維點對之間的最優單對映變換矩陣H(3行3列)。使用最小均方誤差或RANSAC方法。比較好解釋的是最小均方誤差方法，但是為了效果筆者用的是RANSAC方法。關於這個矩陣作用，大家可以去B站上看3blue1brown的系列視訊《線性代數的本質》。我們獲取到這個矩陣，就可以估計出模板圖怎麼變化到目標圖上。同理模板的四個角的座標也可以通過這個矩陣變換到目標圖上的座標，就得到了模板在目標圖上的大致位置和邊界。

• perspectiveTransform 透視變換，就是完成座標的變換過程。

程式碼實現

cv::Mat H = cv::findHomography(matched_src, matched_target, cv::RANSAC);

std::vector<cv::Point2f> obj_corners(4);
obj_corners[0] = cv::Point2f(0, 0);
obj_corners[1] = cv::Point2f((float)target_mat.cols, 0);
obj_corners[2] = cv::Point2f((float)target_mat.cols, (float)target_mat.rows);
obj_corners[3] = cv::Point2f(0, (float)target_mat.rows);

std::vector<cv::Point2f> buf_corners(4);

cv::perspectiveTransform(obj_corners, buf_corners, H);

效果展示

縮放	壓扁	旋轉

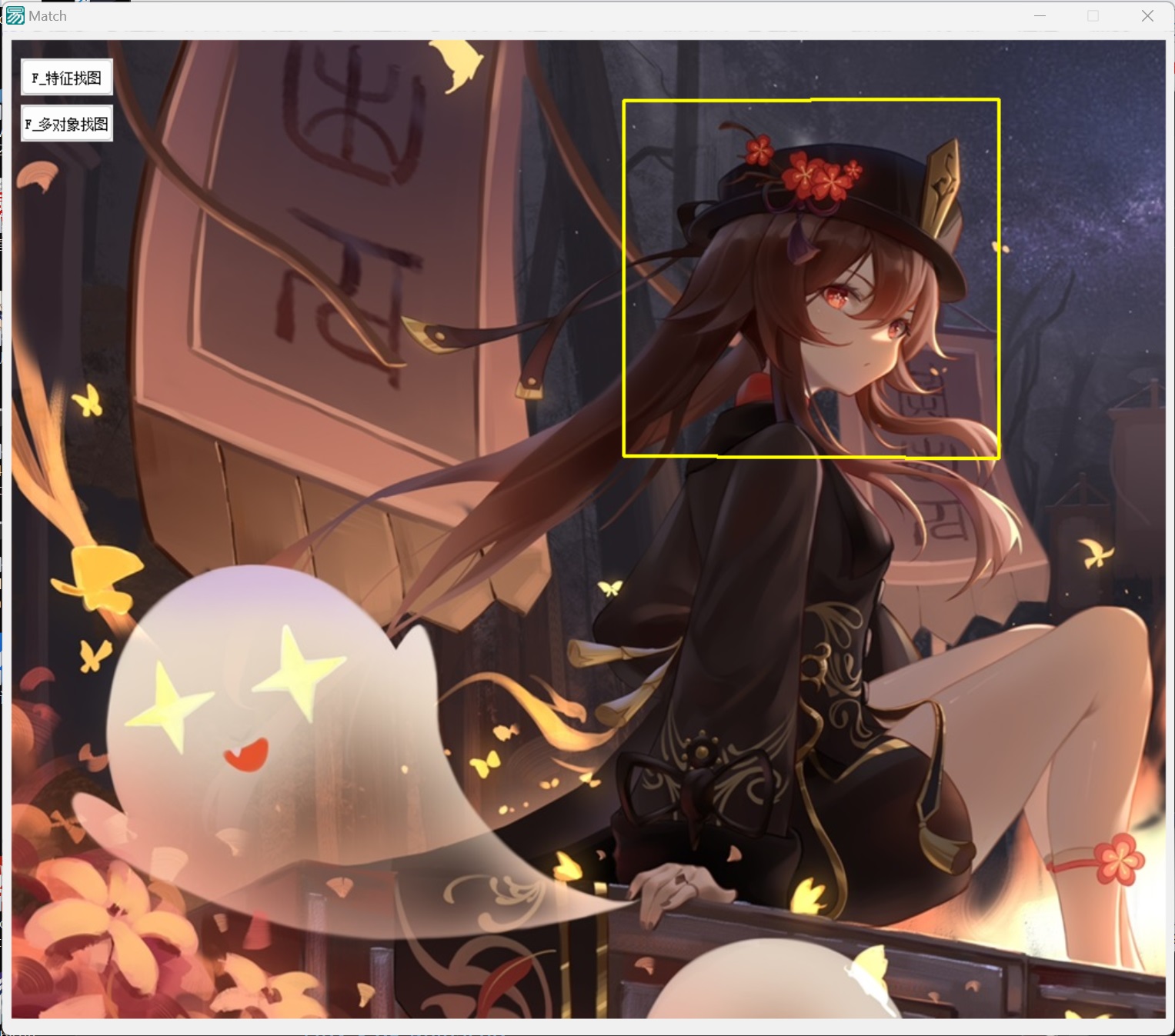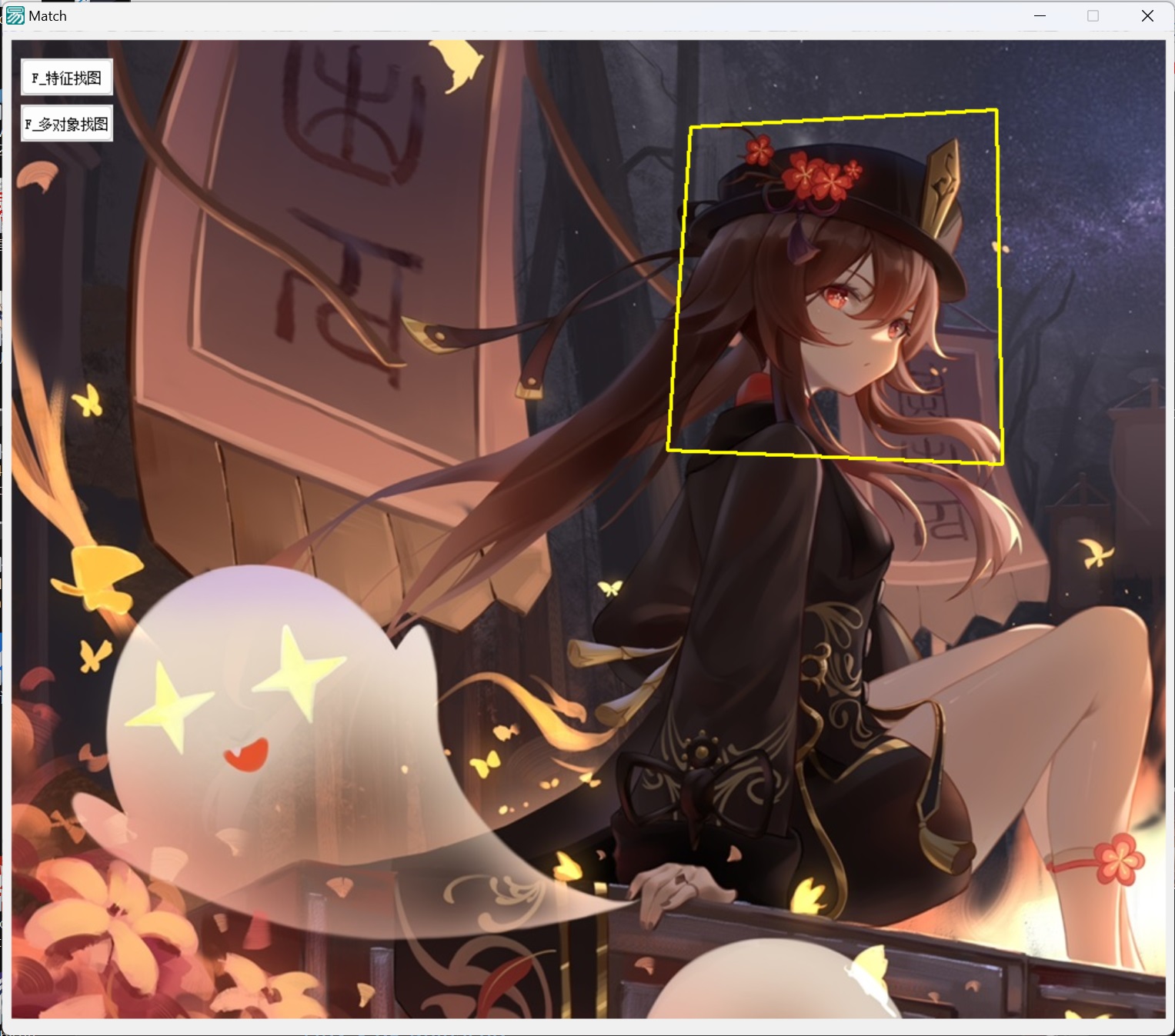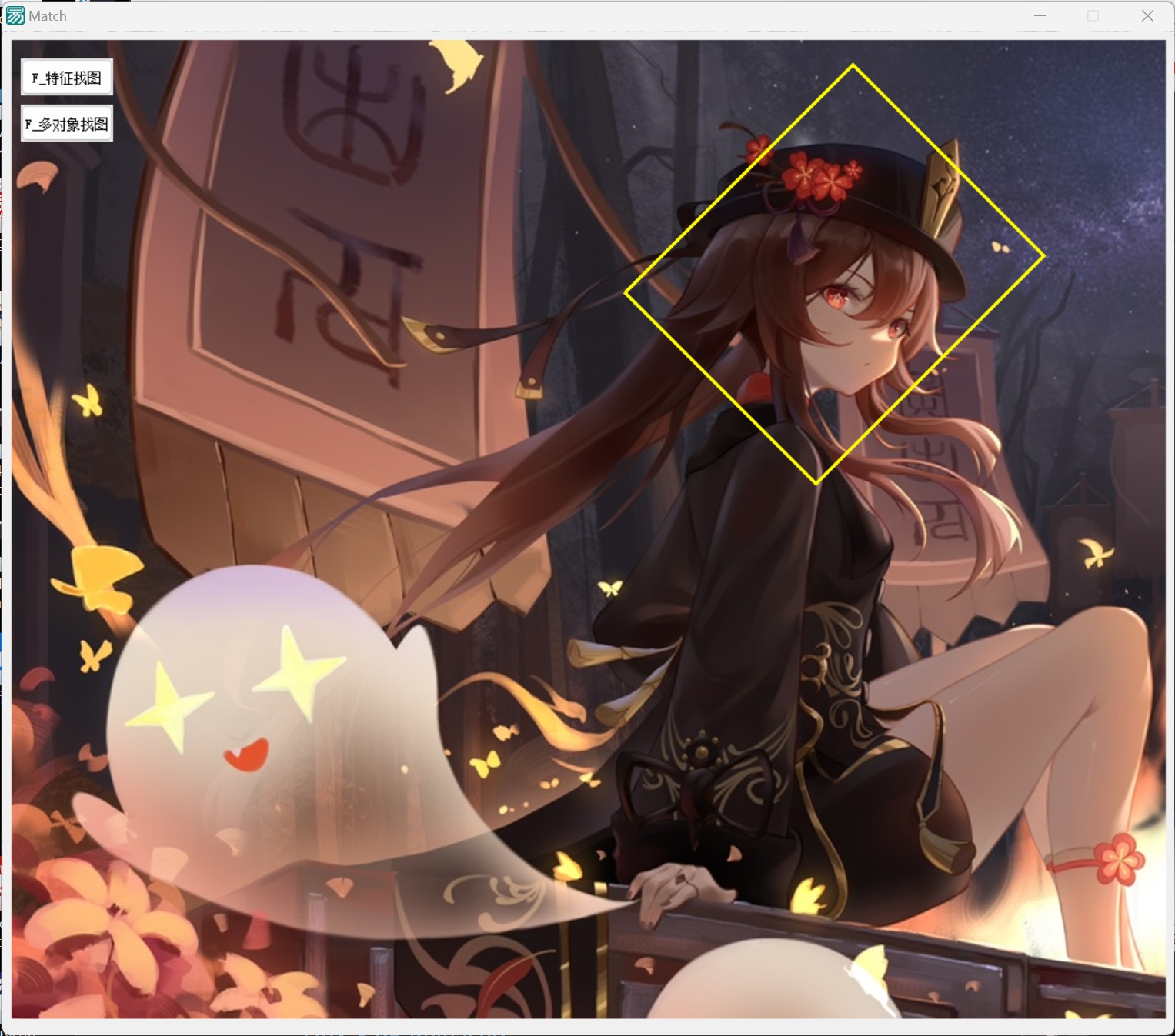可以發現實現的效果非常好。

還能更強？

這裡只實現了單個目標的檢測匹配，事實上這個演演算法不止步於此，我們可以使用KMeans演演算法，實現對於一個圖片上多個目標一次檢測。也可以多個圖片同時匹配。但是鑑於時間，和筆者不容樂觀的數學分析成績，以及即將到來的數論期中考試，為了不被踢出強基計劃，下次有時間再說吧。