NEFU OJ Problem1485 貪吃蛇大作戰題解

Problem:F
Time Limit:1000ms
Memory Limit:65535K

題目

Description

貪吃蛇大家一定都玩過吧，現在宋哥也要玩這個遊戲，最初的時候貪吃蛇從螢幕的左下角出發，但是有一個非常不幸的事情，就是宋哥的遊戲機的左鍵和下鍵壞掉了，這意味著什麼？沒錯！他只能操控他的蛇向右或向上走了，假設螢幕被劃分為10^9*109的格子，而貪吃蛇從座標為(1,1)的格子出發，每次操作可以從座標為(x,y)的格子前往座標為(x+1,y)或(x,y+1)的格子，在所有格子中有一些格子中有一些食物，宋哥現在想知道，他的貪吃蛇最多能吃到多少食物呢？

Input

輸入的第一行包含一個數位T(1<=T<=10)，代表資料組數，之後的每組資料的每一行包含一個數位n (1<=n<=1000)，代表有食物的格子數量，之後的n行每一行包含三個數位xi(1<=xi<=10^{9),yi(1<=xi<=10}9),pi(1<=xi<=10^6)，分別代表格子的座標和在這個格子裡的食物數量。

Output

輸出T行，第i行為第i組資料的答案。

Sample Input

2
3
1 1 1
2 2 2
3 3 3
3
1 3 1
2 2 2
3 1 3

Sample Output

6
3

Hint

Source

MGH

思路

看起來像很經典的dp問題，但是區別是點很稀疏，只有1e3的點，卻有1e9*1e9的棋盤，考慮將點位置重新緊密排布, 建立一個對映將稀疏點集\(S\)對映到緊密點集\(P'\)即 \(f:\{P_i = (X_i,Y_i)\in S\}\rightarrow \{P'_i=(X'_i,Y'_i)\in S'\}\)使得\(S'\)方便使用dp。

需要保證重新排布後性質不變，分析後得知需要滿足保持原本的橫縱座標的大小關係即

\[\forall P_i, P_j\in S \left\{ \begin{array}{c} x_i < x_j \rightarrow x'_i < x'_j\\ x_i = x_j \rightarrow x'_i = x'_j\\ x_i > x_j \rightarrow x'_i > x'_j\\ \end{array} \right. \]

\[\forall P_i, P_j\in S \left\{ \begin{array}{c} y_i < y_j \rightarrow y'_i < y'_j\\ y_i = y_j \rightarrow y'_i = y'_j\\ y_i > y_j \rightarrow y'_i > y'_j\\ \end{array} \right. \]

如下圖所示方法，刪除所有空行和空列可以實現。

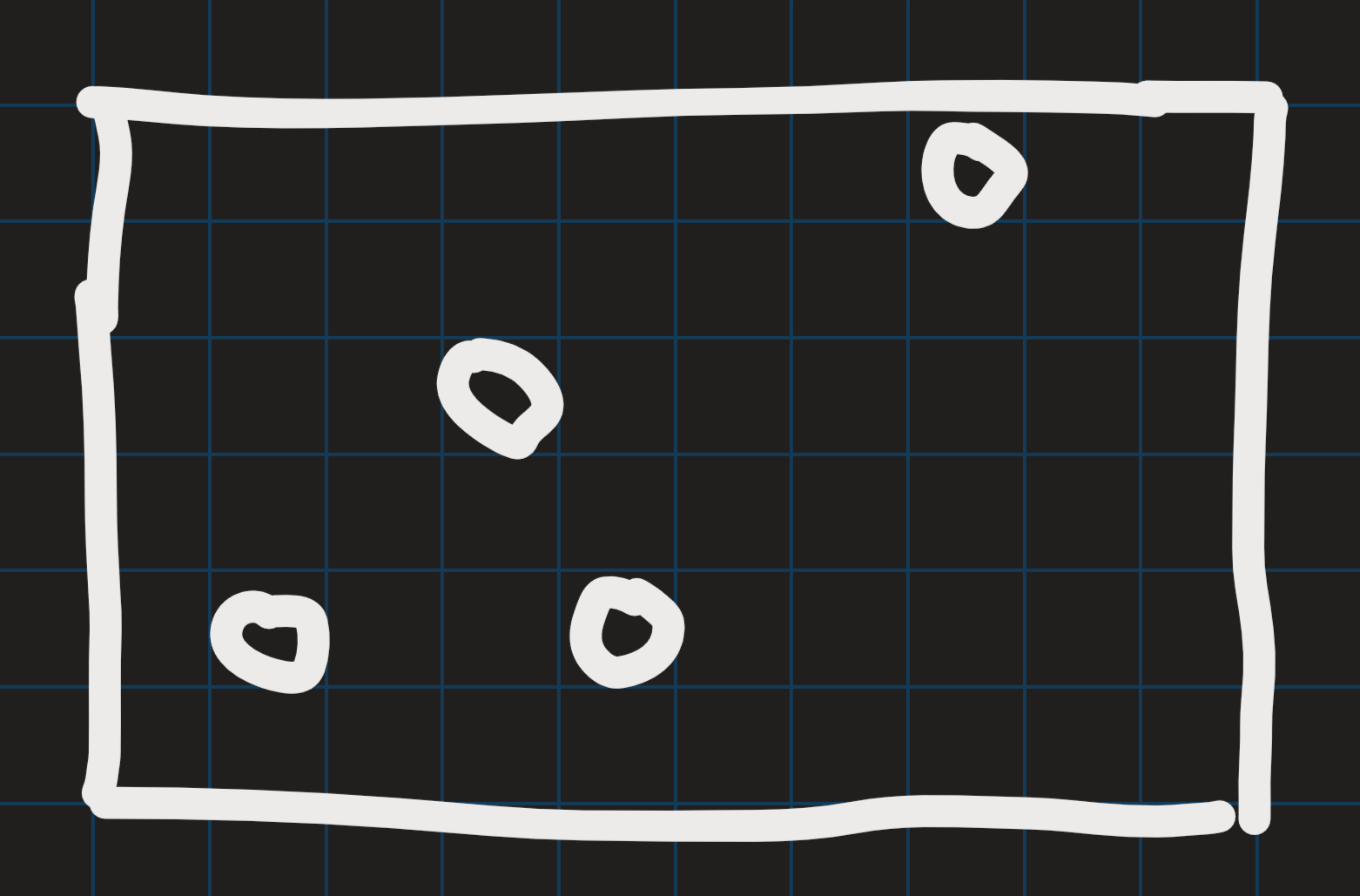
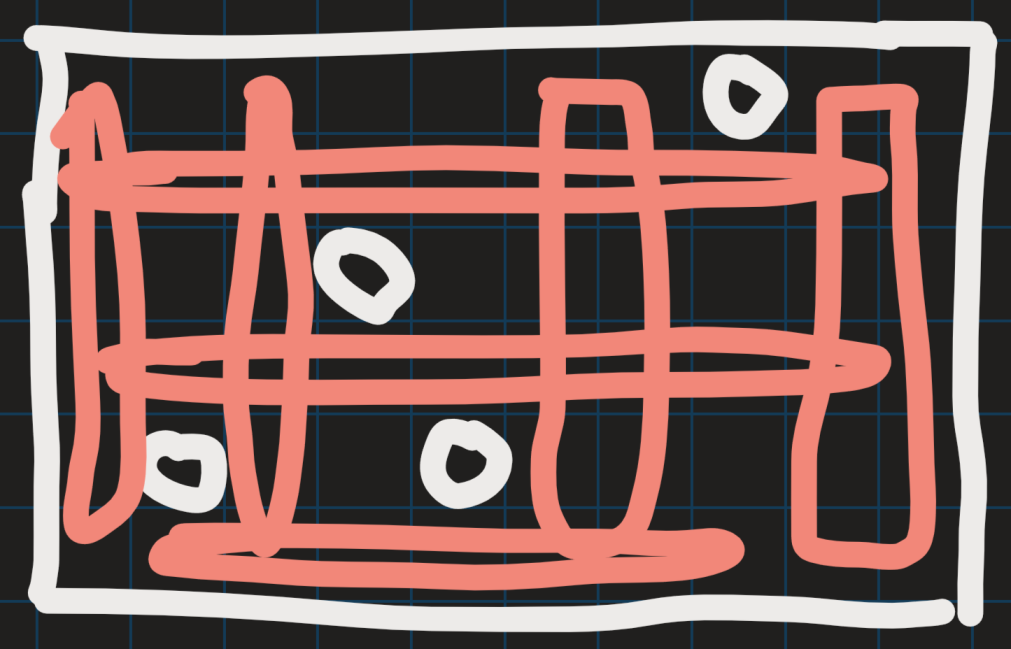
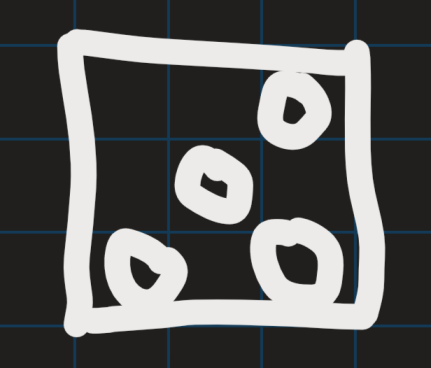
演演算法實現

對\(x\)座標由小到大排序
對於每個點遍歷從0開始分配新的\(x'\)座標，如果某個點\(x\)座標與上一個點相同，則分配相同的\(x'\)座標，而不遞增\(x'\)。

之後再對\(y\)座標進行同樣的操作。

完成後對\(S'\)點集進行DP即可

程式碼如下

#include <bits/stdc++.h>

using namespace std;

struct Food
{
    int x, y, v, _x, _y;//_x和_y代表對映後坐標
} food[1020];

int mp[1020][1020], dp[1020][1020];

bool Cmp1(Food f1, Food f2)//x排序
{
    return f1.x < f2.x;
}
bool Cmp2(Food f1, Food f2)//y排序
{
    return f1.y < f2.y;
}

int Find(int x, int y)//Dp
{
    if(dp[x][y] != -1)
        return dp[x][y];

    int res = 0;
    if(x-1 >= 0)
        res = max(res, Find(x-1,y));
    if(y-1 >= 0)
        res = max(res, Find(x,y-1));
    return dp[x][y] = res + mp[x][y];
}
int main()
{
    int T;
    cin >> T;
    while(T--)
    {
        int n;
        cin >> n;
        for (int i = 0; i < n; i ++)
            scanf("%d%d%d", &food[i].x, &food[i].y, &food[i].v);

        //x排序並分配新座標
        sort(food, food+n, Cmp1);
        int ind_x = 1;
        food[0]._x = 1;
        for (int i = 1; i < n; i ++)
            if(food[i].x == food[i-1].x)
                food[i]._x = ind_x;
            else
                food[i]._x = ++ind_x;

        //y排序並分配新座標
        sort(food, food+n, Cmp2);
        int ind_y = 1;
        food[0]._y = 1;
        for (int i = 1; i < n; i ++)
            if(food[i].y == food[i-1].y)
                food[i]._y = ind_y;
            else
                food[i]._y = ++ind_y;


        //普通DP過程
        for (int i = 0; i <= 1000; i ++)
            for (int j = 0; j <= 1000; j ++)
                mp[i][j] = 0;

        for (int i = 0; i < n; i ++)
            mp[food[i]._x][food[i]._y] = food[i].v;

        for (int i = 0; i <= ind_x; i ++)
            for (int j = 0; j <= ind_y; j ++)
                dp[i][j] = -1;

        dp[0][0] = 0;

        cout << Find(ind_x,ind_y) << endl;
    }
    return 0;
}

NEFU OJ Problem1485 貪吃蛇大作戰 題解

題目