本篇文章全面深入地探討了支援向量機（SVM）的各個方面，從基本概念、數學背景到Python和PyTorch的程式碼實現。文章還涵蓋了SVM在文字分類、影象識別、生物資訊學、金融預測等多個實際應用場景中的用法。

關注TechLead，分享AI全維度知識。作者擁有10+年網際網路服務架構、AI產品研發經驗、團隊管理經驗，同濟本復旦碩，復旦機器人智慧實驗室成員，阿里雲認證的資深架構師，專案管理專業人士，上億營收AI產品研發負責人。

一、引言

背景

支援向量機（SVM, Support Vector Machines）是一種廣泛應用於分類、迴歸、甚至是異常檢測的監督學習演演算法。自從Vapnik和Chervonenkis在1995年首次提出，SVM演演算法就在機器學習領域贏得了巨大的聲譽。這部分因為其基於幾何和統計理論的堅實數學基礎，也因為其在實際應用中展示出的出色效能。

例子：比如，在臉部辨識或者文字分類問題上，SVM常常能夠實現優於其他演演算法的準確性。

SVM演演算法的重要性

SVM通過尋找能夠最大化兩個類別間「間隔」的決策邊界（或稱為「超平面」）來工作，這使得其在高維空間中具有良好的泛化能力。

例子：在垃圾郵件分類問題中，可能有數十甚至數百個特徵，SVM能有效地在這高維特徵空間中找到最優決策邊界。

二、SVM基礎

線性分類器簡介

支援向量機（SVM）屬於線性分類器的一種，旨在通過一個決策邊界將不同的資料點分開。在二維平面中，這個決策邊界是一條直線；在三維空間中是一個平面，以此類推，在N維空間，這個決策邊界被稱為「超平面」。

例子: 在二維平面上有紅色和藍色的點，線性分類器（如SVM）會尋找一條直線，儘量使得紅色點和藍色點被分開。

什麼是支援向量？

在SVM演演算法中，"支援向量"是指距離超平面最近的那些資料點。這些資料點被用於確定超平面的位置和方向，因為它們最有可能是分類錯誤的點。

例子: 在一個用於區分貓和狗的分類問題中，支援向量可能是一些極易被誤分類的貓或狗的圖片，例如長得像貓的狗或者長得像狗的貓。

超平面和決策邊界

超平面是SVM用來進行資料分類的決策邊界。在二維空間裡，超平面就是一條直線；在三維空間裡是一個平面，以此類推。數學上，一個N維的超平面可以表示為(Ax + By + ... + Z = 0)的形式。

例子: 在一個文字分類問題中，你可能使用詞頻和其他文字特徵作為維度，超平面就是在這個多維空間裡劃分不同類別（如垃圾郵件和非垃圾郵件）的決策邊界。

SVM的目標函數

SVM的主要目標是找到一個能「最大化」支援向量到超平面距離的超平面。數學上，這被稱為「最大化間隔」。目標函數通常是一個凸優化問題，可通過各種演演算法（如梯度下降、SMO演演算法等）求解。

例子: 在信用卡欺詐檢測系統中，SVM的目標是找到一個能最大化「良性」交易和「欺詐」交易之間間隔的超平面，以便能更準確地分類新的交易記錄。

三、數學背景和優化

拉格朗日乘子法（Lagrange Multipliers）

拉格朗日乘子法是一種用於求解約束優化問題的數學方法，特別適用於支援向量機（SVM）中的優化問題。基礎形式的拉格朗日函數（Lagrangian Function）可以表示為：

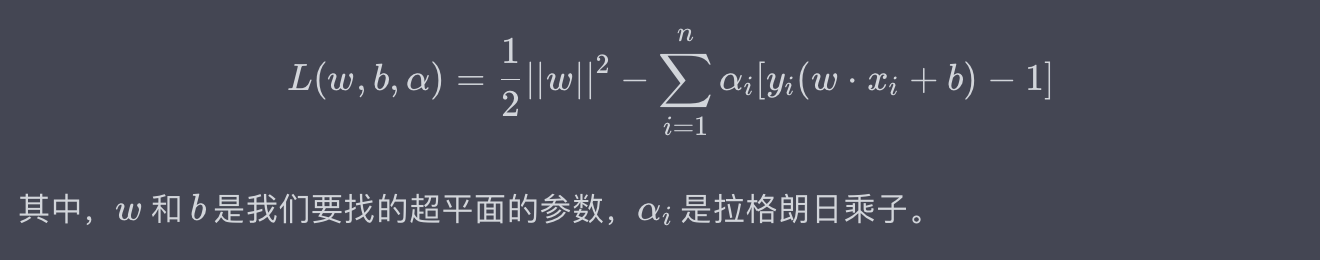
例子：在一個二分類問題中，你可能需要最小化(w) 的範數（即，優化模型的複雜度）的同時，確保所有的樣本都被正確分類（或儘可能地接近這個目標）。拉格朗日乘子法正是解決這種問題的一種方法。

KKT條件

Karush-Kuhn-Tucker（KKT）條件是非線性規劃問題中的一組必要條件，也用於SVM中的優化問題。它是拉格朗日乘子法的一種擴充套件，用於處理不等式約束。在SVM中，KKT條件主要用來檢驗一個給定的解是否是最優解。

例子：在SVM模型中，KKT條件能幫助我們驗證找到的超平面是否是最大化間隔的超平面，從而確認模型的優越性。

核技巧（Kernel Trick）

核技巧是一種在高維空間中隱式計算資料點之間相似度的方法，而無需實際進行高維計算。這讓SVM能夠有效地解決非線性問題。常用的核函數包括線性核、多項式核、徑向基核（RBF）等。

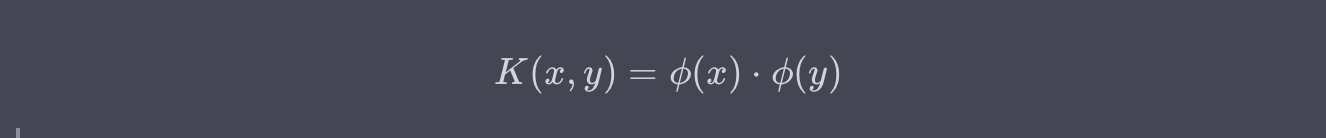
例子：如果你在一個文字分類任務中遇到了非線性可分的資料，使用核技巧可以在高維空間中找到一個能夠將資料有效分開的決策邊界。

雙重問題和主問題（Dual and Primal Problems）

在SVM中，優化問題通常可以轉換為其對偶問題，這樣做的好處是對偶問題往往更容易求解，並且能更自然地引入核函數。雙重問題與主問題通過所謂的對偶間隙（duality gap）聯絡在一起，而當對偶間隙為0時，雙重問題的解即為主問題的解。

例子：在處理大規模資料集時，通過解決雙重問題而不是主問題，可以大大減少計算複雜性和時間。

四、程式碼實現

在這一部分中，我們將使用Python和PyTorch庫來實現一個基礎的支援向量機（SVM）。我們會遵循以下幾個主要步驟：

資料預處理：準備用於訓練和測試的資料。
模型定義：定義SVM模型的架構。
優化器選擇：選擇合適的優化演演算法。
訓練模型：使用訓練資料來訓練模型。
評估模型：使用測試資料來評估模型的效能。

資料預處理

首先，我們需要準備一些用於訓練和測試的資料。為簡單起見，我們使用PyTorch內建的Tensor資料結構。

import torch

# 建立訓練資料和標籤
X_train = torch.FloatTensor([[1, 1], [1, 2], [1, 3], [2, 1], [2, 2], [2, 3]])
y_train = torch.FloatTensor([1, 1, 1, -1, -1, -1])

# 建立測試資料
X_test = torch.FloatTensor([[1, 0.5], [2, 0.5]])

例子: X_train 中的資料表示二維平面上的點，而 y_train 中的資料則代表這些點的標籤。例如，點 (1, 1) 的標籤是 1，而點 (2, 3) 的標籤是 -1。

模型定義

下面我們定義SVM模型。在這裡，我們使用線性核函數。

class LinearSVM(torch.nn.Module):
    def __init__(self):
        super(LinearSVM, self).__init__()
        self.weight = torch.nn.Parameter(torch.rand(2), requires_grad=True)
        self.bias = torch.nn.Parameter(torch.rand(1), requires_grad=True)
    
    def forward(self, x):
        return torch.matmul(x, self.weight) + self.bias

例子: 在這個例子中，我們定義了一個線性SVM模型。self.weight 和 self.bias 是模型的引數，它們在訓練過程中會被優化。

優化器選擇

我們將使用PyTorch的內建SGD（隨機梯度下降）作為優化器。

# 範例化模型和優化器
model = LinearSVM()
optimizer = torch.optim.SGD([model.weight, model.bias], lr=0.01)

訓練模型

下面的程式碼段展示瞭如何訓練模型：

# 設定訓練輪次和正則化引數C
epochs = 100
C = 0.1

for epoch in range(epochs):
    for i, x in enumerate(X_train):
        y = y_train[i]
        optimizer.zero_grad()
        
        # 計算間隔損失 hinge loss: max(0, 1 - y*(wx + b))
        loss = torch.max(torch.tensor(0), 1 - y * model(x))
        
        # 新增正則化項: C * ||w||^2
        loss += C * torch.norm(model.weight)**2
        
        loss.backward()
        optimizer.step()

例子: 在這個例子中，我們使用了hinge loss作為損失函數，並新增了正則化項C * ||w||^2以防止過擬合。

評估模型

最後，我們使用測試資料來評估模型的效能。

with torch.no_grad():
    for x in X_test:
        prediction = model(x)
        print(f"Prediction for {x} is: {prediction}")

例子: 輸出的「Prediction」表示模型對測試資料點的分類預測。一個正數表示類別 1，一個負數表示類別 -1。

五、實戰應用

支援向量機（SVM）在各種實際應用場景中都有廣泛的用途。

文字分類

在文字分類任務中，SVM可以用來自動地對檔案或訊息進行分類。例如，垃圾郵件過濾器可能使用SVM來識別垃圾郵件和正常郵件。

例子: 在一個新聞網站上，可以使用SVM模型來自動將新聞文章分為「政治」、「體育」、「娛樂」等不同的類別。

影象識別

SVM也被用於影象識別任務，如手寫數位識別或面部識別。通過使用不同的核函數，SVM能夠在高維空間中找到決策邊界。

例子: 在安全監控系統中，SVM可以用於識別不同的人臉並進行身份驗證。

生物資訊學

在生物資訊學領域，SVM用於識別基因序列模式，以及用於藥物發現等多個方面。

例子: 在疾病診斷中，SVM可以用於分析基因表達資料，以識別是否存在特定疾病的風險。

金融預測

SVM在金融領域也有一系列應用，如用於預測股票價格的走勢或者用於信用評分。

例子: 在信用卡欺詐檢測中，SVM可以用於分析消費者的交易記錄，並自動標識出可能的欺詐性交易。

客戶細分

在市場分析中，SVM可以用於客戶細分，通過分析客戶的購買歷史、地理位置等資訊，來預測客戶的未來行為。

例子: 在電子商務平臺上，SVM模型可以用於預測哪些客戶更有可能購買特定的產品。

六、總結

支援向量機（SVM）是一種強大而靈活的機器學習演演算法，具有廣泛的應用場景和優秀的效能表現。從文字分類到影象識別，從生物資訊學到金融預測，SVM都表現出其強大的泛化能力。在這篇文章中，我們不僅介紹了SVM的基本概念、數學背景和優化方法，還通過具體的Python和PyTorch程式碼實現了一個基礎的SVM模型。此外，我們還探討了SVM在多個實際應用場景中的用法。

雖然SVM被廣泛應用於各種問題，但它並非「一把通吃」的工具。在高維空間和巨量資料集上，SVM模型可能會遇到計算複雜性和記憶體使用的問題。此時，適當的核函數選擇、資料預處理和引數優化尤為重要。

值得注意的是，隨著深度學習的興起，一些更為複雜的模型（如神經網路）在某些特定任務上可能會表現得更好。然而，SVM因其解釋性強、理論基礎堅實而依然保有一席之地。實際上，在某些應用場景下，如小資料集或者對模型可解釋性有高要求的情境，SVM可能是更好的選擇。

關注TechLead，分享AI全維度知識。作者擁有10+年網際網路服務架構、AI產品研發經驗、團隊管理經驗，同濟本復旦碩，復旦機器人智慧實驗室成員，阿里雲認證的資深架構師，專案管理專業人士，上億營收AI產品研發負責人。
如有幫助，請多關注
TeahLead KrisChang，10+年的網際網路和人工智慧從業經驗，10年+技術和業務團隊管理經驗，同濟軟體工程本科，復旦工程管理碩士，阿里雲認證雲服務資深架構師，上億營收AI產品業務負責人。

支援向量機SVM：從數學原理到實際應用