【scipy 基礎】--正交距離迴歸
Scipy的ODR正交距離迴歸(ODR-Orthogonal Distance Regression)模組,適用於迴歸分析時,因變數和自變數之間存在非線性關係的情況。
它提高了迴歸分析的準確性和穩健性。對於需要解決非線性迴歸問題的科研人員和工程師來說,它具有非常重要的意義。
ODR正交距離迴歸模組的作用主要在於它將正交化方法和距離迴歸結合起來,解決了傳統線性迴歸模型在處理非線性問題時的侷限性。它通過將自變數進行正交化處理,使得因變數和自變數之間的非線性關係能夠更好地被擬合出來。
1. 主要功能
scipy.odr模組針對的領域比較明確,所以不像之前介紹的模組有那麼多函數。
此模組的主要函數包括:
| 函數名 | 說明 |
|---|---|
| Data | 要擬合的資料 |
| RealData | 資料的權重為實際標準差和/或協方差 |
| Model | Model 類儲存有關您希望擬合的函數的資訊 |
| ODR | ODR 類收集所有資訊並協調主要擬合例程的執行 |
| Output | 輸出類儲存 ODR 執行的輸出 |
| 其他函數 | 調整擬合和模型的一些函數 |
一般來說,使用前5個函數,就可以進行一些正交距離迴歸分析。
2. 使用範例
正交距離分析一般步驟如下:
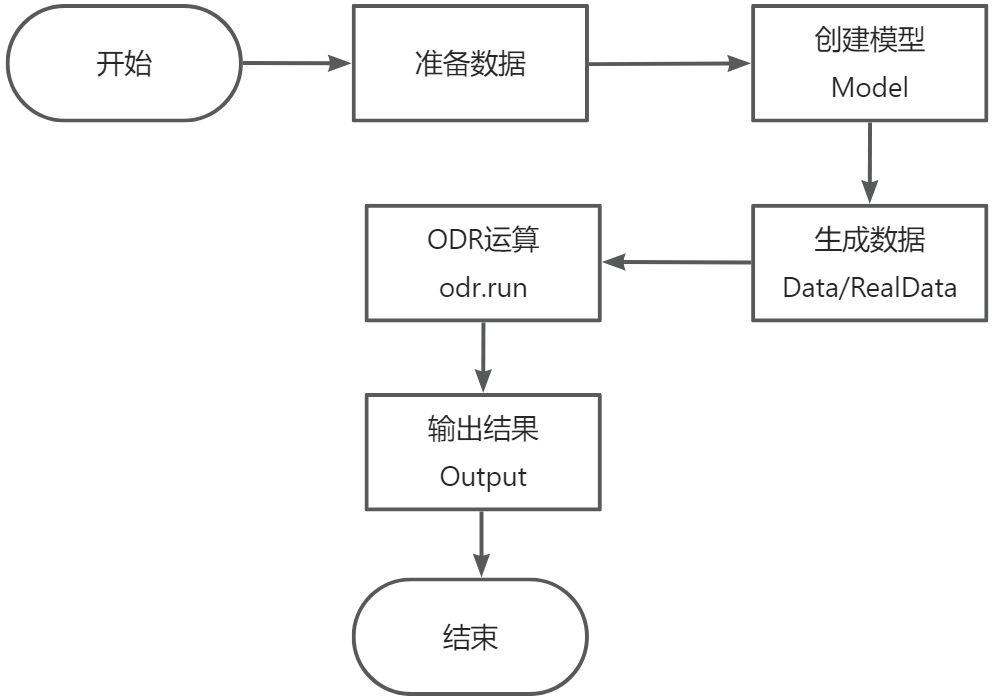
2.1. 準備資料
資料採用以前收集的江蘇省人口資料,獲取地址:https://databook.top/jiangsustat/renkou
import pandas as pd
data = pd.read_csv("/path/to/人口-年末常住人口(萬人).csv")
data.head(10)
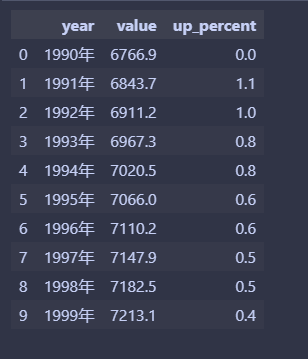
一共31條資料,1990年~2020年江蘇省的人口變化資料。
用散點圖看看資料的變化趨勢:
from matplotlib.ticker import MultipleLocator
import matplotlib.pyplot as plt
ax = plt.subplot()
ax.scatter(data["year"], data["value"], marker='*', color='r')
ax.xaxis.set_major_locator(MultipleLocator(5))
ax.set_title("江蘇省人口變化")
plt.show()
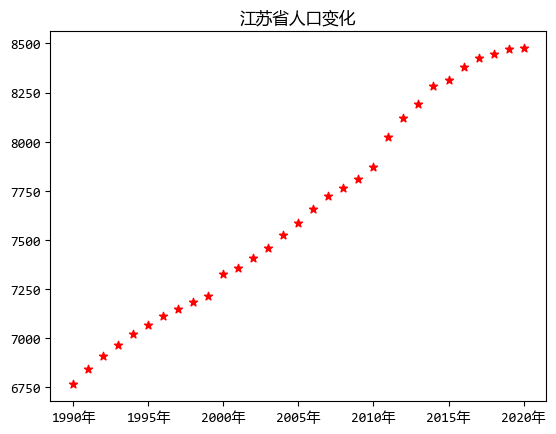
2.2. 建立模型
使用scipy.odr模組中的Model函數建立一個擬合的模型。
import scipy.odr as sodr
# 模型函數
def model_func(p, x):
k, b = p
return k * x + b
model = sodr.Model(model_func)
2.3. 生成資料
將上面的人口資料data轉換為可以用於ODR運算的資料。
# x是資料
x = range(len(data))
# 轉換資料用RealData或者Data函數都可以
rdata = sodr.RealData(x, data["value"])
# rdata = sodr.Data(x, data["value"])
Data和RealData函數都是用來構造資料的。
一般來說,Data函數用來構造理論資料;RealData函數用來構造實際資料的,且RealData中還可以設定權重。
這裡沒有設定權重,用哪個函數都可以。
2.4. ODR運算
有了資料和模型之後,就可以進行ODR運算了。
odr = sodr.ODR(rdata, model, beta0=[0, 1])
result = odr.run()
result.pprint()
# 執行結果:
Beta: [ 61.01340781 6724.77566283]
Beta Std Error: [ 1.11208495 19.3974215 ]
Beta Covariance: [[ 1.51592414 -22.73886321]
[-22.73886321 461.20026764]]
Residual Variance: 0.8158277156001223
Inverse Condition #: 0.2520617152422754
Reason(s) for Halting:
Sum of squares convergence
其中 Beta 和 Beta Std Error就擬合的引數值和引數的標準差。
2.5. 輸出結果
根據計算結果,繪製出圖形更容易理解。
# 擬合引數和引數的標準差
beta = result.beta
beta_std = result.sd_beta
# 擬合的曲線
y = beta[0] * x + beta[1]
# 擬合曲線的標準差上限
y_up = (beta[0] + beta_std[0]) * x + (beta[1]+ beta_std[1])
# 擬合曲線的標準差下限
y_down = (beta[0] - beta_std[0]) * x + (beta[1] - beta_std[1])
# 繪製擬合的曲線
ax = plt.subplot()
ax.scatter(data["year"], data["value"], marker='*', color='r')
ax.xaxis.set_major_locator(MultipleLocator(5))
ax.set_title("江蘇省人口變化")
ax.plot(x, y, color="b", label="擬合曲線")
ax.plot(x, y_up, color="y", label="標準差上限")
ax.plot(x, y_down, color="g", label="標準差下限")
plt.legend()
plt.show()
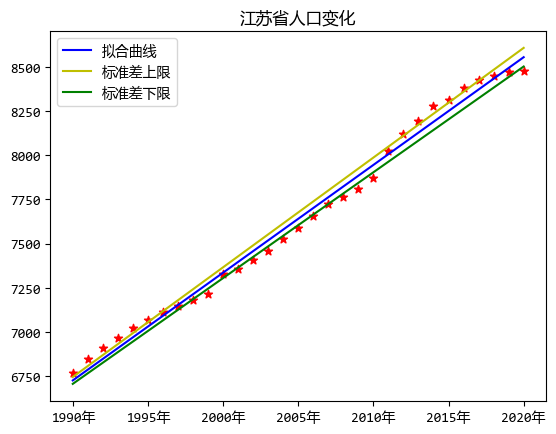
這就是通過ODR模組擬合的人口變化情況。
3. 總結
ODR正交距離迴歸之所以作為Scipy的單獨模組,是因為它是一種特殊的曲線擬合方法,
它使用正交化和距離加權的最小二乘法來處理具有非線性關係的輸入變數,並旨在找到最優的模型以最小化預測誤差。
這與一般的曲線擬合在方法和目標上有很大的不同。
後續介紹Scipy庫中的其他模組時,還會介紹其他的曲線擬合函數,到時候可以和這裡的ODR方法對照比較一下。