KMeans演演算法全面解析與應用案例
本文深入探討了KMeans聚類演演算法的核心原理、實際應用、優缺點以及在文字聚類中的特殊用途,為您在聚類分析和自然語言處理方面提供有價值的見解和指導。
關注TechLead,分享AI全維度知識。作者擁有10+年網際網路服務架構、AI產品研發經驗、團隊管理經驗,同濟本復旦碩,復旦機器人智慧實驗室成員,阿里雲認證的資深架構師,專案管理專業人士,上億營收AI產品研發負責人。
一、聚類與KMeans介紹
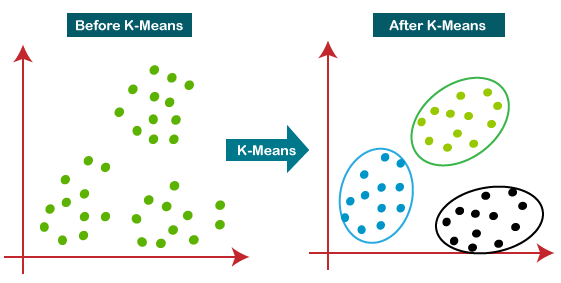
聚類演演算法在機器學習和資料探勘中佔有重要的地位,它們用於自動地將資料分組成有意義的叢集。KMeans聚類演演算法是其中最簡單、最常用的一種。在本篇文章中,我們將深入探討KMeans聚類演演算法的原理、優缺點、變體和實際應用。首先,讓我們瞭解一下聚類和KMeans演演算法的基礎概念。
聚類的基礎概念
定義:聚類是一種無監督學習方法,用於將資料點分組成若干個叢集,以便資料點在同一個叢集內相似度高,而在不同叢集間相似度低。
例子:考慮一個電子商務網站,有數萬名使用者和數千種商品。通過聚類演演算法,我們可以將使用者分為幾個不同的叢集(例如,家庭主婦、學生、職業人士等),以便進行更精準的推薦和行銷。
KMeans演演算法的重要性
定義:KMeans是一種分割區方法,通過迭代地分配每個資料點到最近的一個預定數量(K)的中心點(也稱為「質心」)並更新這些中心點,從而達到劃分資料集的目的。
例子:在社群網路分析中,我們可能想要了解哪些使用者經常互動,形成一個社群。通過KMeans演演算法,我們可以找到這些社群的「中心使用者」,並圍繞他們形成不同的使用者叢集。
這兩個基礎概念為我們後續的深入分析和程式碼實現提供了堅實的基礎。通過理解聚類的目的和KMeans演演算法的工作原理,我們能更好地把握該演演算法在複雜資料分析任務中的應用。
二、KMeans演演算法原理
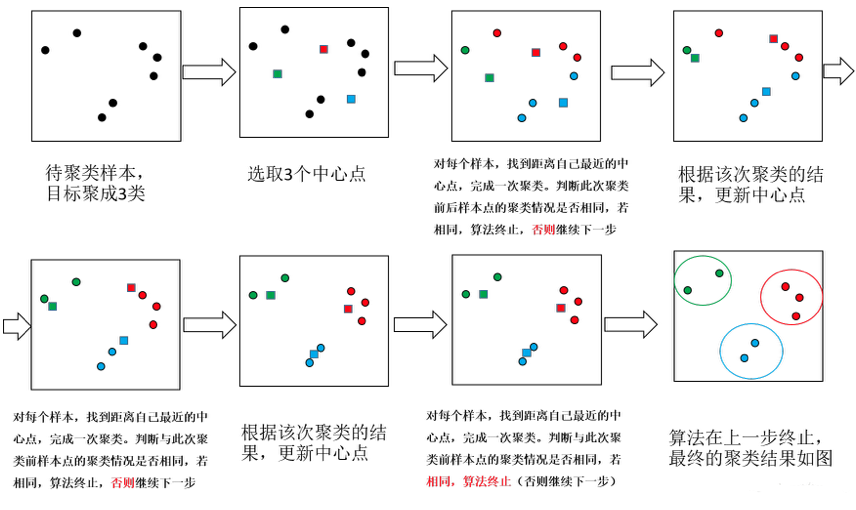
在深入探討KMeans聚類演演算法之前,瞭解其工作原理是至關重要的。本節將介紹KMeans演演算法的核心組成部分,包括資料集和特徵空間、距離度量以及演演算法的主要步驟。
資料集和特徵空間
定義:在KMeans演演算法中,資料集通常表示為一個矩陣,其中每一行是一個資料點,每一列是一個特徵。特徵空間是這些資料點存在的多維空間,通常與資料集的列數相同。
例子:假設我們有一個簡單的2D資料集,其中包括身高和體重兩個特徵。在這種情況下,特徵空間是一個二維平面,其中每個點代表一個具有身高和體重值的個體。
距離度量
定義:距離度量是一種衡量資料點之間相似度的方法。在KMeans中,最常用的距離度量是歐幾里得距離。
例子:在上面的身高和體重的例子中,我們可以使用歐幾里得距離來衡量兩個人在特徵空間中的相似度。數學上,這可以通過以下公式來表示:

演演算法步驟
KMeans演演算法主要由以下幾個步驟組成:
- 選擇K個初始中心點:隨機選擇資料集中的K個資料點作為初始中心點(質心)。
- 分配資料點到最近的中心點:對於資料集中的每一個點,計算其與所有中心點的距離,並將其分配給最近的中心點。
- 更新中心點:重新計算每個叢集的中心點,通常是該叢集內所有點的平均值。
- 迭代直至收斂:重複步驟2和步驟3,直至中心點不再顯著變化或達到預設的迭代次數。
例子:考慮一個商店希望將客戶分為幾個不同的叢集,以便進行更有效的市場推廣。商店有關於客戶年齡和購買頻率的資料。在這個例子中,KMeans演演算法可以這樣應用:
- 選擇K(例如,K=3)個客戶作為初始的中心點。
- 使用年齡和購買頻率計算所有其他客戶與這K箇中心點的距離,並將每個客戶分配給最近的中心點。
- 更新每個叢集的中心點,這裡是每個叢集內所有客戶年齡和購買頻率的平均值。
- 迭代這個過程,直至叢集不再發生變化或達到預設的迭代次數。
通過這個結構化的解析,我們能更好地理解KMeans聚類演演算法是如何工作的,以及如何在不同的應用場景中調整演演算法引數。
三、KMeans案例實戰
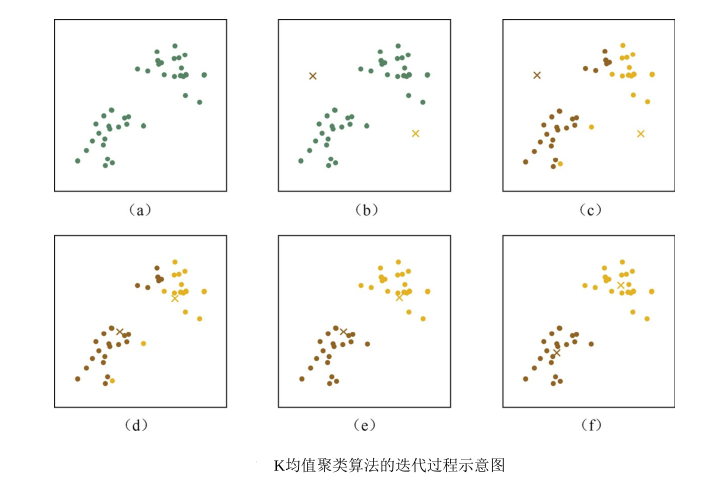
理解KMeans演演算法的理論基礎是非常重要的,但更重要的是能夠應用這些理論到實際問題中。在本節中,我們將通過一個具體的案例來演示如何使用Python和PyTorch實現KMeans演演算法。
案例背景:客戶細分
定義:客戶細分是一種市場策略,通過將潛在客戶分為不同的組或段,企業可以更精準地進行產品推廣或服務提供。
例子:一個線上零售商希望根據客戶的年齡、購買歷史和瀏覽行為來進行客戶細分,以實施更有效的行銷策略。
資料集說明
在本案例中,我們將使用一個簡單的資料集,包括客戶的年齡、購買頻率和平均消費金額三個特徵。
客戶ID | 年齡 | 購買頻率 | 平均消費金額
------|------|----------|--------------
1 | 25 | 5 | 50
2 | 30 | 3 | 40
3 | 35 | 1 | 20
...
Python實現程式碼
下面是使用Python和PyTorch來實現KMeans演演算法的程式碼。我們首先匯入必要的庫,然後進行資料準備、模型訓練和結果視覺化。
import numpy as np
import torch
import matplotlib.pyplot as plt
# 建立一個模擬資料集
data = torch.tensor([[25, 5, 50],
[30, 3, 40],
[35, 1, 20]], dtype=torch.float32)
# 初始化K箇中心點
K = 2
centers = data[torch.randperm(data.shape[0])][:K]
# KMeans演演算法主體
for i in range(10): # 迭代10次
# 步驟2:計算每個點到各個中心點的距離,並分配到最近的中心點
distances = torch.cdist(data, centers)
labels = torch.argmin(distances, dim=1)
# 步驟3:重新計算中心點
for k in range(K):
centers[k] = data[labels == k].mean(dim=0)
# 結果視覺化
plt.scatter(data[:, 0], data[:, 1], c=labels)
plt.scatter(centers[:, 0], centers[:, 1], marker='x')
plt.show()
輸出與解釋
在這個簡單的例子中,KMeans演演算法將客戶分為兩個叢集。通過視覺化結果,我們可以看到叢集中心點(標記為'x')分別位於不同的年齡和購買頻率區域。
這樣的輸出可以幫助企業更好地瞭解其客戶群體,從而制定更精準的市場策略。
四、KMeans的優缺點
理解一個演演算法的優缺點是掌握它的關鍵。在這一部分,我們將詳細討論KMeans演演算法在實際應用中的優點和缺點,並通過具體的例子來加深這些概念的理解。
優點
計算效率高
定義:KMeans演演算法具有高計算效率,尤其在資料集規模較大或特徵較多的情況下仍能保持良好的效能。
例子:假設一個大型線上零售商有數百萬的客戶資料,包括年齡、購買歷史、地理位置等多維特徵。使用KMeans,僅需幾分鐘或幾小時即可完成聚類,而更復雜的演演算法可能需要更長的時間。
演演算法簡單易於實現
定義:KMeans演演算法本身相對簡單,容易編碼和實現。
例子:如我們在前面的案例實戰部分所示,僅需幾十行Python程式碼即可實現KMeans演演算法,這對於初學者和研究人員都是非常友好的。
缺點
需要預設K值
定義:KMeans演演算法需要預先設定簇的數量(K值),但實際應用中這個數量往往是未知的。
例子:一個餐廳可能希望根據顧客的菜品選擇、消費金額和就餐時間來進行聚類,但事先很難確定應該分成幾個叢集。錯誤的K值選擇可能導致不準確或無意義的聚類結果。
對初始點敏感
定義:演演算法的輸出可能會受到初始中心點選擇的影響,這可能導致區域性最優而非全域性最優解。
例子:在處理地理資訊時,如果初始中心點不慎選在了人跡罕至的地區,可能會導致一個非常大但不具代表性的叢集。
處理非凸形狀叢集的能力差
定義:KMeans更適用於凸形狀(例如圓形、球形)的叢集,對於非凸形狀(例如環形)的叢集處理能力較差。
例子:假設一個健身房希望根據會員的年齡和鍛鍊時間進行聚類,但發現年輕人和老年人都有早晨和晚上鍛鍊的習慣,形成了一個環形的分佈。在這種情況下,KMeans可能無法準確地進行聚類。
五、KMeans在文字聚類中的應用

除了常見的數值資料聚類,KMeans也被廣泛應用於文字資料的聚類。在這一節中,我們將探討KMeans在文字聚類中的應用,特別是在自然語言處理(NLP)領域。
文字向量化
定義:文字向量化是將文字資料轉化為數值形式,以便機器學習演演算法能更容易地處理它。
例子:例如,一個常用的文字向量化方法是TF-IDF(Term Frequency-Inverse Document Frequency)。
KMeans與TF-IDF
定義:結合TF-IDF和KMeans演演算法可以有效地對檔案進行分類或主題建模。
例子:一個新聞網站可能有成千上萬的文章,它們可以通過應用KMeans聚類演演算法與TF-IDF來分類成幾大主題,如「政治」、「科技」、「體育」等。
Python實現程式碼
下面的程式碼使用Python的sklearn庫進行TF-IDF文字向量化,並應用KMeans進行文字聚類。
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.cluster import KMeans
# 模擬文字資料
documents = ["政治新聞1", "科技新聞1", "體育新聞1",
"政治新聞2", "科技新聞2", "體育新聞2"]
# TF-IDF向量化
vectorizer = TfidfVectorizer()
X = vectorizer.fit_transform(documents)
# KMeans聚類
model = KMeans(n_clusters=3)
model.fit(X)
labels = model.labels_
# 輸出與解釋
for i, label in enumerate(labels):
print(f"檔案 {documents[i]} 被歸類到 {label} 叢集。")
輸出與解釋
這個簡單的例子展示瞭如何通過KMeans與TF-IDF將文字檔案分為3個不同的叢集。對應的輸出可能如下:
檔案 政治新聞1 被歸類到 0 叢集。
檔案 科技新聞1 被歸類到 1 叢集。
檔案 體育新聞1 被歸類到 2 叢集。
檔案 政治新聞2 被歸類到 0 叢集。
檔案 科技新聞2 被歸類到 1 叢集。
檔案 體育新聞2 被歸類到 2 叢集。
通過這種方式,我們可以將大量文字資料進行分類,方便後續的資料分析或資訊檢索。
總結
KMeans聚類演演算法是一種既簡單又強大的無監督學習工具,適用於各種資料型別和應用場景。在本文中,我們深入地探討了KMeans的基本原理、實際應用、優缺點,以及在文字聚類中的特殊用途。
從計算效率和易於實現的角度來看,KMeans演演算法是一個有吸引力的選項。但它也有其侷限性,如對初始中心點的依賴性,以及在處理複雜叢集形狀時可能出現的問題。這些因素需要在實際應用中仔細權衡。
文字聚類則展示了KMeans在高維稀疏資料上也能表現出色的一面,尤其是與TF-IDF等文字向量化方法結合使用時。這為自然語言處理、資訊檢索,以至更為複雜的語意分析等應用場景鋪平了道路。
然而,值得注意的是,KMeans並不是萬能的。在不同的應用環境下,還需考慮到更為複雜的因素,比如資料分佈的不均勻性、噪聲的存在以及簇的動態性等。這些因素可能要求我們對KMeans進行適當的改進或者選擇其他更適應特定問題的聚類演演算法。
此外,未來隨著演演算法和硬體的進步,以及更多先進的優化技巧的提出,KMeans和其他聚類演演算法還將進一步演化。例如,通過自動確定最佳的K值,或者運用更先進的初始化策略,以減少對初始點選擇的依賴,都是值得進一步探究的方向。
綜上所述,KMeans是一個非常實用的演演算法,但要充分發揮其潛能,我們需要深入理解其工作原理,適應性以及侷限性,並在實際應用中做出明智的選擇和調整。希望本文能對你在使用KMeans或其他聚類演演算法時提供有價值的指導和靈感。
關注TechLead,分享AI全維度知識。作者擁有10+年網際網路服務架構、AI產品研發經驗、團隊管理經驗,同濟本復旦碩,復旦機器人智慧實驗室成員,阿里雲認證的資深架構師,專案管理專業人士,上億營收AI產品研發負責人。
如有幫助,請多關注
TeahLead KrisChang,10+年的網際網路和人工智慧從業經驗,10年+技術和業務團隊管理經驗,同濟軟體工程本科,復旦工程管理碩士,阿里雲認證雲服務資深架構師,上億營收AI產品業務負責人。