技術文章 » 論文精讀：用於少樣本目標檢測的元調整損失函數和資料增強（Meta-tuning Loss Functions and Data Augmentation for Few-shot Object Det

論文精讀：用於少樣本目標檢測的元調整損失函數和資料增強（Meta-tuning Loss Functions and Data Augmentation for Few-shot Object Det

2023-11-15 21:00:47

論文連結：Meta-Tuning Loss Functions and Data Augmentation for Few-Shot Object Detection

Abstract

現階段的少樣本學習技術可以分為兩類：基於微調（fine-tuning）方法和基於元學習（meta-learning）方法。

基於元學習的方法旨在學習專用的元模型，使用學到的先驗知識處理新的類，而基於微調的方法以更簡單的方式處理少樣本檢測，通過基於梯度的優化將檢測模型適應新領域的目標。基於微調的方法相對簡單，但通常能夠獲得更好的檢測結果。

基於此，作者將重點關注損失函數和資料增強對微調的影響，並使用元學習的思想去動態調整引數。因此，提出的訓練方案允許學習能促進少樣本檢測的歸納偏置，從而增強少樣本檢測，同時保持微調方法的優點。

歸納偏置：為了實現泛化，一定的偏好（或者稱為歸納偏置）是必要的，也就說在新資料集上實現泛化需要對最優解做出合理假設。引入歸納偏置的方式有很多，例如在目標函數中加入正則項。

1. Introduction

目標檢測是計算機視覺的問題之一，依賴於大規模註釋資料集，但由於資料集的收集和標註成本，催生出了一系列對標註資料要求較低的目標檢測方法，例如結合弱監督學習、點註釋（point annotations）和混合監督學習。類似的還有少樣本目標檢測（Few-Shot Object Detection, FSOD）。

在FSOD問題上，目標是通過遷移學習，用在大規模影象上訓練的模型，為具有少量樣本標記的新類構建檢測模型。還有就是廣義少樣本目標檢測（Generalized-FSOD, G-FSOD），目標是要構建在基礎類和新類都表現良好的少樣本檢測模型。

FSOD分為元學習的方法與微調的方法。現階段，微調的方法在這一問題上表現更為出色。微調的方法是典型的遷移學習，基於梯度優化進行對正則化損失最小化，使預訓練模型適應少樣本類別。

雖然能夠對專門的引數進行訓練的FSOD的元學習方法很有吸引力，但有兩個重要的缺點：1、由於模型複雜性，有著過擬合訓練類的風險；2、難以解釋學到的內容。相對的，基於微調的FSOD方法簡單且通用。

為什麼說「難以解釋學到的內容」：除了廣為詬病的「神經網路模型是黑盒子」說法，還可能是因為元學習涉及多個任務的訓練，任務之間亦有差異，這使得難以找到的通用的解釋方法。

但是，基於微調的FSOD方法的最大優點也可能是最大缺點：它們普遍保留基礎類別的知識，沒有在很少的樣本上學習到歸納偏置。為了解決這些問題，許多方法在微調的細節切入，例如：Frustratingly Simple Few-Shot Object Detection提出凍結一部分引數然後微調檢測模型的最後一層；FSCE: Few-Shot Object Detection via Contrastive Proposal Encoding修改了損失函數。然而這些這些針對少樣本類的特定優化方式，由於都是手工完成，所以並不一定是最優的。

還是為了解決這些問題，作者引入元學習的思想，在FSOD的微調階段調整損失函數和資料增強，這個過程稱為元微調（meta-tuning），如圖1所示。

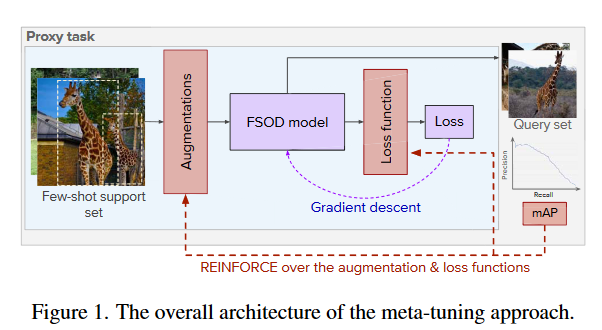
具體來說，就像元學習訓練元模型一樣，以資料驅動的方式逐步發現適合FSOD的最佳損失函數和資料（細節）增強。使用強化學習（Reinforcement Learning, RL）的技術調整損失函數與資料增強，最大化微調後的FSOD模型質量。作者通過對設定的損失項和增強列表進行調整，將搜尋限制在有效的函數族內。最後將元學習調整的損失函數和增強以及FSOD特定的歸納偏置與微調方法相結合。

為了探索meta-tuning對於FSOD的潛力，作者將重點關注分類損失的細節（FSCE: Few-Shot Object Detection via Contrastive Proposal Encoding展示了，在目標檢測問題中，分類和定位中，分類更容易出錯）。此外，作者首先關注了softmax的溫度引數，設定了兩個版本：1、簡單的恆定溫度引數；2、隨微調迭代變化的動態溫度，用指數多項式表示。

在所有情況下，通過meta-tuning學習的引數都會產生可解釋的損失函數，與複雜的元模型相比，在基礎類別上過擬合的風險可以忽略不計。作者還在meta-tuning過程中對資料增強的進行建模，作者還引入了分數縮放器，用於平衡學習基礎類別和新類的分數。

2. Related Word（略）

3. Method

每張訓練圖片對應元組\((x,y)\)，包括影象\(x\)和標註\(y=\{y_0,\dots,y_M\}\)，每個物件的標註\(y_i=\{c_i,b_i\}\)表示類別標籤\(c_i\)和檢測邊界\(b_i=\{x_i,y_i,w_i,h_i\}\)。當FSOD模型訓練完成，評估階段使用k張圖片，影象的類來自新的類集合\(C_n\)。

對於基礎模型，作者使用MPSR FSOD方法 作為損失函數和資料增強搜尋方法的基礎。為了使Faster-RCNN適應基於微調的FSOD，引入了多尺度位置取樣調整（Multi-Scale Positive Sample Refinement, MPSR）分支來處理尺度稀疏問題

影象中的物件被裁剪並調整為多種尺寸以建立物件金字塔。MPSR對區域提議網路（Region Prosed Network, RPN）和檢測頭使用兩組損失函數，並將不同比例的正樣本與主檢測分支檢測結果一起反饋到損失函數中。最後，作者認為所提出的方法原則上可以應用於幾乎任何基於微調的 FSOD 模型。

3.1 Meta-Tuning損失函數

對於元調整的FSOD，將重點關注分類損失函數（正如上文所述，分類比檢測更容易出錯）。對於MPSR的損失函數表示為：

\[\mathcal{l}_{cls}(x,y)=-\frac{1}{N_{ROI}}\sum^{N_{ROI}}_i\log(\frac{e^{f(x_i,y_i)}}{\sum_y=e^{f(x_i,y)}}) \tag{1} \]

其中\(N_{ROI}\)是影象的候選區域，\(y_i\)是第i個ROI的真實標籤，\(f(x_i,y)\)是對應y的預測分數。為了使損失函數更靈活，重新定了損失函數：\(\mathcal{l}_{cls}(x,y;\rho)\)，其中\(\rho\)表示損失函數的引數。首先引入了溫度標量\(\rho_\tau\)，即\(\rho=(\rho_\tau)\)。

\[\mathcal{l}_{cls}(x,y;\rho)=-\frac{1}{N_{ROI}}\sum^{N_{ROI}}_i\log(\frac{e^{f(x_i,y_i)/\rho_\tau}}{\sum_{y'}=e^{f(x_i,y')/\rho_\tau}}) \tag{2} \]

引入的動機是來自溫度縮放在其他問題的表現，例如知識蒸餾。對比手動調整的方式，這裡引入元調整，通過定義動態溫度函數\(f_p\)和新類縮放器\(\alpha\)使損失函數更復雜：

\[\mathcal{l}_{cls}(x,y;\rho)=-\frac{1}{N_{ROI}}\sum^{N_{ROI}}_i\log(\frac{\alpha(y_i)e^{f(x_i,y_i)/f_p(t)}}{\sum_{y'}=e^{\alpha(y')f(x_i,y')/f_p(t)}}) \tag{3} \]

其中\(f_p(t)=\exp(\rho_at^2+\rho_bt+\rho_c)\)，這裡\(\rho=(\rho_a,\rho_b,\rho_c)\)是多項式係數三元組，\(t\in[0,1]\)為歸一化後的微調迭代索引。\(y\in C_b\)時，\(\alpha(y)=1\)；否則用縮放係數\(\rho_\alpha\)平衡基礎類別和新類的學習。

3.2 Meta-tuning增強

對於元調整的資料增強部分，考慮到在基礎類別學習的結果要遷移到新類，作者專注於光度增強。作者使用共用的增強幅度引數\(\rho_{aug}\)對亮度、飽和度和色調進行建模。在Randaugment: Practical Automated Data Augmentation With a Reduced Search Space證明了這是有效的。

3.3 Meta-tuning過程

作者使用基於強化學習的REINFORCE去搜尋最佳損失函數和增強。

為了提高泛化能力，設定了代理任務：在基礎類別訓練資料上，模範新類的FSOD任務。為此，基礎類別被分為兩個子集，代理基礎類別\(C_{p-base}\)和代理新類\(C_{p-novel}\)。同時，使用基礎類別訓練集分割構造3個不重疊的資料集：

  1. \(D_{p-pretrain}\)，僅包含\(C_{p-base}\)的樣本，用來訓練臨時的目標檢測模型進行元調整；
  2. \(D_{p-support}\)，包含\(C_{p-base}\cup C_{p-novel}\)，在元調整期間充當微調資料；
  3. \(D_{p-query}\)，包含\(C_{p-base}\cup C_{p-novel}\)，在元調整期間評估廣義FSOD效能。

就像元學習的task，本文設定了一系列FSOD代理任務：在每個代理任務T，從\(D_{p-support}\)選擇訓練資料。此外，還有對損失函數/增強幅度的引數組合\(\rho\)，這裡每個\(\rho_j\in\rho\)服從高斯分佈：\(\rho_j\sim\mathcal{N}(\mu_j,\sigma^2)\)。

使用取樣的\(\rho\)對應的損失函數或資料增強，在支援影象上基於梯度優化微調初始模型，並在\(D_{p-query}\)計算平均精度（mean Average Precision, mAP）。通過在多個代理任務支援樣本上多次重複該過程獲得多個mAP分數，然後在每一次訓練之後，通過REFORCE規則更新\(\mu\)進行元調整，以找到表現良好的\(\rho\)。

\[\mu'_j\leftarrow\mu_j+\eta R(\rho)\nabla_\mu\log(p(\rho_j;\mu_j,\sigma))\tag{4} \]

其中\(p(\rho;\mu,\sigma)\)是高斯密度函數，\(\eta\)是RL學習率。

我們以每次訓練得到獎勵最高的\(\rho\)作為REFORCE更新規則。\(R(\rho)\)是通過白化後的mAP分數獲得的歸一化獎勵函數.

白化：白化的目的是使得預處理後的資料具有以下特性：1、特徵之間的相關性儘可能小；2、所有特徵具有相同的方差；3、所有特徵具有相同的均值。

最後，從\(\sigma=0.1\)開始，在RL迭代中減小\(\sigma\)，通過更保守的取樣逐步減小探索，從而提高收斂性，最終方案如圖2所示（作者真正的工作是「ROI Cls Loss」和下方根據AP更新\(\mu\)的部分，Refinement Branch與Object Detection來自MPSR）：

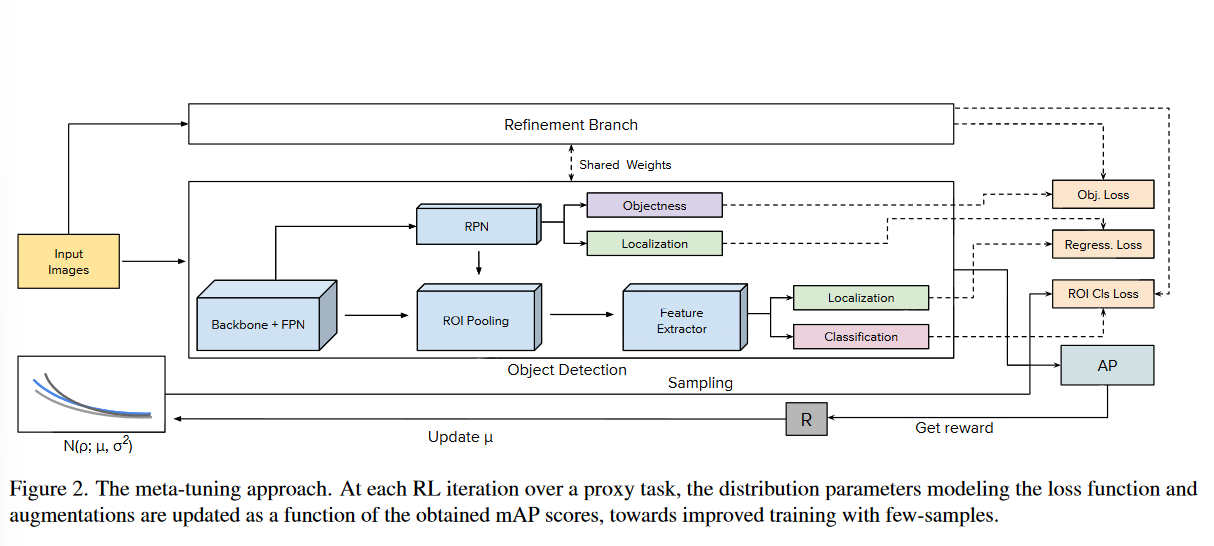
4. Experiments

對於指標的設定，作者選擇mAP分別評估基礎類和新類的檢測結果。在廣義FSOD評估中，選擇調和平均值（Harmony Mean, HM）來計算效能，HM定義為\(\mathrm{mAP_{base}}\)和\(\mathrm{mAP_{novel}}\)的均值。

對於資料集。在Pascal VOC上存在3個獨立的基礎類別/新類，其中每個由15個基礎類別和5個新類組成。在每次分割，選擇5個基礎類別模仿代理任務上的新類。在MS-COCO上，選擇15個基礎類別模仿代理任務上的新類，並評估10-shot和30-shot的情況。

對於Baseline，作者使用了MPSR和DeFRCN，兩種FSOD上的SOTA演演算法

4.1 主要結果

作者首先將元調整結果與MPSR基線進行比較,如表1所示。

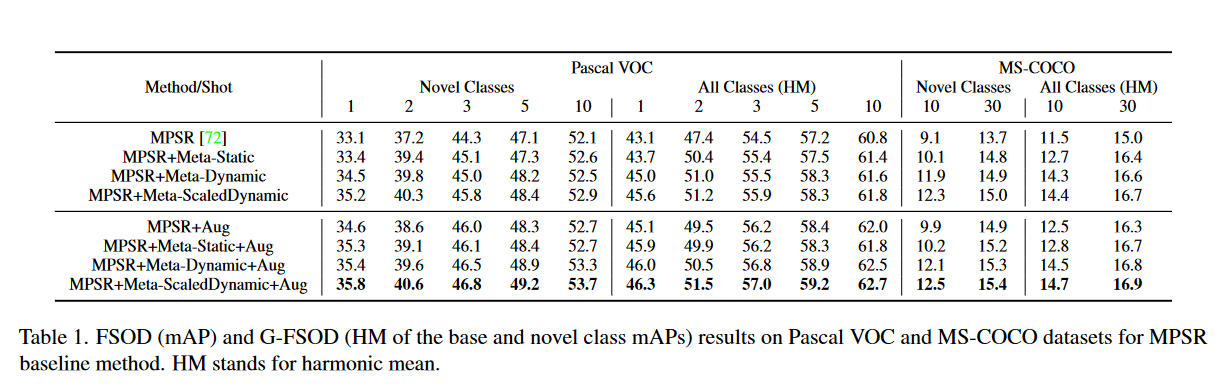
  • Meta-Static：使用固定的溫度引數；
  • Meta-Dynamic：使用動態溫度引數（公式（3）無\(\alpha\)）；
  • Meta-ScaledDynamic：使用新類縮放動態溫度函數（公式（3））；
  • Aug：表示資料增強。

可以看到，隨著演演算法改進和資料增強引數的新增，整體的表現得到了提高。

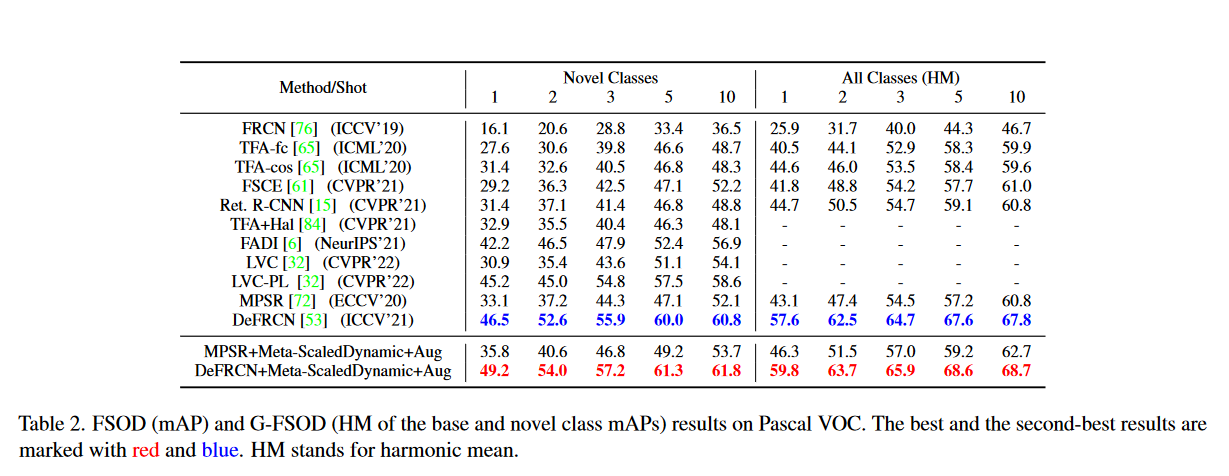
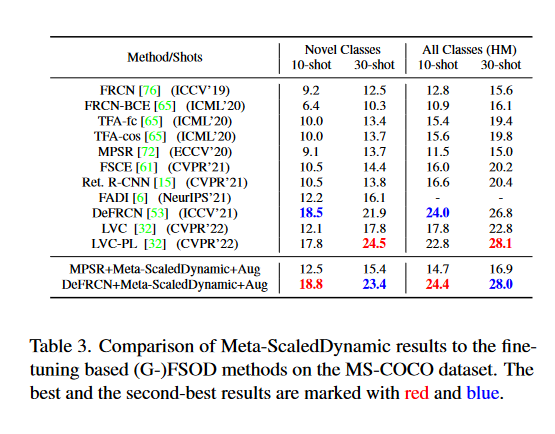
表2中展示不同演演算法在Pascal VOC上的對比，可以看到作者的方法在FSOD和G-FSOD上都取得了最高的得分。結果表明，將元學習的得到的歸納偏置與微調相結合是有效的。

圖3第一行、第二行分別展示了沒有元調整和有元調整（帶縮放動態溫度和資料增強）的視覺檢測範例。可以看到誤報減少、框更準確。
表3中展示了在MS-COCO上的對比，除了遜色於DeFRCN和LVC-PL，較其他演演算法都有改進。

4.2 消融研究

消融研究設計了元微調的三個細節：

  1. 代理任務的模仿：在代理任務上進行強化學習，用來模仿測試時的FSOD。
  2. 模型重新初始化：在每個代理任務上重新初始化模型，以避免累積的模型更新對獎勵的不良影響。
  3. 獎勵歸一化：通過標準化單個任務中獲得的獎勵來進一步減少任務間方差的影響，從而允許對取樣的損失函數和增強進行更獨立的評估。

在表4中展示使用Pascal VOC Split-1 和 MPSR+Meta-Dynamic和5-shot在G-FSOD上的表現。

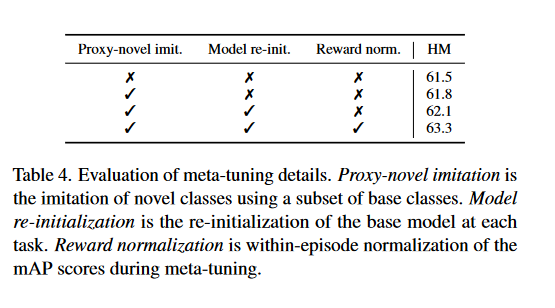
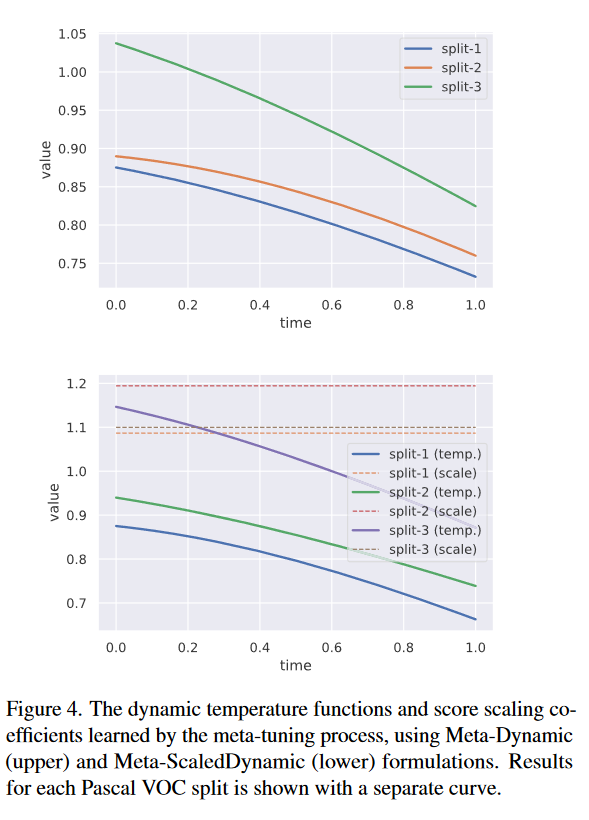
圖4中展示了公式（2）和公式（3）使用的損失函數的相關引數訓練變化。

5. Conclusion

基於微調的少樣本目標檢測模型簡單可靠。但現有的微調改進都是使用手工的方式，作者提出引入元學習和強化學習，為小樣本學習引入歸納偏置，使損失函數和資料增強幅度的學習變化可解釋。最後，提出的元調整方式在資料集上取得較好的效能提升。

參考文獻