多樣本向量化

• 與上篇部落格相聯絡的來理解

邏輯迴歸是將各個訓練樣本組合成矩陣，對矩陣的各列進行計算。神經網路是通過對邏輯迴歸中的等式簡單的變形，讓神經網路計算出輸出值。這種計算是所有的訓練樣本同時進行的，以下是實現它具體的步驟：

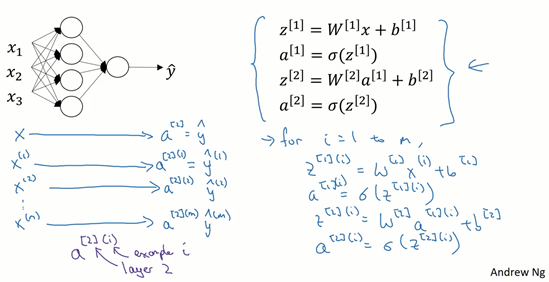
圖1.4.1

上篇部落格中得到的四個等式。它們給出如何計算出\(z^{[1]}\)，\(a^{[1]}\)，\(z^{[2]}\)，\(a^{[2]}\)。

對於一個給定的輸入特徵向量\(X\)，這四個等式可以計算出\(\alpha^{[2]}\)等於\(\hat{y}\)。這是針對於單一的訓練樣本。如果有\(m\)個訓練樣本,那麼就需要重複這個過程。

用第一個訓練樣本\(x^{[1]}\)來計算出預測值\(\hat{y}^{[1]}\)，就是第一個訓練樣本上得出的結果。

然後，用\(x^{[2]}\)來計算出預測值\(\hat{y}^{[2]}\)，迴圈往復，直至用\(x^{[m]}\)計算出\(\hat{y}^{[m]}\)。

用啟用函數表示法，如上圖左下所示，它寫成\(a^{[2](1)}\)、\(a^{[2](2)}\)和\(a^{[2](m)}\)。

【注】：\(a^{[2](i)}\)，\((i)\)是指第\(i\)個訓練樣本而\([2]\)是指第二層。

如果有一個非向量化形式的實現，而且要計算出它的預測值，對於所有訓練樣本，需要讓\(i\)從1到\(m\)實現這四個等式：

\(z^{[1](i)}=W^{[1](i)}x^{(i)}+b^{[1](i)}\)

\(a^{[1](i)}=\sigma(z^{[1](i)})\)

\(z^{[2](i)}=W^{[2](i)}a^{[1](i)}+b^{[2](i)}\)

\(a^{[2](i)}=\sigma(z^{[2](i)})\)

對於上面的這個方程中的\(^{(i)}\)，是所有依賴於訓練樣本的變數，即將\((i)\)新增到\(x\)，\(z\)和\(a\)。如果想計算\(m\)個訓練樣本上的所有輸出，就應該向量化整個計算，以簡化這列。

這裡需要使用很多線性代數的內容，重要的是能夠正確地實現這一點，尤其是在深度學習的錯誤中。實際上我認真地選擇了運運算元號，這些符號只是針對於我所寫神經網路系列的部落格的，並且能使這些向量化容易一些。

所以，希望通過這個細節可以更快地正確實現這些演演算法。接下來講講如何向量化這些：
公式1.12：

公式1.13：

公式1.14：

公式1.15：

定義矩陣\(X\)等於訓練樣本，將它們組合成矩陣的各列，形成一個\(n\)維或\(n\)乘以\(m\)維矩陣。接下來計算見公式1.15：

以此類推，從小寫的向量\(x\)到這個大寫的矩陣\(X\)，只是通過組合\(x\)向量在矩陣的各列中。

同理，\(z^{[1](1)}\)，\(z^{[1](2)}\)等等都是\(z^{[1](m)}\)的列向量，將所有\(m\)都組合在各列中，就的到矩陣\(Z^{[1]}\)。

同理，\(a^{[1](1)}\)，\(a^{[1](2)}\)，……，\(a^{[1](m)}\)將其組合在矩陣各列中，如同從向量\(x\)到矩陣\(X\)，以及從向量\(z\)到矩陣\(Z\)一樣，就能得到矩陣\(A^{[1]}\)。

同樣的，對於\(Z^{[2]}\)和\(A^{[2]}\)，也是這樣得到。

這種符號其中一個作用就是，可以通過訓練樣本來進行索引。這就是水平索引對應於不同的訓練樣本的原因，這些訓練樣本是從左到右掃描訓練集而得到的。

在垂直方向，這個垂直索引對應於神經網路中的不同節點。例如，這個節點，該值位於矩陣的最左上角對應於啟用單元，它是位於第一個訓練樣本上的第一個隱藏單元。它的下一個值對應於第二個隱藏單元的啟用值。它是位於第一個訓練樣本上的，以及第一個訓練範例中第三個隱藏單元，等等。

當垂直掃描，是索引到隱藏單位的數位。當水平掃描，將從第一個訓練範例中從第一個隱藏的單元到第二個訓練樣本，第三個訓練樣本……直到節點對應於第一個隱藏單元的啟用值，且這個隱藏單元是位於這\(m\)個訓練樣本中的最終訓練樣本。

從水平上看，矩陣\(A\)代表了各個訓練樣本。從豎直上看，矩陣\(A\)的不同的索引對應於不同的隱藏單元。

對於矩陣\(Z，X\)情況也類似，水平方向上，對應於不同的訓練樣本；豎直方向上，對應不同的輸入特徵，而這就是神經網路輸入層中各個節點。

神經網路上通過在多樣本情況下的向量化來使用這些等式。