OpenGL 攝像機視角詳解
1. 攝像機
攝像機就好像是我們的眼睛,我們從攝像機的方向觀察世界空間中的模型。攝像機遠離模型,模型自然就變小了(透視投影下),然而,在GL中事實上並沒有攝像機的概念。但是我們可以通過移動世界空間遠離我們的攝像機來模擬攝像機遠離世界的感覺。這也正是在上一章中,我們的觀察矩陣是(0,0,-3)的原因。我們通過將世界矩陣向螢幕裡移動3個單位模擬攝像機向螢幕外移動三個單位。
上一章中,我們只是很簡單的設定了一個觀察矩陣,這一章,我們來仔細說一下如何設定這個觀察矩陣,也就是,如何確定攝像機所在的座標系。
2. 視察矩陣
事實上我們所要做的事就是確定一個觀察矩陣,就可以完成從世界空間到觀察空間的轉換。而這在三維空間內,實際就是確定觀察空間座標系相對於世界空間座標系的位置及各軸的夾角即可。如果你空間感足夠好的話,或者相對位置足夠簡單的話,你可能很快的就可以寫出觀察座標系的表示式。但情況比較複雜的時候你可能需要耗費大量時間去完成這個轉換,下面,我將嘗試用一個通俗易懂的方式來介紹一下如何去生成這個座標。
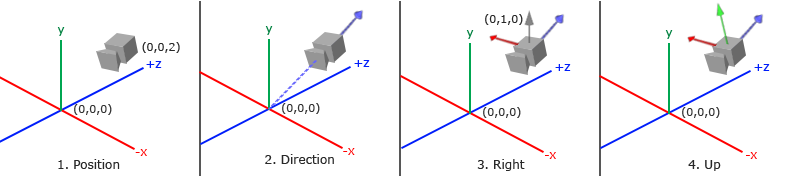
3. 攝像機的位置
這個很好理解,比如你規定了地面上一個物體作為世界的原點,那麼隨著你眼睛相對遠點的位置改變時,你所看到的物體的樣子也會隨之改變。所以眼睛相對於遠點的位置會直接影響物體的樣子,同理,我們也需要確定攝像機相對於世界空間座標原點的位置。這裡你可以看下上面圖中的第一個圖片來理解。座標系就是世界空間,我們要確定的就是攝像機在世界空間中的位置。
4. 攝像機的方向
同樣,即是你站在一個位置不動,你將目光集中在物體上不同的點時,你所看到的物體也不同。或者說,你目光的方向改變時,物體也跟著改變。同理,我們還需要確定攝像機觀察的方向。第二張圖中就顯示了攝像機在當前位置看向世界空間遠點的範例。
5. 攝像機的滾轉角
好了,現在你站在一個位置不動,目光也一直盯著物體的中心點不動,你還可以讓你看到的物體改變。除了閉眼睛,你還可以歪一下頭,你看到的東西是不是斜過來了(你非說沒變那是因為強大的大腦已經幫你轉換回來了又,你可以把眼睛換成手機攝像頭然後傾斜手機再看看,手動滑稽)。所以,我們要確定攝像機在世界空間中擺放的夾角。這麼表述可能不清楚,稍微借一點座標系的概念。我們攝像機的方向就是觀察座標系的Z軸。但是一個Z軸確定卻並不能確定一個座標系,我們至少要確定兩個座標軸,才能通過兩個座標軸確定第三個座標軸從而建立一個座標系。第四張圖就顯示了確定三個軸夾角後的座標系。
6. 視察座標系
經過上面的論述,我們知道了,我們只要知道攝像機的位置、攝像機的方向和x或y軸中任意一個軸的方向即可確定。
如果我們不改變滾轉角保證了攝像機座標系的x軸與世界座標系的y軸總是空間垂直,我們就可以通過攝像機方向向量與世界座標系的y軸的方向向量叉乘從而獲得攝像機座標系的x軸(兩向量叉乘將獲得同時垂直於兩個向量的第三個向量)。
Look At
我們已經知道如何去構建一個攝像機座標系了,不過怎麼通過這些元素構建出觀察矩陣呢?glm為我們提供了LookAt(position,target,up)函數。它含有三個引數:
- position,第一個引數就是我們攝像機在世界座標系的位置了
- target,第二個引數是我們觀察的點的位置,就是我們目光匯聚的那個點了,為什麼是目標點呢?因為通過position減去target我們就可以獲得攝像機方向的向量了
- up,第三個引數是一個與攝像機座標系x軸垂直的向量。為什麼是這個向量呢?因為我們可以通過position和target確定攝像機的方向,也就是攝像機座標系z軸。再找到一個也與x軸垂直的向量即可確定x軸的方向向量了。
所以,上一章中我們生成的觀察矩陣可以通過lookAt函數這樣生成:

上面函數中,描述了我們的攝像機在世界座標系的(0,0,3)位置,我們觀察的點就是世界座標原點,這個up向量就是世界座標系的y軸的方向向量。
7. 圓周運動
那麼現在,我們將我們的target保持在(0,0,0)這個點上,通過改變position來改變我們的lookAt矩陣。我們可以大概猜想一下結果就應該是我們圍著一個東西轉圈一直盯著這個東西的樣子。
下面這段程式碼在渲染迴圈中:

8. 水平運動
接下來我們來模擬一下我們日常生活中的視角。我們想一下,一定是我們相對世界的position一直是改變的,我們眼睛的焦距是不變的,始終看我們自身位置前的某一個位置。
那麼lookAt函數變成了這樣:

那麼現在我們還是隻要改變我們的position就好了。
這裡我們用鍵盤來接收我們想要做的移動的輸入,程式碼如下:

上述左右移動時,我們看到我們用front向量與up向量相乘後標準化獲取了right向量。這裡之所以直接使用世界座標系中的front向量和up向量,是因為我們當前觀察角度的攝像機座標系與世界座標是的各軸完全是平行的,只是原點不同而已。
這樣,我們就在這個世界中可以前後左右自由移動了。
9. 移動速度
我們看到,我們處理鍵盤輸入是在渲染迴圈中處理的。試想如果我們的渲染迴圈迴圈一次的事件長,那麼我們改變position經過的時間間隔就長,反之就短。那麼如果一次渲染迴圈的時間是在一個範圍內浮動的,那麼物體運動的速度看起來也就是一個浮動的過程,我們應該監測每次渲染迴圈(更準確的應該是每次鍵盤事件處理)的時間間隔,通過這個時間間隔決定我們這一次position改變的數量。
這裡我們只要將我們之前定義的攝像機的速度在乘上一個時間間隔係數即可:

10. 視角移動
目前為止,我們實現了在世界中水平自由移動了,但是我們還不能轉頭也不能擡頭。我們只要改變我們觀察點的位置即可。這裡,為了保證我們的焦距是不變的,所以我們要將front向量標準化。
現在我們的攝像機座標系與世界座標系的各軸是平行的。我們想擡頭呢,我們就以x軸旋轉座標系,想左右牛頭就以y軸旋轉座標系即可。
11. 尤拉角
我們先來看一下座標系旋轉角的概念和圖示。
尤拉角(Euler Angle)是可以表示3D空間中任何旋轉的3個值,由萊昂哈德·尤拉(Leonhard Euler)在18世紀提出。一共有3種尤拉角:俯仰角(Pitch)、偏航角(Yaw)和滾轉角(Roll)。
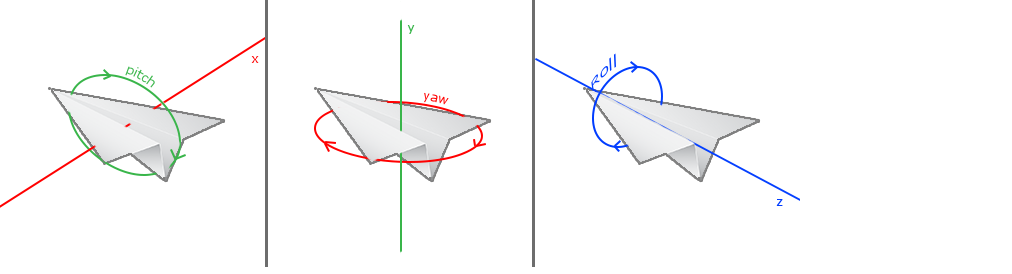
俯仰角是描述我們如何往上或往下看的角,可以在第一張圖中看到。第二張圖展示了偏航角,偏航角表示我們往左和往右看的程度。滾轉角代表我們如何翻滾攝像機,通常在太空飛船的攝像機中使用。每個尤拉角都有一個值來表示,把三個角結合起來我們就能夠計算3D空間中任何的旋轉向量了。
我們來看一下如何計算這個向量。


12. 滑鼠輸入
首先,我們要告訴GL,如果捕捉遊標的話,我們不應該展示遊標(當然你也可以展示)。
glfwSetInputMode(window, GLFW_CURSOR, GLFW_CURSOR_DISABLED);然後我們應該設定滑鼠事件的回撥:
glfwSetCursorPosCallback(window, mouse_callback);接下來就是回撥函數了:

13. 縮放
目前為止,我們可以自由在世界中移動,改變視角了已經。但是我們還想給攝像機新增一個縮放功能,你可能說我走近點東西不就大了麼。的確是這樣的,不過我們也可以在原地做到這件事。我們可以利用透視的特性完成這件事。在同樣的距離觀察一個物體,視野越小時,我們能觀察到的物體的部分越小,但是我們的螢幕是不變的,也就是螢幕上顯示的物體的部分越小,這樣就好像物體被放大了一樣。所以我們只要改動這個fov值就可以完成縮放。