一文搞懂雙連結串列
前言
前面有很詳細的講過線性表(順序表和連結串列),當時講的連結串列以單連結串列為主,但在實際應用中雙連結串列有很多應用場景,例如大家熟知的LinkedList。

雙連結串列與單連結串列區別
單連結串列和雙連結串列都是線性表的鏈式實現,它們的主要區別在於節點結構。單連結串列的節點包含資料欄位 data 和一個指向下一個節點的指標 next,而雙連結串列的節點除了 data 和 next,還包含指向前一個節點的指標 pre。這個區別會導致它們在操作上有些差異。
單連結串列:
單連結串列的一個節點,有儲存資料的data,還有後驅節點next(指標)。單連結串列想要遍歷的操作都得從前節點—>後節點。

雙連結串列:
雙連結串列的一個節點,有儲存資料的data,也有後驅節點next(指標),這和單連結串列是一樣的,但它還有一個前驅節點pre(指標)。

雙連結串列結構的設計
上一篇講單連結串列的時候,當時設計一個帶頭結點的連結串列就錯過了不帶頭結點操作方式,這裡雙連結串列就不帶頭結點設計實現。所以本文構造的這個雙連結串列是:不帶頭節點、帶尾指標(tail)的雙向連結串列。
對於連結串列主體:
public class DoubleLinkedList<T> {
private Node<T> head;
private Node<T> tail;
private int size;
public DoubleLinkedList(){
this.head = null;
this.tail = null;
size = 0;
}
public void addHead(T data){}
public void add(T data, int index){}
public void addTail(T data){}
public void deleteHead(){}
public void delete(int index){}
public void deleteTail(int index){}
public T get(int index){}
public int getSize() {
return size;
}
private static class Node<T> {
T data;
Node<T> pre;
Node<T> next;
public Node() {
}
public Node(T data) {
this.data = data;
}
}
}
具體操作分析
對於一個連結串列主要的操作還是增刪,查詢的話不做詳細解釋。
剖析增刪其實可以發現大概有頭插入、編號插入、末尾插入、頭刪除、編號刪除、尾刪除幾種情況。然而這幾種關於頭尾操作的可能會遇到臨界點比如連結串列為空時插入刪除、或者刪除節點連結串列為空。
這個操作是不帶頭結點的操作,所以複雜性會高一些!
頭插入
頭插入區分頭為空和頭不為空兩種情況
頭為空:這種情況head和tail都指向新節點
頭不為空:
- 新節點的next指向head
- head的pre指向新節點
- head指向新節點(認新節點為head)

尾插入
尾插需要考慮tail為null和不為null的情況。流程和頭插類似,需要考慮tail指標最後的指向。
tail為null:此時head也為null,head和tail指向新節點。
tail不為null:
- 新節點的pre指向tail
- tail的next指向新節點
- tail指向新節點
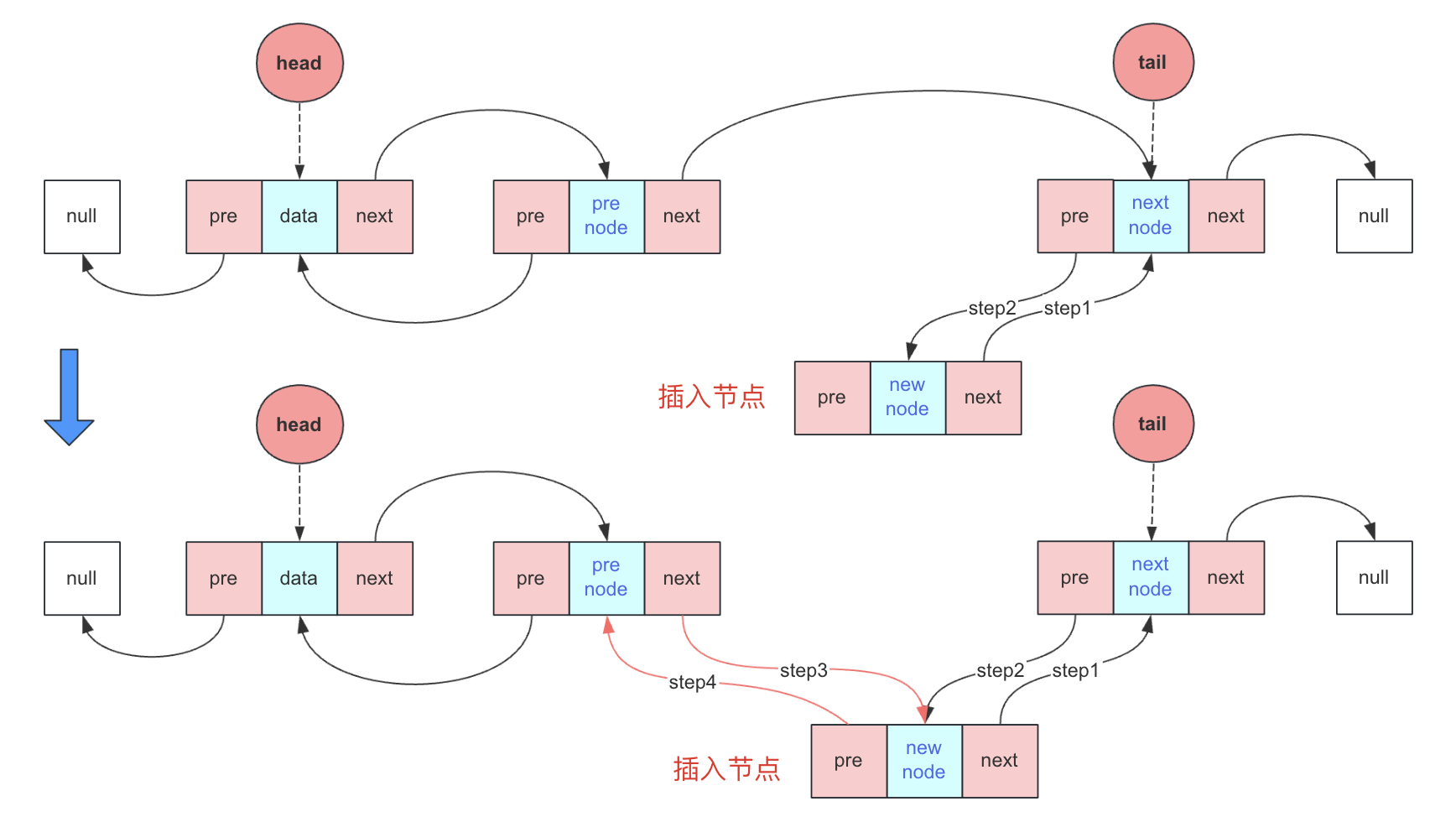
編號插入
按編號插入分情況討論,如果是頭插或者尾插就直接呼叫對應的方法。普通方法的實現方式比較靈活,可以找到前驅節點和後驅節點,然後進行指標插入,但是往往很多時候只用一個節點完成表示和相關操作,就非常考驗對錶示的理解,這裡假設只找到preNode節點。
index為0:呼叫頭插
index為size:呼叫尾插
index在(0,size):
- 找到前驅節點preNode
- 新節點next指向nextNode(此時用preNode.next表示)
- nextNode(此時新節點.next和preNode.next都可表示)的pre指向新節點
- preNode的next指向新節點
- 新節點的pre指向preNode
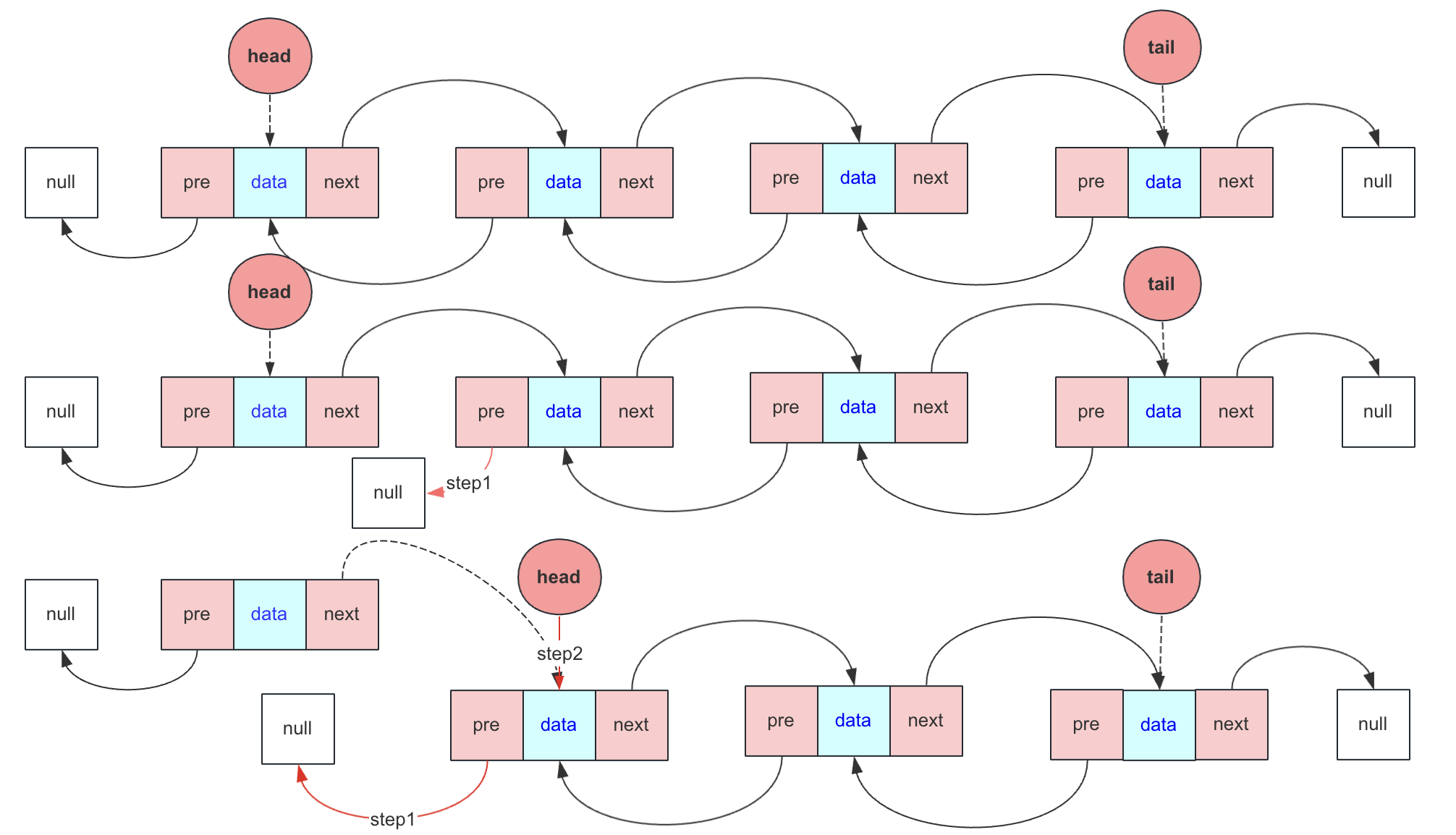
頭刪除
頭刪除需要注意的就是刪除不為空時候頭刪除只和head節點有關
head不為null:
- head = head.next 表示頭指標指向下一個節點
- head 如果不為null(有可能就一個節點),head.pre = null 斷掉與前一個節點聯絡 ;head如果為null,說明之前就一個節點head和pre都指向第一個節點,此時需要設定tail為null。
尾刪除
尾刪除和頭刪除類似,考慮好tail節點情況
如果tail不為null:
- tail = tail.pre
- 如果tail不為null,那麼tail.next = null 表示刪除最後一個,如果tail為null,說明之前head和tail都指向一個唯一節點,這時候需要head = null。
編號刪除
編號刪除和編號插入類似,先考慮是否為頭尾操作,然後再進行正常操作。
index為0:呼叫頭刪
index為size:呼叫尾刪
index在(0,size):
- 找到待刪除節點current
- 前驅節點(current.pre)的next指向後驅節點(current.next)
- 後驅節點的pre指向前驅節點

完整程式碼
根據上面的流程,實現一個不帶頭結點的雙連結串列,在查詢方面,可以根據靠頭近還是尾近,選擇從頭或者尾開始遍歷。
程式碼:
/*
* 不帶頭節點的
*/
package code.linearStructure;
/**
* @date 2023.11.02
* @author bigsai
* @param <T>
*/
public class DoubleLinkedList<T> {
private Node<T> head;
private Node<T> tail;
private int size;
public DoubleLinkedList() {
this.head = null;
this.tail = null;
size = 0;
}
// 在連結串列頭部新增元素
public void addHead(T data) {
Node<T> newNode = new Node<>(data);
if (head == null) {
head = newNode;
tail = newNode;
} else {
newNode.next = head;
head.pre = newNode;
head = newNode;
}
size++;
}
// 在指定位置插入元素
public void add(T data, int index) {
if (index < 0 || index > size) {
throw new IndexOutOfBoundsException("Index is out of bounds");
}
if (index == 0) {
addHead(data);
} else if (index == size) {
addTail(data);
} else {
Node<T> newNode = new Node<>(data);
Node<T> preNode = getNode(index-1);
//step 1 2 新節點與後驅節點建立聯絡
newNode.next = preNode;
preNode.next.pre = newNode;
//step 3 4 新節點與前驅節點建立聯絡
preNode.next = newNode;
newNode.pre = preNode;
size++;
}
}
// 在連結串列尾部新增元素
public void addTail(T data) {
Node<T> newNode = new Node<>(data);
if (tail == null) {
head = newNode;
tail = newNode;
} else {
newNode.pre = tail;
tail.next = newNode;
tail = newNode;
}
size++;
}
// 刪除頭部元素
public void deleteHead() {
if (head != null) {
head = head.next;
if (head != null) {
head.pre = null;
} else { //此時說明之前head和tail都指向唯一節點,連結串列刪除之後head和tail都應該指向null
tail = null;
}
size--;
}
}
// 刪除指定位置的元素
public void delete(int index) {
if (index < 0 || index >= size) {
throw new IndexOutOfBoundsException("Index is out of bounds");
}
if (index == 0) {
deleteHead();
} else if (index == size - 1) {
deleteTail();
} else {
Node<T> current = getNode(index);
current.pre.next = current.next;
current.next.pre = current.pre;
size--;
}
}
// 刪除尾部元素
public void deleteTail() {
if (tail != null) {
tail = tail.pre;
if (tail != null) {
tail.next = null;
} else {//此時說明之前head和tail都指向唯一節點,連結串列刪除之後head和tail都應該指向null
head = null;
}
size--;
}
}
// 獲取指定位置的元素
public T get(int index) {
if (index < 0 || index >= size) {
throw new IndexOutOfBoundsException("Index is out of bounds");
}
Node<T> node = getNode(index);
return node.data;
}
// 獲取連結串列的大小
public int getSize() {
return size;
}
private Node<T> getNode(int index) {
if (index < 0 || index >= size) {
throw new IndexOutOfBoundsException("Index is out of bounds");
}
if (index < size / 2) {
Node<T> current = head;
for (int i = 0; i < index; i++) {
current = current.next;
}
return current;
} else {
Node<T> current = tail;
for (int i = size - 1; i > index; i--) {
current = current.pre;
}
return current;
}
}
private static class Node<T> {
T data;
Node<T> pre;
Node<T> next;
public Node(T data) {
this.data = data;
}
}
}
結語
在插入刪除的步驟,很多人可能因為繁瑣的過程而弄不明白,這個操作的寫法可能是多樣的,但本質操作都是一致的,要保證能成功表示節點並操作,這個可以畫個圖一步一步捋一下,看到其他不同版本有差距也是正常的。
還有很多人可能對一堆next.next搞不清楚,那我教你一個技巧,如果在等號右側,那麼它表示一個節點,如果在等號左側,那麼除了最後一個.next其他的表示節點。例如node.next.next.next可以看成(node.next.next).next。
在做資料結構與演演算法連結串列相關題的時候,不同題可能給不同節點去完成插入、刪除操作。這種情況操作時候要謹慎先後順序防止破壞連結串列結構。
演算法系列倉庫地址:https://github.com/javasmall/bigsai-algorithm