【scipy 基礎】--插值
插值運算是一種資料處理方法,主要用來填補資料之間的空白或缺失值。
因為在實際應用中,資料往往不是完整的,而是存在著空白或缺失值,這些空白或缺失值可能是由於資料採集困難、資料丟失或資料處理錯誤等原因造成的。
如果直接使用這些空白或缺失值進行分析和預測,將會對結果造成很大的影響。
插值運算可以用來填補這些空白或缺失值,從而恢復完整的資料集。
通過插值運算,可以估算出空白或缺失值的值,從而提高資料的完整性和準確性。
此外,插值運算還可以用來預測未來的資料趨勢或結果,對於資料分析和預測具有重要的意義。
本篇介紹Scipy為我們提供的插值處理方法。
1. 主要功能
Scipy中,關於插值的子模組是:scipy.interpolate。
其中又細分為:
| 類別 | 說明 |
|---|---|
| 單變數插值 | 主要包含interp1d等12個函數 |
| 多變數插值 | 主要包含griddata等11個函數 |
| 一維樣條函數 | 主要包含BSpline等16個函數 |
| 二維樣條函數 | 主要包含RectBivariateSpline等9個函數 |
| 其他函數 | 一些輔助計算的函數 |
插值效果的好壞,有個重要的因素在於是否根據資料的情況選擇了合適的插值演演算法。Scipy庫中已經實現的插值演演算法有:
- linear:線性插值演演算法
- nearest:最近鄰插值演演算法
- nearest-up:改進型最近鄰插值演演算法
- zero:零階樣條插值演演算法(等同於 previous)
- slinear:一階樣條插值演演算法(等同於 linear)
- quadratic:五階樣條插值演演算法
- cubic:三階樣條插值演演算法
- previous:前點插值演演算法
- next:後點插值演演算法
我們可以根據資料情況選擇合適的演演算法,下面用一些測試資料演示不同演演算法的插值效果:
from scipy.interpolate import interp1d
x = np.linspace(0, 20, 20)
y = x * np.cos(x)
plt.scatter(x,y)
plt.show()
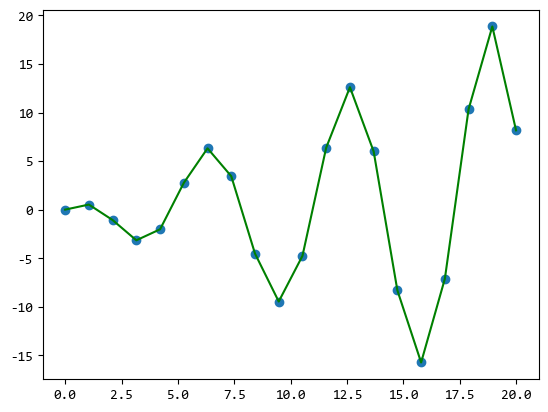
上圖是插值之前,直接由20個資料點連線起來的折線。
接下來,應用9種不同的插值演演算法將20個點補充為100個點,然後看看插值之後各種曲線的效果。
interp_types = [
"linear",
"nearest",
"nearest-up",
"zero",
"slinear",
"quadratic",
"cubic",
"previous",
"next",
]
fig = plt.figure(figsize=[12, 9])
fig.subplots_adjust(hspace=0.4)
for idx, typ in enumerate(interp_types):
f = interp1d(x, y, kind=typ)
x_dense = np.linspace(0, 20, 100)
y_dense = f(x_dense)
ax = fig.add_subplot(330 + idx+1)
ax.scatter(x, y)
ax.plot(x_dense, y_dense, color='g')
ax.set_title("插值演演算法-{}".format(typ))
plt.show()
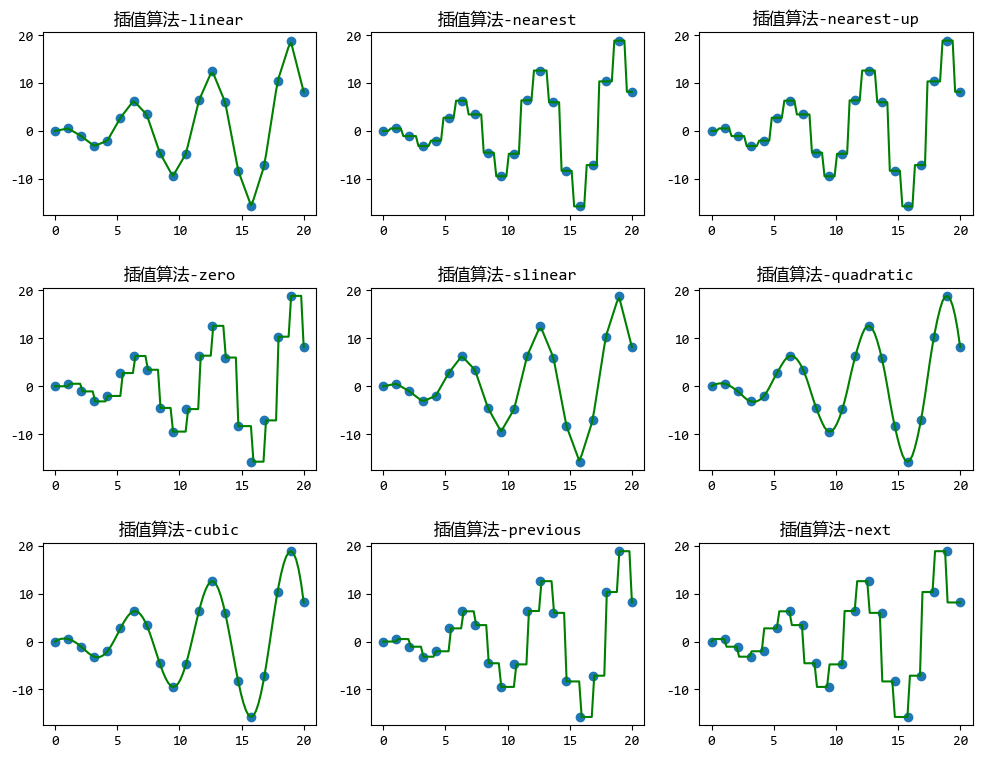
2. 一維插值範例
在我自己實際接觸的專案中,氣象資料的處理經常會用到插值。
因為氣象資料常常存在缺失值,這可能是由於感測器故障,資料傳輸問題,或者在某些情況下,由於天氣現象使得資料無法收集。
對於這些缺失值,我們可以使用Scipy的一維插值功能來進行填充。
比如下面是南京市某年的各個月的平均氣溫:
import pandas as pd
# 南京一年中每個月平均氣溫
df = pd.DataFrame({
"月份": ["一月", "二月", "三月",
"四月", "五月", "六月",
"七月", "八月", "九月",
"十月", "十一月", "十二月"],
"平均最低氣溫": [-1.6, 0.0, 4.4,
np.nan, 15.7, 20.4,
np.nan, 24.6, 19.1,
12.6, 6.1, -0.1],
"平均最高氣溫": [7.0, 8.4, np.nan,
20.1, 25.3, 29.0,
32.0, 32.2, 27.2,
np.nan, 16.9, 9.7],
})
df
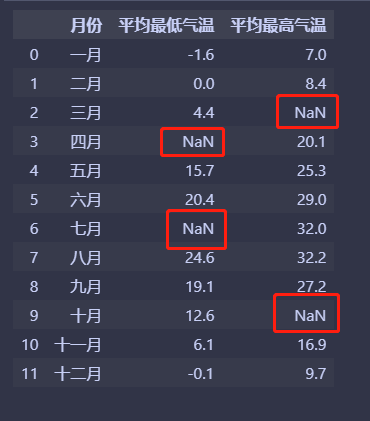
由於採集或者傳輸的原因,導致缺失了一些資料。
這樣的資料不僅繪製出來的折線圖會有斷開的地方,而且不利於後續的分析。
plt.plot(df["月份"], df["平均最低氣溫"], label="平均最低氣溫")
plt.plot(df["月份"], df["平均最高氣溫"], label="平均最高氣溫")
plt.legend()
plt.show()
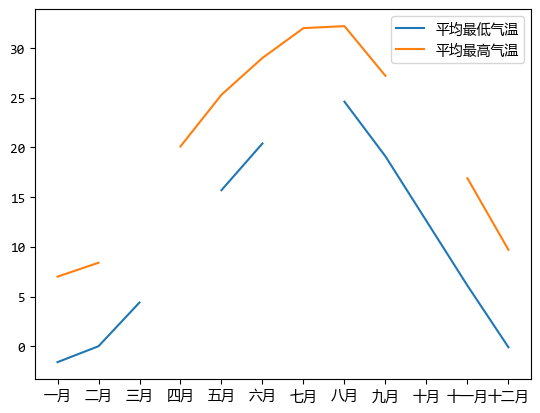
這時,可以用Scipy的插值演演算法來補充缺失資料。
from scipy.interpolate import interp1d
# 過濾掉缺失的 平均最低氣溫 資料
df_low =df[df["平均最低氣溫"].notna()]
# 根據已有的資料生成插值函數
f = interp1d(df_low.index, df_low["平均最低氣溫"], kind="cubic")
# 用插值函數補充缺失資料
df["平均最低氣溫"] = f(range(12))
# 平均最高氣溫 的缺失資料處理同上
df_high =df[df["平均最高氣溫"].notna()]
f = interp1d(df_high.index, df_high["平均最高氣溫"], kind="cubic")
df["平均最高氣溫"] = f(range(12))
df.round(1)
plt.plot(df["月份"], df["平均最低氣溫"], label="平均最低氣溫")
plt.plot(df["月份"], df["平均最高氣溫"], label="平均最高氣溫")
plt.legend()
plt.show()
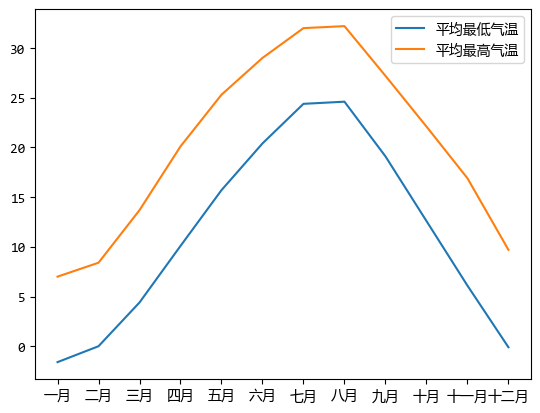
處理之後,資料的連續性更好了。
3. 二維插值範例
當自變數有2個的時候,就要用到二維插值了。
仍然以氣象上的資料舉例,上面範例是氣溫和時間的關係,我們把時間作為自變數,只要一維插值即可。
如果是和地點關聯的話,那麼地點作為自變數就有2個值(一般是經度和緯度)。
比如下面擷取了專案中一段降水量的資料:
# 資料是二維陣列:
# 每一行代表經度相同,緯度不同的地點
# 每一列代表緯度相同,經度不同的地點
data = np.array([
[9, 9, 5, 9, 10, 9, 8, 7, 11, 1],
[54, 36, 54, 32, 46, 51, 35, 33, 36, 11],
[35, 34, 34, 45, 52, 35, 34, 36, 41, 9],
[117, 112, 113, 133, 126, 127, 119, 96, 116, 23],
[110, 67, 91, 85, 94, 69, 77, 81, 65, 13],
[9, 7, 13, 12, 9, 6, 8, 9, 21, 3],
[50, 21, 24, 32, 36, 26, 28, 30, 24, 3],
[65, 41, 63, 67, 58, 50, 54, 45, 48, 16],
[36, 29, 32, 28, 38, 29, 41, 27, 29, 9],
[37, 61, 57, 35, 56, 51, 40, 58, 100, 34],
])
顯示降水量的分佈情況。
plt.imshow(data, cmap=plt.cm.GnBu)
plt.colorbar()
plt.xticks([])
plt.yticks([])
plt.show()
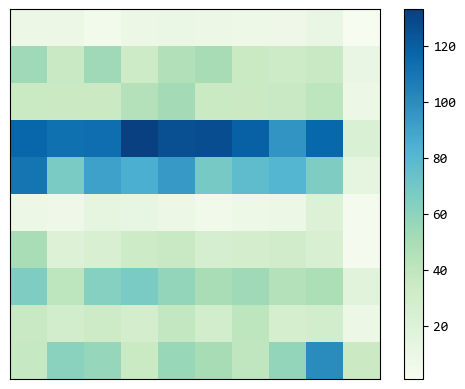
data中只有100個資料,所以每個格子一個值,看起來不是那麼連續,
而實際的降水情況不會像這樣離散的,區域之間的降水量應該是逐漸連續變化的。
所以,需要在data的基礎上進行二維插值:
from scipy.interpolate import RectBivariateSpline
# 原始資料是 10x10
x = np.linspace(0, 10, 10, endpoint=False)
y = np.linspace(0, 10, 10, endpoint=False)
# 插值後的資料是 500x500
x_new = np.linspace(0, 10, 500, endpoint=False)
y_new = np.linspace(0, 10, 500, endpoint=False)
# 從原始資料生成插值函數
f = RectBivariateSpline(x, y, data.T)
# 用插值函數計算新的資料
data_new = f(x_new, y_new)
# 顯示插值後的結果
plt.imshow(data_new.T, cmap=plt.cm.GnBu)
plt.colorbar()
plt.xticks([])
plt.yticks([])
plt.show()

這是插值到 500x500 的效果,值越大,連續性越好。
有興趣的話,可以調整上面程式碼中 x_new 和 y_new 的個數,看看不同的效果。
4. 總結
插值作為一種常見的資料處理方法,應用的領域和場景非常多,比如:
- 資料預測:通過插值技術,可以預測未來的資料趨勢或結果。
- 影象處理:插值可以用於影象處理和影象分析,以提高影象的解析度或質量。
- 機器學習:插值技術也可以用於機器學習和人工智慧領域。用於構建迴歸模型或分類模型,以便對未知資料進行預測或分類。
本文主要介紹了Scipy庫的插值子模組,其內建的插值演演算法,以及兩個應用插值的小例子。