傅立葉變換是一種數學變換，它可以將一個函數或訊號轉換為另一個函數或訊號，它可以將時域訊號轉換為頻域訊號，也可以將頻域訊號轉換為時域訊號。
在很多的領域都有廣泛的應用，例如訊號處理、通訊、影象處理、電腦科學、物理學、生物學等。

它最大的功能是能夠分析和提取訊號的特徵，將複雜的訊號分解為簡單的訊號。
有人甚至說傅立葉變換是一種可以讓我們看透世界本質的變換，將紛繁世界的表象中的本質顯現出來。

1. 簡介

從數學的角度來推導傅立葉變換的話，會涉及到很多的基本的數學概念，比如正交基，級數，正弦餘弦函數等等。
這裡主要是為了看懂和使用傅立葉變換，瞭解傅立葉變換中的主要概念即可，
Scipy庫會幫助我們處理其中的細節。

舉例來說，對於現實中遇到的如下一個原始訊號（一般都是非週期性且無規律的）：

這樣的訊號，可以是聲音，可以是氣溫變化，可以是心電圖，甚至可以是股票漲跌情況等等。

原始的訊號變化複雜，而且大部分情況都看不出什麼規律。
這時，傅立葉變換就能發揮作用了，它能夠將複雜無序的訊號轉換為一系列簡單規則的訊號。
比如上面的訊號轉換之後變成下面6個簡單的訊號：

另外，傅立葉變換是可逆的，它也能夠將變換後的多個簡單的訊號還原成原始的複雜訊號。

2. fft 模組

Scipy中處理傅立葉變換有2個子模組：fft和fftpack。
fftpack即將被淘汰，所以儘量使用fft模組。

fft模組中，傅立葉變換的主要函數有：

函數名	說明
fft	計算一維離散傅立葉變換
ifft	計算一維離散傅立葉逆變換
fft2	計算二維離散傅立葉變換
ifft2	計算二維離散傅立葉逆變換
fftn	計算N維離散傅立葉變換
ifftn	計算N維離散傅立葉逆變換

2.1. 變換範例

建立一個複合的訊號：

import numpy as np
import matplotlib.pyplot as plt

# 生成 0~8pi 之間100個點
x = np.linspace(0, 8*np.pi, 100)

# 隨便生成6個不同的正弦訊號
y1 = np.sin(x)
y2 = 4*np.sin(2*x)
y3 = 2*np.sin(4*x)
y4 = 8*np.sin(0.3*x)
y5 = 6*np.sin(0.8*x)
y6 = 0.5*np.sin(5*x)

y = y1 + y2 + y3 + y4 + y5 + y6

plt.plot(x, y)
plt.show()

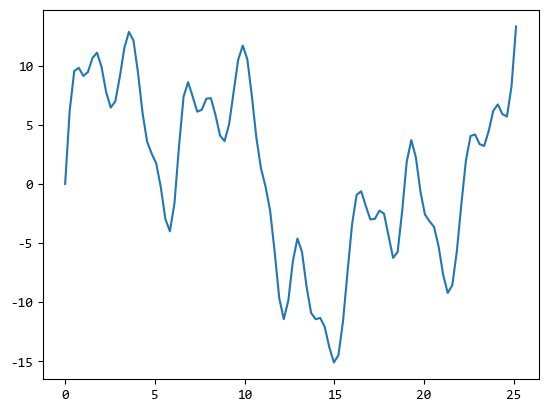
下面通過一維傅立葉變換，看看得到的結果：

from scipy import fft as spfft

fft_result = spfft.fft(y)
print(fft_result.shape)
# 執行結果
(100,)

fft_result[1:11]
# 執行結果（顯示前10個，總共100個）
array([ 99.548317    -0.j        , 273.43743482-274.69892934j,
       -10.91586207 +66.24943608j, 167.24328363-151.29814008j,
       -57.93543536 +49.80593353j, -30.50244642 +56.21303872j,
       -19.99077861 +37.24642604j, -13.54997057 +21.30562857j,
        35.119202  -161.91923934j, -17.17382544 +41.98143084j])


fft_result[-10:]
# 執行結果（顯示後10個，總共100個）
array([-13.61273919 -29.66475047j, -17.17382544 -41.98143084j,
        35.119202  +161.91923934j, -13.54997057 -21.30562857j,
       -19.99077861 -37.24642604j, -30.50244642 -56.21303872j,
       -57.93543536 -49.80593353j, 167.24328363+151.29814008j,
       -10.91586207 -66.24943608j, 273.43743482+274.69892934j])

觀察快速傅立葉轉換之後得到的結果：

轉換的結果中，每個元素都是複數
前10個元素中，除去第一個，剩下的元素和後10個元素相比，實部相同，虛部相反

傅立葉變換之後，可以得到兩個描述訊號的圖形：

頻譜圖：各個頻率的波的振幅資訊
相點陣圖：各個頻率的波的相位資訊，相位就是波在特定時間所處的位置

頻譜資訊可以通過 np.abs 方法計算得出：

fig = plt.figure(figsize=[8,4])
ax1 = fig.add_subplot(121) 
data = np.abs(fft_result)
ax1.plot(data)
ax1.set_title("雙邊頻譜圖")

ax2 = fig.add_subplot(122) 
data = np.abs(fft_result[:50])
ax2.plot(data)
ax2.set_title("單邊頻譜圖")

plt.show()

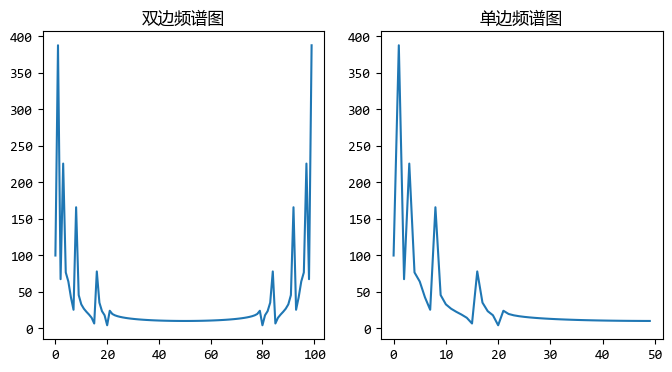
相位資訊可以通過 np.angle 方法計算得出：

fig = plt.figure(figsize=[8,4])
ax1 = fig.add_subplot(121) 
data = np.angle(fft_result)
ax1.plot(data)
ax1.set_title("雙邊相點陣圖")

ax2 = fig.add_subplot(122) 
data = np.angle(fft_result[:50])
ax2.plot(data)
ax2.set_title("單邊相點陣圖")

plt.show()

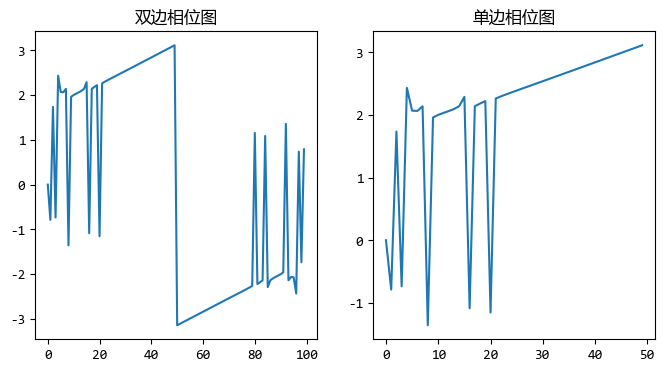
從這兩個圖中就能得變換後各個頻率的訊號的頻率，振幅，相位資訊。

2.2. 逆變換範例

逆變換就是將變換後的訊號還原為原始訊號。

因為傅立葉變換並沒有任何資訊的損失，所以逆變換之後可以看出訊號的波形沒有任何改變。

data = spfft.ifft(fft_result)

# 逆變換之後，忽略虛部的數位
plt.plot(x, np.real(data))
plt.show()

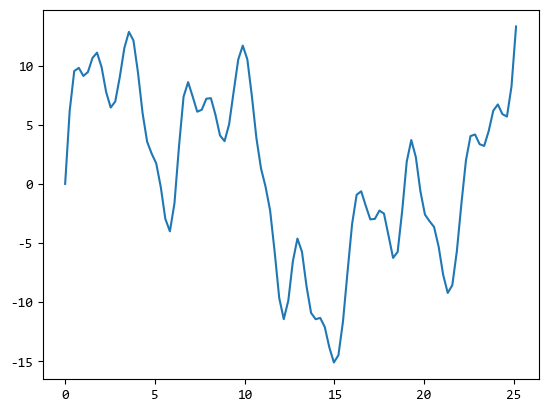
3. 應用

最後，利用傅立葉變換，我們試著做一個改變聲音效果的小例子。

首先，讀取一段音訊，Scipy就可以直接讀取wav檔案。

import scipy.io.wavfile as wav

# 讀取音訊，返回取樣率和取樣的數值
rate, all_samples = wav.read("/path/to/fft-test.wav")
print(rate)
print(all_samples[1000:1010])
# 執行結果
16000
[122 133 149 151 165 151 160 159 155 151]

plt.plot(all_samples)
plt.show()

音訊檔是網上隨便找的一段英語對話。

接著，對讀取的訊號做傅立葉變換，觀察變換後的結果：

dd = spfft.rfft(all_samples)
plt.plot(np.abs(dd))
plt.show()

注意，這裡用了 rfft函數，不是之前的fft函數，
兩者的區別在於fft的結果是複數，會形成對稱的雙邊圖，就像上一節介紹的那樣。
而rfft的結果是實數，且是單邊的，如上圖所示。

這兩個函數根據實際情況選擇使用，都可以對訊號進行傅立葉變換。
因為我後面的處理不需要雙邊的資訊，所以這裡用 rfft 函數來做傅立葉變換。

3.1. 處理一

第一種處理，我嘗試把頻率20000HZ以上的訊號都去掉，看看音訊的效果有什麼變化。

new_data = dd.copy()
# 20000HZ以上頻率的資料設為0
new_data[20000:] = 0

fig = plt.figure(figsize=[8,4])
ax1 = fig.add_subplot(121) 
ax1.plot(np.abs(new_data))

ax2 = fig.add_subplot(122) 
ax2.plot(np.abs(dd))

plt.show()

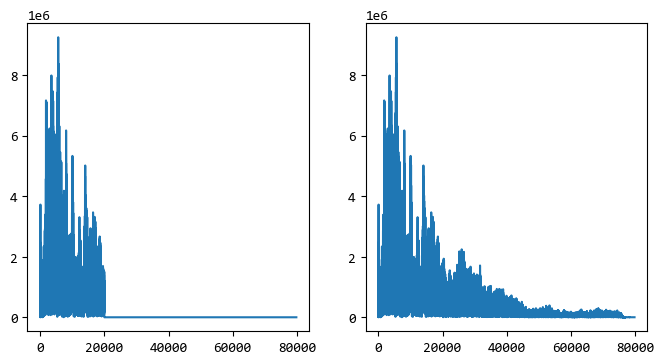
處理之後的訊號逆變換為原始訊號，再儲存為wav音訊檔，看音訊的變化效果。

new_data = spfft.irfft(new_data)
new_data = np.rint(new_data)
new_data = new_data.astype("int16")

wav.write("/path/to/fft-test-1.wav", rate, new_data)

轉換後的音訊和原音訊比，聽起來聲音更加悶一些，模糊一些。

3.2. 處理二

這次與處理一相反，把20000HZ以下的訊號去掉。

new_data = dd.copy()
# new_data[20000:] = 0
new_data[:20000] = 0

fig = plt.figure(figsize=[8,4])
ax1 = fig.add_subplot(121) 
ax1.plot(np.abs(new_data))

ax2 = fig.add_subplot(122) 
ax2.plot(np.abs(dd))

plt.show()

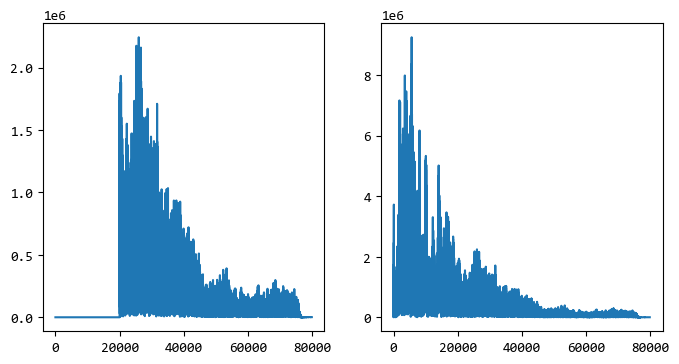
然後同樣的把訊號逆變換回去，並儲存為wav檔案。

new_data = spfft.irfft(new_data)
new_data = np.rint(new_data)
new_data = new_data.astype("int16")

wav.write("/path/to/fft-test-2.wav", rate, new_data)

這次的聲音聽起來很遙遠，像是長途電話的感覺。

4. 總結

本篇主要介紹了傅立葉變換是什麼，以及如何使用Scipy庫來進行傅立葉變換。
目的是瞭解和使用傅立葉變換，而不是從數學角度去推導傅立葉變換。

最後的小例子雖然簡單，但見微知著，僅僅刪除了一些頻率的訊號，聲音效果就隨之變化。
如果把不同聲音的檔案中，影響音調，音色的頻率分析出來，就可以製作一個變聲器，
把自己的聲音變成男聲女聲，兒童老人等等。

進一步，用二維傅立葉變換的話，可以分析影象，把影象中的主要頻率找出來，
深入下去既可以做影象修復，也可以做影象識別等等。

Scipy庫中還有多維傅立葉變換，可以分析現實情況下更加複雜的訊號。

5. 附錄

文中用到的完整程式碼（ipynb格式）和一個音訊檔，可以從下面的地址下載：
scipy-fft-sample.zip:
https://url11.ctfile.com/f/45455611-910542660-6d7e0f?p=6872
(存取密碼: 6872)

【scipy 基礎】--傅立葉變換