games101-1 光柵化與光線追蹤中的空間變換
在學習了一些games101的課程之後,我還是有點困惑,對於計算機圖學的基礎知識,總感覺還是缺乏一些更加全面的認識,幸而最*在做games101的第五次作業時,查詢資料找到了scratchpixel這個網站,看了一些文章,終於把腦子裡的一團亂麻組織起來了,也就有了這篇關於圖學的第一篇部落格。
想要更好的理解這篇部落格,強烈推薦先學習games101中關於transformation,rasterization和ray tracing的第一部分
以下內容參考:https://www.scratchapixel.com/lessons/3d-basic-rendering/computing-pixel-coordinates-of-3d-point/perspective-projection.html
https://www.scratchapixel.com/lessons/3d-basic-rendering/computing-pixel-coordinates-of-3d-point/mathematics-computing-2d-coordinates-of-3d-points.html
https://www.scratchapixel.com/lessons/3d-basic-rendering/ray-tracing-generating-camera-rays/generating-camera-rays.html
如果內容有誤,歡迎指出
光柵化與光線追蹤的理解
在圖學中一個很重要的問題就是,我們如何把一個三維空間中的物體,去展示到一個二維*面上。
這件事其實我們可以分成兩步去做,第一步是解決visibility的問題,第二步是解決shading的問題。
怎麼理解這兩種方法呢?我們先想象,現在在一個無窮大的場景裡面,有很多物體,還有一個攝像機,攝像機面前一定距離有個*面,現在我們想知道通過攝像機在它面前這個二維*面上看到的所有三維物體的形象。
光柵化方法,就是把場景內的所有物體先都投影到這個*面上,然後進行著色shading,這裡就是光柵化比較麻煩的地方,我們需要設計著色模型(games101中的bling-phone模型),考慮到物體的空間先後順序我們需要z-buffer,考慮到陰影效果我們需要shadow map,以及紋理貼圖來幫助我們。
而光線追蹤,模擬了光線在場景中的傳播,在光線追蹤中,從觀察點(或相機)出發的光線被跟蹤以確定它們與場景中的物體相交點,然後計算反射、透射和光照等效果,是一種基於物理的渲染方法。
通過上述描述,我們可以發現光柵化可以短時間內處理大量物體,但在光照效果等方面不如光線追蹤,而光線追蹤速度較慢,因為需要考慮到光線的種種複雜的傳播情況,這也就導致光柵化主要用於實時渲染,而光線追蹤主要用於離線渲染
我們再來考慮針對這兩種方法的空間變換,我們會發現這兩種方法其實在幹相反的事情,光柵化的座標變換是把三維變二維,光線追蹤是需要攝像機到*面上每個畫素點連線的光線,然後求光線與物體的交點,實際上需要我們把二維的點轉換為三維,具體的過程我們在接下來的部分闡述
不同空間的介紹
要理解光柵化與光線追蹤的空間變換,我們首先要搞清楚幾個空間的定義
世界空間:世界空間就是我們之前提到的無窮大的場景,所有的點的定義最初都是在這個三維空間中,與之對應的是世界座標系
相機空間:相機空間就是以相機為座標原點的座標系建立的空間,我們可以使用games101中提到的camera transformation對應的矩陣,實現世界座標系到相機座標系之間的轉換,一般來說,我們的相機的位置在(0,0,0)這個座標原點,朝向世界座標系的-z方向。
螢幕空間:螢幕空間是一個二維空間,相機空間中的點經過透視變換可以到image plane上,然後我們根據畫布(canvas)的範圍,可以在image plane這個無窮大的*面上劃分出螢幕空間

NDC空間:把螢幕空間座標系標準化到【0-1】的空間中
柵格空間:NDC空間中的2D點被轉換為2D畫素座標,為此,我們將標準化點的 x 和 y 座標乘以畫素寬度和高度,從 NDC 到柵格空間還需要反轉該點的 y 座標。 由於畫素座標是整數,因此最終座標需要四捨五入到最接*的以下整數。
下面的圖很形象地展示了上面的三個空間的區別:

其實我們電腦的螢幕就相當於柵格空間,不同的解析度代表著不同的水*畫素數與豎直畫素數,也就代表著不同的畫素寬度與高度,代表著不同的柵格空間計算方法
注意我們這裡的討論實際上簡化了螢幕座標系與NDC座標系,games101中的投影變換實際上就是直接從相機空間變換到了NDC空間或者說變換到了裁剪空間然後經過齊次除法到NDC空間,空間是三維的,因為我們不僅要完成投影,還需要記錄點的z座標資訊來進行深度快取等等,確定物體的先後關係:

可以看到二維空間與三維空間的區別就是二維空間捨棄了z座標,它們在xy座標方面做的都是投影,三維空間相當於多做了z座標的投影
注意games101其實並沒有過多的討論裁剪空間,而是推導了一個矩陣直接轉換到NDC空間,這也是未來部落格中要探討的內容,同時z-fighting的現象也未提及(*遠*面距離過大導致的問題)
在我們這裡的討論螢幕座標系與NDC座標系是二維的,這樣可以把光柵化與光線追蹤的visibility處理統一起來,因為光線追蹤中我們並不需要使用投影矩陣,就不存在光柵化中的視錐體與立方體,只需要二維的螢幕空間。
光柵化做的就是從世界空間到柵格空間,實現每個物體的visibility,然後著色
而光線追蹤做的是實現每個光線的視覺化,然後著色,需要我們從柵格空間轉換到世界空間。
光柵化中的空間變換
世界空間到觀察空間或者說是攝像機空間:
這一步很簡單,和games100課程中的一樣,實際上就是進行座標系變換,進行旋轉與*移,值得注意的是預設,相機正對的是z的負半軸,所以我們可見的物體的z座標也是負的
那麼在進行從觀察空間到螢幕空間的過程中,我們要進行投影,將3維的點投影到2維的螢幕上:
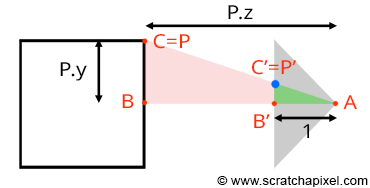
這樣我們根據相似關係,可以得到螢幕空間與觀察空間的xy座標對映,注意這裡我們假設和**面的距離是1,可以得到:
\(\begin{array}{l} P'.x = \dfrac{P_{camera}.x}{P_{camera}.z}\\ P'.y = \dfrac{P_{camera}.y}{P_{camera}.z}. \end{array}\)
但是注意我們之前提到過物體的z座標是負的,所以這樣進行除法會導致xy發生顛倒,因此,我們要再加上負號:
\(\begin{array}{l} P'.x = \dfrac{P_{camera}.x}{-P_{camera}.z}\\ P'.y = \dfrac{P_{camera}.y}{-P_{camera}.z}. \end{array}\)
之前提到過螢幕空間是有範圍的,由寬度與高度決定,所以我們要加上這個限制
\(\text {visible} = \begin{cases} yes & |P'.x| \le {W \over 2} \text{ or } |P'.y| \le {H \over 2}\\ no & \text{otherwise} \end{cases}\)
從螢幕空間到NDC空間,需要我們把原來在[-width/2]--[width/2]和[-height/2]到[height/2]之間的點轉換到[0-1]的點(有的NDC空間採用的是[-1-1]):
\(\begin{array}{l} P'_{normalized}.x = \dfrac{P'.x + width / 2}{ width }\\ P'_{normalised}.y = \dfrac{P'.y + height / 2}{ height } \end{array}\)
從NDC空間到柵格空間,我們需要乘以畫素寬度與高度,因為我們認為畫素點是一個個小矩形來進行柵格化,並且取整,這一步也被稱為viewport變換
\(\begin{array}{l} P'_{raster}.x = \lfloor{ P'_{normalized}.x * \text{ Pixel Width} }\rfloor\\ P'_{raster}.y = \lfloor{ P'_{normalized}.y * \text{Pixel Height} }\rfloor \end{array}\)
同時我們注意到柵格空間的y是向下的,所以改變方向取反:
\(\begin{array}{l} P'_{raster}.x = \lfloor{ P'_{normalized}.x * \text{ Pixel Width} }\rfloor\\ P'_{raster}.y = \lfloor{ (1 - P'_{normalized}.y) * \text{Pixel Height} }\rfloor \end{array}\)
以上我們就將三維空間中的點視覺化到了二維空間中
光線追蹤中的空間變換
針對光線追蹤,我們需要的是視覺化我們的光線,因為我們需要實際計算光線與物體相交,所以我們的光線需要世界座標下的三維表示,簡單來說一個光線可以如下定義:

我們已經知道了O的位置,它就是座標原點(0,0,0)
現在需要知道P的位置
現在考慮下面這張圖:

第一步轉換到NDC空間:
\(\begin{array}{l}
PixelNDC_x = \dfrac{(Pixel_x + 0.5)}{ImageWidth},\\
PixelNDC_y = \dfrac{(Pixel_y + 0.5)}{ImageHeight}.
\end{array}\)
注意這裡我們只考慮光線穿過畫素點的中心,所以我們要加上0.5,然後再分別除以柵格空間的寬度與高度
第二步轉換到螢幕空間:
注意螢幕空間的y軸發生了反轉,同時由於我們是將原本的影象壓縮到了-1-1的這個空間中,所以我們現在要將其還原回去,即寬度從[-1--1]轉換成[-width/2---width/2],高度同理,我們使用寬高比以及fov角度來表示就可以得到:
\(\begin{array}{l} PixelCamera_x = (2 * {PixelNDC_x } - 1) * ImageAspectRatio * tan(\dfrac{\alpha}{2}),\\ PixelCamera_y = (1 - 2 * {PixelNDC_y }) * tan(\dfrac{\alpha}{2}). \end{array}\)
其中tan(a/2)表示影象高度的一半,因為我們在這裡假設**面座標是-1
最後轉換到世界空間中,只需要加入z座標-1,然後從相機空間轉換到世界空間即可
上述過程也就是games101第五次作業求光線的實現