splay + 垃圾回收 知識點與例題的簡要講解
splay 簡要講解
前置芝士:普通二元樹
splay tree是一個越處理越靈活的資料結構,通過splay(伸展)操作,使整棵樹的單次查詢時間複雜度接近於O(log n),整棵樹的高度也接近於log n
根據上面的這句話,很明顯能看出splay與普通二元樹的區別
普通二元樹經過多次處理後,很容易退化成鏈,單次查詢的複雜度直升O(n),對於處理大型資料來說,這是絕對不能允許的
OI和ACM界也經常會有資料能使一個普通二元樹快速退化成鏈
例: 1 - 2 - 3 - 4 - 5 - 6 - 7 - 8 - 9
很明顯,對於大型資料的處理來說,普通二元樹已經滿足不了了
下面,我將會以例圖來講解中序遍歷
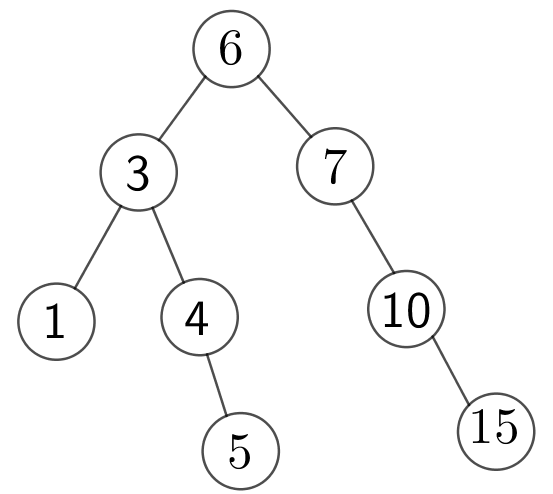
這張圖是我偷的,哈哈
在這組資料中,數的根節點為6,整棵樹的中序遍歷為1,2,3,4,5,6,7,10,15,一個樹的中序遍歷為:左子樹 + 根 + 右子樹
很明顯,這是遞增的,當前這個splay樹維護的是一個遞增的序列
________________________________
操作
_______________
splay 有一個核心操作,就叫splay(伸展)
splay操作是依靠rotate去實現的
rotate(x) 點x向上翻轉,分左旋和右旋,使其中序遍歷不變,詳情見程式碼
(關鍵是將這玩意得要圖,要不不好講清,如果程式碼看不懂的話,點這裡,至OI wiki)splay(x,k) 將點x翻轉到點k的下方,每次新增一個數,就將其splay到根節點的下方(每次翻轉的複雜度為log n),這樣的話就能使整棵樹的高度接近於log n
-------------------------------
在樹中每個點的前繼(succ)就是其在陣列中的上一個點,後繼(pred)就是下一個點,
kth 查詢第k大的數,在樹中每個點的前繼就是其在陣列中的上一個點,後繼就是下一個點,所以在其中序遍歷有序的前提下,遞迴判斷每個子樹的大小就行了
當然,p2042這道題的kth是第k個數,並不是第k大的數,因為這道題(p2042)維護的是一個區間
---------
build(or insert) 建立子樹(或插入一個數)
如果我們要建立一段數位,插入到下標x的後面,想一下,是不是可以先在這組將要插入的數中建樹,然後直接將這個樹插到下標為x的右子樹下,是不是就可以了?
同樣,insert(x)也是同理,只不過是其子樹的大小隻有1
---------
detele操作,垃圾回收
每一次delete(x)後,tree[x]這個點為空,是不是浪費了?這很不符合我們環保的心理 (=_=) ,所以在每次我們delete操作後,將其節點下標儲存下來,到build(or insert)的時候再使用,這樣是不是就做到回收再利用了?
---------------
當我們想要處理區間 [x,y] 的時候,記住無論我們怎麼splay,其中序遍歷一定不變,再想想,在splay中一個點的前繼和後繼是什麼
所以我們就可以現將x splay到根節點的下方,將y splay到x的下方,其 [x,y] 是不是就是點x及其右子樹 和 點y及其左子樹,然後就可以區間處理了
___________________________________________
記住,splay所維護的可以不是一個陣列的val值,他可以是陣列的下標
___________________________________________
一切盡在註釋之中,這道題所維護的是每一個點的下標,並不是其點的val
例題:P2042 [NOI2005] 維護數列
splay+垃圾回收 #include"bits/stdc++.h" using namespace std; const int N = 500010,INF = 1e9; #define inl inline #define reg register //#define ll long long int n,m; struct node { int s[2],p,v; int rev,same,size,sum,ms,ls,rs; //翻轉標記,相同標記,子樹大小,區間和,最大子段和,最大字首和,最大字尾和 inl void init(int _v,int _p) //預處理 { s[0] = s[1] = 0,p = _p,v = _v; rev = same = 0; size = 1,sum = ms =v; ls = rs = max(v,0); } }tr[N]; int root; int nodes[N],tt;//垃圾回收陣列,tt為其大小 int w[N]; inl void pushup(int x) //向上傳遞 { auto &u = tr[x],&l = tr[u.s[0]],&r = tr[u.s[1]]; u.size = l.size + r.size + 1; u.sum = l.sum + r.sum + u.v; u.ls = max(l.ls,l.sum + u.v + r.ls); u.rs = max(r.rs,r.sum + u.v + l.rs); u.ms = max(max(l.ms,r.ms),l.rs + u.v + r.ls); //處理各個資料
} inl void pushdown(int x) //向下傳遞 { auto &u = tr[x],&l = tr[u.s[0]], &r = tr[u.s[1]]; if(u.same) //若有相同標記,則翻轉標記就並不需要 { u.same = u.rev = 0; if(u.s[0]) l.same = 1,l.v = u.v,l.sum = l.v * l.size; if(u.s[1]) r.same = 1,r.v = u.v,r.sum = r.v * r.size;
if(u.v > 0) { if(u.s[0]) l.ms = l.ls = l.rs = l.sum; if(u.s[1]) r.ms = r.ls = r.rs = r.sum; }else { if(u.s[0]) l.ms = l.v,l.ls = l.rs = 0; if(u.s[1]) r.ms = r.v,r.ls = r.rs = 0; }
//左右子樹資料處理 }else if(u.rev) { u.rev = 0,l.rev ^= 1,r.rev ^= 1; swap(l.ls,l.rs),swap(r.ls,r.rs); swap(l.s[0],l.s[1]),swap(r.s[0],r.s[1]);
//翻轉 } } inl void rotate(int x) { int y = tr[x].p,z = tr[y].p; int k = tr[y].s[1] == x; tr[z].s[tr[z].s[1] == y] = x,tr[x].p = z; tr[y].s[k] = tr[x].s[k ^ 1],tr[tr[x].s[k ^ 1]].p = y; tr[x].s[k ^ 1] = y,tr[y].p = x; pushup(y),pushup(x);
//向上旋轉 } inl void splay(int x,int k) { while (tr[x].p != k) { int y = tr[x].p, z = tr[y].p; if (z != k) if ((tr[y].s[1] == x) ^ (tr[z].s[1] == y)) rotate(x); else rotate(y); rotate(x); } if (!k) root = x; }
//伸展 inl int get_k(int k) //查詢第k個數 { int u = root; while (u) { pushdown(u); if (tr[tr[u].s[0]].size >= k) u = tr[u].s[0]; else if (tr[tr[u].s[0]].size + 1 == k) return u; else k -= tr[tr[u].s[0]].size + 1, u = tr[u].s[1]; } } inl int build(int l,int r,int p) //建造子樹 { int mid = l + r >> 1; int u = nodes[tt -- ]; tr[u].init(w[mid], p); if (l < mid) tr[u].s[0] = build(l, mid - 1, u); if (mid < r) tr[u].s[1] = build(mid + 1, r, u); pushup(u); return u; } inl void dfs(int u) //delete 操作 { if(tr[u].s[0]) dfs(tr[u].s[0]); if(tr[u].s[1]) dfs(tr[u].s[1]); nodes[ ++ tt] = u; //垃圾回收
} int main(void) { for(int i = 1;i < N;i ++) nodes[ ++ tt] = i; //nit [1,n] -> 垃圾回收站 scanf("%d%d",&n,&m); tr[0].ms = -INF; w[0] = w[n+1] = -INF; for(int i = 1;i <= n;i ++) scanf("%d",&w[i]); root = build(0,n + 1,0); char op[20]; while (m -- ) { scanf("%s", op); if (!strcmp(op, "INSERT")) { int posi, tot; scanf("%d%d", &posi, &tot); for (int i = 0; i < tot; i ++ ) scanf("%d", &w[i]); int l = get_k(posi + 1), r = get_k(posi + 2); splay(l, 0), splay(r, l); int u = build(0, tot - 1, r); tr[r].s[0] = u; pushup(r), pushup(l); } else if (!strcmp(op, "DELETE")) { int posi, tot; scanf("%d%d", &posi, &tot); int l = get_k(posi), r = get_k(posi + tot + 1); splay(l, 0), splay(r, l); dfs(tr[r].s[0]); tr[r].s[0] = 0; pushup(r), pushup(l); } else if (!strcmp(op, "MAKE-SAME")) { int posi, tot, c; scanf("%d%d%d", &posi, &tot, &c); int l = get_k(posi), r = get_k(posi + tot + 1); splay(l, 0), splay(r, l); auto& son = tr[tr[r].s[0]]; son.same = 1, son.v = c, son.sum = c * son.size; if (c > 0) son.ms = son.ls = son.rs = son.sum; else son.ms = c, son.ls = son.rs = 0; pushup(r), pushup(l); } else if (!strcmp(op, "REVERSE")) { int posi, tot; scanf("%d%d", &posi, &tot); int l = get_k(posi), r = get_k(posi + tot + 1); splay(l, 0), splay(r, l); auto& son = tr[tr[r].s[0]]; son.rev ^= 1; swap(son.ls, son.rs); swap(son.s[0], son.s[1]); pushup(r), pushup(l); } else if (!strcmp(op, "GET-SUM")) { int posi, tot; scanf("%d%d", &posi, &tot); int l = get_k(posi), r = get_k(posi + tot + 1); splay(l, 0), splay(r, l); printf("%d\n", tr[tr[r].s[0]].sum); } else printf("%d\n", tr[root].ms); //MAX-SUM } return 0; } /*
輸入樣例 1
9 8 2 -6 3 5 1 -5 -3 6 3 GET-SUM 5 4 MAX-SUM INSERT 8 3 -5 7 2 DELETE 12 1 MAKE-SAME 3 3 2 REVERSE 3 6 GET-SUM 5 4 MAX-SUM */
可能對於剛剛學習splay的人來說,這道題明顯有點難了
點這裡,來做P3224 [HNOI2012] 永無鄉答案我放在這裡了,這道題維護的是數位的val
這道題用了並查集的啟發式合併,說白了就是在合併操作中將較小的集合合併到較大的集合中,以減少所浪費的時間
為什麼要用啟發式合併?合併操作不是O(1)嗎?
不不不,這道題是並查集維護每個splay,splay的合併是O(log n),並不是O(1),需要啟發式合併,來過毒瘤資料
#include"bits/stdc++.h" using namespace std; const int N = 500010; #define inl inline #define reg register //#define ll long long int n,m; struct node { int s[2],p,v,id; int size; inl void init(int _v,int _id, int _p) { v = _v,id = _id,p = _p; size = 1; } }tr[N]; int root[N],idx; int p[N]; inl void read() { std::cin.tie(nullptr); } inl int Find(int x) { return p[x] != x ? p[x] = Find(p[x]) : p[x]; } inl void pushup(int x) { tr[x].size = tr[tr[x].s[0]].size + tr[tr[x].s[1]].size + 1; } inl void rotate(int x) { //y為x的父節點,z為x的爺節點 int y = tr[x].p,z = tr[y].p; int k = tr[y].s[1] == x;//k為(x是否為y的右節點)//即k為(x節點的左右兒子) tr[z].s[tr[z].s[1] == y] = x,tr[x].p = z; //z節點的y兒子改為x兒子,x節點的父節點改為z tr[y].s[k] = tr[x].s[k ^ 1],tr[tr[x].s[k ^ 1]].p = y; //處理原x的右兒子,以及原x右節點的parent tr[x].s[k ^ 1] = y,tr[y].p = x; //更改原x的非y兒子節點(另一個兒子),更改y的父節點為x pushup(y),pushup(x); //update size //x上移1個單位 } inl void splay(int x,int k,int b)//將集合b的splay中x節點轉到k節點的下面while(tr[x].p != k) { int y = tr[x].p, z = tr[y].p; if(z != k) if((tr[y].s[1] == x) ^ (tr[z].s[1] == y)) rotate(x); else rotate(y); //雙旋 rotate(x); } //k==0 if(!k) root[b] = x;//集合b的根節點為x } inl void insert(int v,int id,int b)//將編號為id,重要度為v 的節點加入集合b的splay中 { reg int u = root[b],p = 0; while(u) p = u,u = tr[u].s[v > tr[u].v]; u = ++idx; if(p) tr[p].s[v > tr[p].v] = u; tr[u].init(v,id,p); splay(u,0,b); } inl void dfs(int u,int b)//將根節點u所在splay中的每一個點插入到集合b的splay中 { if(tr[u].s[0]) dfs(tr[u].s[0],b); if(tr[u].s[1]) dfs(tr[u].s[1],b); insert(tr[u].v,tr[u].id,b);//查詢集合b的splay中重要度第k小的節點編號 } inl int get_k(int k,int b)//²éѯ¼¯ºÏbµÄSplayÖÐÖØÒª¶ÈµÚkСµÄ½Úµã±àºÅ { int u = root[b]; while(u) { if(tr[tr[u].s[0]].size >= k) u = tr[u].s[0]; else if(tr[tr[u].s[0]].size + 1 == k) return tr[u].id; else k -= tr[tr[u].s[0]].size + 1,u = tr[u].s[1]; } return -1; } int main(void) { read(); scanf("%d%d",&n,&m); //init Find-Union and root for(int i = 1;i <= n;i ++) { p[i] = root[i] = i; int v; scanf("%d",&v); tr[i].init(v,i,0);/init 每個集合的root } idx = n;//前n個下標個n個splay的根節點用 while(m--) { int a,b; scanf("%d%d",&a,&b); a = Find(a),b = Find(b); if(a != b)//如果兩個島不在一個集合中,需要合併 { /* tr[root[a]].size > tr[root[b]].size
保證集合a中元素的個數 <= 集合b中元素的個數
啟發式合併
保證較小的集合加入較大的集合 */ if(tr[root[a]].size > tr[root[b]].size) swap(a,b);//保證集合a中的元素個數 <= 集合b中的元素個數 dfs(root[a],b);//將集合a的splay裡的每一個點插入到集合b的splay裡面 p[a] = b;//將集合a合併入集合b } } reg int q; scanf("%d",&q); while(q --) { char op[2]; int a,b; scanf("%s%d%d",op,&a,&b); if(*op == 'B')//add edge { a = Find(a),b = Find(b); if(a != b)//Union 如果兩個島不在一個集合裡,需要合併 { if(tr[root[a]].size > tr[root[b]].size) swap(a,b); dfs(root[a],b); p[a] = b; } }else { a = Find(a);//集合中不足b個數,輸出"-1" if(tr[root[a]].size < b) puts("-1"); else printf("%d\n",get_k(b,a));//否則查詢第k小數 } } return 0; }
好了,就到這裡了
資料結構不能單純靠記憶,一定要理解,記住啊,一定要靠理解,記憶只不過是幫助你在考場上偵錯出來的東西,並不是其主導的因素