1. Geometry

在數學中，我們可以用一個方程描述圓：x2+y2=25。這個方程描述的是，一個半徑為5，中心點在（0，0）的圓。這種純數學的描述就是Geometry（幾何）。

但此時，這個「圓」我們是看不見，摸不著的。如果想要看到這個幾何圖形，就必須用畫筆，顏色等資訊，去「繪製」它。

.Net中，Geometry類就是用於描述這種幾何圖形的類。它只包含描述幾何圖形的必要屬性，並提供包括命中測試、動畫等功能。它派生出以下七個類，以簡化對圖形的描述：

1.1 LineGeometry

它表示一條直線。

它主要屬性有EndPoint和StartPoint，用於定義直線的終點和起點。

Point start = new Point(0,0); 
Point end = new Point(50,50); 
LineGeometry line = new LineGeometry(start,end);

1.2 EllipseGeometry

它表示一個橢圓（圓也是橢圓的一種）。

它主要屬性有Center（中心點座標）、RadiusX（x軸半徑）、RadiusY（Y軸半徑）。

Point center = new Point(50,50); 
EllipseGeometry ellipseGeo = new EllipseGeometry(center , 45, 20);

1.3 RectangleGeometry

它表示一個矩形（正方形也是矩形的一種）。

它主要屬性有Rect（矩形框）、RadiusX（x軸半徑）、RadiusY（y軸半徑）。當定義了Rect屬性後，RadiusX和RadiusY的值也就確定了；當給定了RadiusX和RadiusY的值，Rect屬性的值也就確定了。

RectangleGeometry rect = new RectangleGeometry(10,20);

1.4 PathGeometry

它表示一條路線。這條路線中，可以有直線給，也可以有曲線。

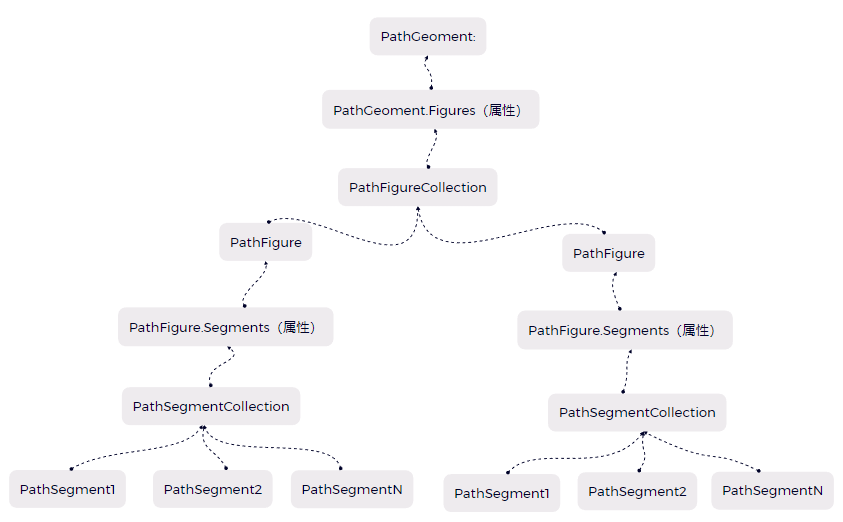
它最重要的屬性是Figures（路徑圖元），型別是PathFigureCollection，意味著它是一個集合，可以裝載多個PathFigure物件。

PathFigure類，有一個重要的屬性Segments，型別是PathSegmentCollection，意味著它也是一個集合，可以裝載多個PathSegment（路徑中的一部分）物件。

由此可見：多個Segment組成了一個PathSegmentCollection（PathFigure的Segment屬性）；多個PathFigure組成了一個PathFigureCollection（PathGeometry的PathFigure屬性）。

// 定義SegmentCollection1 
LineSegment line1 = new(...);                                // 定義直線部分
PolyLineSegment pline1 = new (...)；                         // 定義多段線部分
ArcSegment arc1 = new(...);                                  // 定義弧形線段部分
PathSegmentCollection segments1 = new(new PathSegment[] { line1, pline1, arc1 }); // 定義PathSegment集合 
PathFigure path1 = new(new Point(0, 0), segments1, false);   // 定義第一個的PathFigure 

// 定義SegmentCollection2 
LineSegment line2 = new(...); 
BezierSegment beszier = new(...); // 定義Bezier曲線部分
PathSegmentCollection segments2 = new(new PathSegment[] { line2, beszier }); 
PathFigure path2 = new(new Point(300, 0), segments2, false); // 定義第二個的PathFigure 


// 定義PathFigureCollection 
PathFigureCollection pathFigures = new(new PathFigure[] { path1, path2 }); 
PathGeometry pathGeo = new() { Figures = pathFigures };      // 定義PathGeometry 

 備註：.Net提供「路徑標記語法」用於簡化PathFigures的建立。

1.5 GeometryGroup

它表示多個集合圖形的集合。

它的主要屬性有Children（包含的子圖形），型別是GeometryCollection，意味著它可以可以裝載多個Geometry物件。

LineGeometry lineGeo = new(); 
RectangleGeometry rectGeo = new(); 
PathGeometry pathGeo = new(); 
GeometryGroup geoGroup = new() { Children = new GeometryCollection() { lineGeo, rectGeo, pathGeo } };

GeometryGroup中的幾何圖形，也可以設定FillRule屬性，以設定多個幾何圖形交叉區域的合併方式。

1.6 CombinedGeometry

它表示一個，由兩個幾何圖形組合而成的圖形。

它的主要屬性有Geometry1（幾何圖形1）、Geometry2（幾何圖形2）、GeometryCombineMode（圖形結合的方式）

RectangleGeometry rectGeo = new(); 
PathGeometry pathGeo = new(); 
CombinedGeometry CombineGeo = new(GeometryCombineMode.Exclude, rectGeo, pathGeo);

備註：

• 該類的GeometryCombineMode指的是多個圖形的「結合」方式，這種方式通常指的是布林運算；而部分Geometry物件的FillRule，指的是交疊的圖形的「填充」方式。指的是圖形的重疊閉合區域的「填充」方式；
• 雖然CombineGeometry只能「結合」兩個Geometry物件。但是要注意，Geometry1和Geometry2的型別都是Geometry，意味只要只要是Geometry的子類，都可以賦值給這兩個屬性。因此，可以將多個Geometry填到GemetryGroup中，也可以兩兩CombinedGeometry，然後再將CombinedGeometry再CombinedGeometry。

1.7 StreamGeometry

它是PathGeometry的輕量級表示，不支援資料繫結、動畫或修改。

這意味著，如果PathGeometry佔用太多資源，且不需要資料繫結、動畫、修改等功能，可以用StreamGeometry來替代。

它的工作原理是建立一個StreamGeometryContext物件，並在這個物件中繪製圖形。所以，它沒有圖形資料相關的屬性，

StreamGeometry streamGoe = new(); 
StreamGeometryContext context = streamGoe.Open(); 
context.ArcTo(...); // SteamGeometryContext類提供了多種繪圖方法。 context.PolyLineTo(...); 
context.Close();

 2. Shape

形狀（Shape），就是一個能看得到的幾何圖形。例如我們在白紙上，用紅色的筆畫一條直線，一個矩形。

由此可見，Shape的本質，就是在幾何圖形（Geometry）的基礎上，加上畫筆，顏色等資訊，繪製而成。

.Net中，Shape就是表示「形狀」的類。它是一個抽象類，繼承自FrameworkElement，這意味著它是一個元素，可以直接顯示在表單上。

Shape類派生出了以下幾個類：

這些類都比較容易使用，就不再一一贅述。