CSAPP-Data Lab
gcc -O1 -Wall -m32 -lm -o btest bits.c btest.c decl.c tests.c
In file included from btest.c:16:0:
/usr/include/stdio.h:27:10: fatal error: bits/libc-header-start.h: No such file or directoryinclude <bits/libc-header-start.h>
^~~~~~~~~~~~~~~~~~~~~~~~~~compilation terminated.
In file included from decl.c:1:0:
/usr/include/stdio.h:27:10: fatal error: bits/libc-header-start.h: No such file or directoryinclude <bits/libc-header-start.h>
^~~~~~~~~~~~~~~~~~~~~~~~~~compilation terminated.
In file included from /usr/lib/gcc/x86_64-linux-gnu/7/include-fixed/limits.h:194:0,
from /usr/lib/gcc/x86_64-linux-gnu/7/include-fixed/syslimits.h:7,
from /usr/lib/gcc/x86_64-linux-gnu/7/include-fixed/limits.h:34,
from tests.c:3:
/usr/include/limits.h:26:10: fatal error: bits/libc-header-start.h: No such file or directoryinclude <bits/libc-header-start.h>
^~~~~~~~~~~~~~~~~~~~~~~~~~compilation terminated.
Makefile:11: recipe for target 'btest' failed
make: *** [btest] Error 1
Installed systemd unit for VNC Server in Virtual Mode daemon
Start or stop the service with:
systemctl (start|stop) vncserver-virtuald.service
Mark or unmark the service to be started at boot time with:
systemctl (enable|disable) vncserver-virtuald.service
bitXor
僅使用&和~14步之內完成^
解決思路
通過列舉互斥或(^),按位元與(&)和取反(~)在不同情況下的計算結果可以得到如下結果
^
| 1 | 1 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 |
&
| 1 | 1 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 0 |
~
| 1 | 0 |
| 0 | 1 |
為了描述的方便,設兩數為x和y。通過上述表格不難發現,~(x & y)與(x^y)的結果僅僅在0 0這一種情況下是不正確的,考慮解決這一問題
0 0這種情況運算結果是1,正確結果應當為0,~(~x & ~y)得到的結果恰好可以僅將0 0這種情況結果為0,其他所有情況為1,再&,恰好可以在不變動其他情況的條件下修正0 0的結果
tmin
僅使用! ~ & ^ | + << >>,4步之內獲取最小的32bit的二進位制二補數整數
w位二補數所能表示的範圍為\([-2^{w - 1}, 2^{w - 1} - 1]\)
即1 << 31
isTmax
僅使用 ! ~ & ^ | +,10步之內判斷一個資料是否為最大的32bit的二進位制二補數整數
我的最初想法是
int isTmax(int x) {
return !(~(x + 1) ^ x);
}
我想的是需要用一種方式區分開最大值和其他值
這樣想的理由是隻有在x為最大值時,通過~(x + 1)這種溢位的運算才可以獲取到最大值,然後與x互斥或最大值時為0,再取反得到1
可能這種通過運算溢位的方式不可行
其實回過頭來想,判斷一個數是否為最大值,只需要用最大值和它互斥或即可
我的方式也是想辦法獲得最大值,可是最大值可以直接表示
我忽略了一點,題目不允許使用超過255的資料,所以無法直接使用0x7fffffff,
而且無法使用移位元運算,因此無法構造出最大值
所以只能考慮假設x為最大值,如果操作x構造出最大值
其實上面的做法中通過~(x + 1)是正確得到0x7fffffff的方法
但是答案不正確,是因為-1的存在
換言之, x + 1 = ~x, x == 2147483647 or -1
把這個問題真正解決了可以發現,應該是這麼想,恰好發現2147483647+1的結果與2147483647正好是取反的關係
因此把2147483647+1反過來再與2147483647互斥或恰好可以得到0,這裡其實想的並不是去構造最大值2147483647
而我想的是去構造2147483647,所以沒有關注到這裡會出問題,我實際上找的是x + 1 = -x這樣的x,沒想到除了2147483647,-1也是解,
因此考慮如何區分2147483647和-1,當我看到-1+1的結果是全0後,考慮到這樣一個問題
只有!0=1,其他所有數!結果均不為1,前半部分只有2147483647和-1=0,其他均為1,後半部分只有-1為1,其他均為0
而|會使除-1以外的資料運算結果不變2147483647還是0,其他還是1,而-1會從0變成1,從而就單獨把2147483647區分出來了
這道題如果允許使用移位符其實和下面的allOddBits就是一樣的了
allOddBits
原理:x ^ x = 0
檢測是不是奇數位全為1,只需要構造出奇數位全為1即可,
首先&一下是為了獲得奇數位全為1的形式,如果x不符合條件,那麼&之後的奇數位一定有為0的,^之後的結果就不是0
negate
負數的二補數表示恰好為正數二進位制取反加一
isAsciiDigit
不處在0x30和0x39範圍的條件為
1.前面不是3
2.後面大於9
我在做的時候不會的是如何判斷後面是不是大於9,暴力想法是判斷它是不是10,11,12,13,14,15
但是應當從二進位制的角度去想是不是大於9,大於9只需要首位為1,後面兩位任意一位為1
(x & 0xF0) ^ 0x30錯誤原因在於& 0XF0,當遇到一個位數大於8位元的數位時,從第9位往高位的所有數位都會被0xF0填充的0變成0
因此只要低8位元是0x30,前面不管是多少互斥或的結果都是0
其實0xF0的意圖是想把低4位元清0,以便比較低8位元中的高4位元,但是高位補的0使得結果出現錯誤
如果用我的想法,只要低8位元處在合法範圍內就會將這個數判斷為合法的,原因就是高位的資料被0xF0補充的0所消滅了
conditional
需要根據x的是否為0獲得y或z
通過運算可以得到如下結果
| x | !x | !!x | !!x - 1 | ~(!!x - 1) |
|---|---|---|---|---|
| 不是0 | 00000000000000000000000000000000 | 00000000000000000000000000000001 | 00000000000000000000000000000000 | 11111111111111111111111111111111 |
| 0 | 00000000000000000000000000000001 | 00000000000000000000000000000000 | 11111111111111111111111111111111 | 00000000000000000000000000000000 |
我的想法是首先把x轉化成一個對應的邏輯值0或者1,也就是通過兩次!運算
然後發現如果想取y那麼只需要用全1和它進行&運算,同時用全0與z進行&運算,如果想取z則把這個運算返過來
所以目前的任務是把!!x的結果能夠滿足上述運算的效果,也就是要通過!!x獲得一個全0和全1
但是通過上表可以發現,!!x有兩種結果,而我們必須通過一個相同的操作獲得全0或者全1,可以發現-1恰好可以滿足,而該題不允許使用減號,因此通過加-1實現,而-1的二進位制恰好為對0取反
在解決問題之後,我們回過頭來看這個表格,可以發現,可以不經過!!這個過程,方法是利用資料左移是邏輯移位,右移是算數移動,所謂算數移位是指在向右移動時,左側補充的值是符號位,如果想讓全0還是全0,0000...001變成全1,只需要讓!左移31位元,再右移31位元置,即可以相同的方式實現從!x到!!x-1的轉換
isLessOrEqual
很容易想到判斷x是否小於等於y,只需要判斷x與y的差值是否是小於等於0的即可
x和y的符號有下面幾種可能
| x的符號 | y的符號 | x符號位 | y符號位 |
|---|---|---|---|
| + | + | 0 | 0 |
| + | - | 0 | 1 |
| - | + | 1 | 0 |
| - | - | 1 | 1 |
上面通過減法的結果判斷兩數大小關係是正確的思路,但是在進行減法時,異號之間可能會發生溢位
而異號之間僅通過符號位就可以判斷出大小關係了,不需要進行減法
通過上表可以發現可以區分同號和異號的是符號位互斥或的結果,同號符號位互斥或結果為0,異號符號位互斥或結果為1
而且可以發現,在異號時x是否小於等於y的結果與x的符號位恰好相同
通過上述得到的性質可以使在同號時使用減法來判斷大小關係,在異號時通過符號位判斷大小關係
符號位互斥或的結果就像是一個開關,在一種情況下開啟一個,關閉另一個,另一種情況則正好相反
logicalNeg
這個問題沒有想出來
最初的思路顯然需要找到0和其他資料之間的區別,我認為這道題之所以沒有想出來問題就出在這裡
我的關注點始終放在了一個單獨的資料上,從最終答案來看關注點應當是兩個資料
我想的始終是對於一個非0的資料,怎麼才可以將它與0區分開來,但是始終找不到可行的方法
如果把資料按照數軸列的方式列出來,或許我可以發現相反數的存在
0和-2147483647的相反數是它們本身,其他數的相反數符號位一定與原數符號位相反
通過符號位來進行區分
同時1bit的0和1之間的相互轉化,可以使用!也可以使用^運算
howManyBits
題目中給了幾個Example,看前幾個的時候還是很明確的,但是到了-1就糊塗了,
在二補數中
- 對於正數,預設值都是0,因此最高位的1代表著資料表示的結束
- 對於負數,因為負數的二補數是正數取反得到的,因此預設值為1,因此最高位的0代表著資料表示的結束
因此對於正數,找到最高位1所在位數+1即為答案,對於負數,找到最高位0所在位數+1即為答案
顯然-1對應的答案也是滿足上述方法的,只是確實不太好理解,因為它只留下了一個符號位,既是符號位同時轉為原碼後也能代表+1
正數和負數的尋找目標是不同的,但是可以對負數按位元取反,從而將正負數的操作統一為尋找最高位的1
到此為止,還是通過思考可以想出來的,後續的問題就是如何得到最高位1所在的位數
單就統計位數這個問題我就沒有相出什麼辦法,沒想出來怎麼可以實現計數
方法是看看高16位元是否存在1,如果存在,那麼位數計數要從16開始(這個可以通過移位實現)
之後把原來的資料變成原來的高16位元或低16位元,這取決於高16位元是否存在1
之後看高8位元,按照相同的過程直到變成看高1位從而找到1
判斷一個數中有沒有1等價於看這個數是否為0,通過!運算即可實現
!!(x >> 16):x的高16位元是否存在1 - 存在1,那麼接下來的尋找空間就由原來的32bit變為高16bit,因此需要把x右移16位元,而答案位數最低也是16了,因此還要對答案累積16,因此可以發現x要移動的位數和答案要累積的數值是相等的,所以直接對
!!(x >> 16)進行移位 - 不存在1,尋找空間由原來的32bit變為低16bit,x需要右移0位,答案位數最低為0
上述兩種情況都按照存在1的方式進行移位均可以得到正確結果
如果!!(x >> 16)為1代表最高位1存在於高16位元,假設最高位1位於17bit,那麼此時bit_16的結果代表最高位1的後面一位
bit_1代表在2位中最高位1是否存在於高1位,把bit_16到bit_1的結果相加得到的應當是最高位1所在位置的下一位,比如最高位1處在4,那麼bit_16到bit_1的和就是3,處在4的下一位
而我們的目標是最高位的1所處的位置,而非最高位1的下一位所處的位置
因此還需要加上最高位1本身,但是這裡不能直接+1,如果存在最高位1,直接加1確實可以,但是如果不存在最高1應當加0
所以一個等效的辦法是加上最後處理完成後的僅剩1位的x,x如果是1代表存在最高位1,那麼加1,即加上它本身的位置,x如果為,說明不存在最高位1,加上0答案也是正確的
float_twice

-
exp不為全0或全1,全0和全1有特殊用途
-
階碼E=exp-bias(偏置值),exp是無符號資料的值,bias有計算公式\(2^{k - 1} - 1\),在單精度浮點數中=127
-
尾數M存在規格化的問題,表示為1.xxx的形式,把原數中的小數點左移,通過階碼來表示這種移動
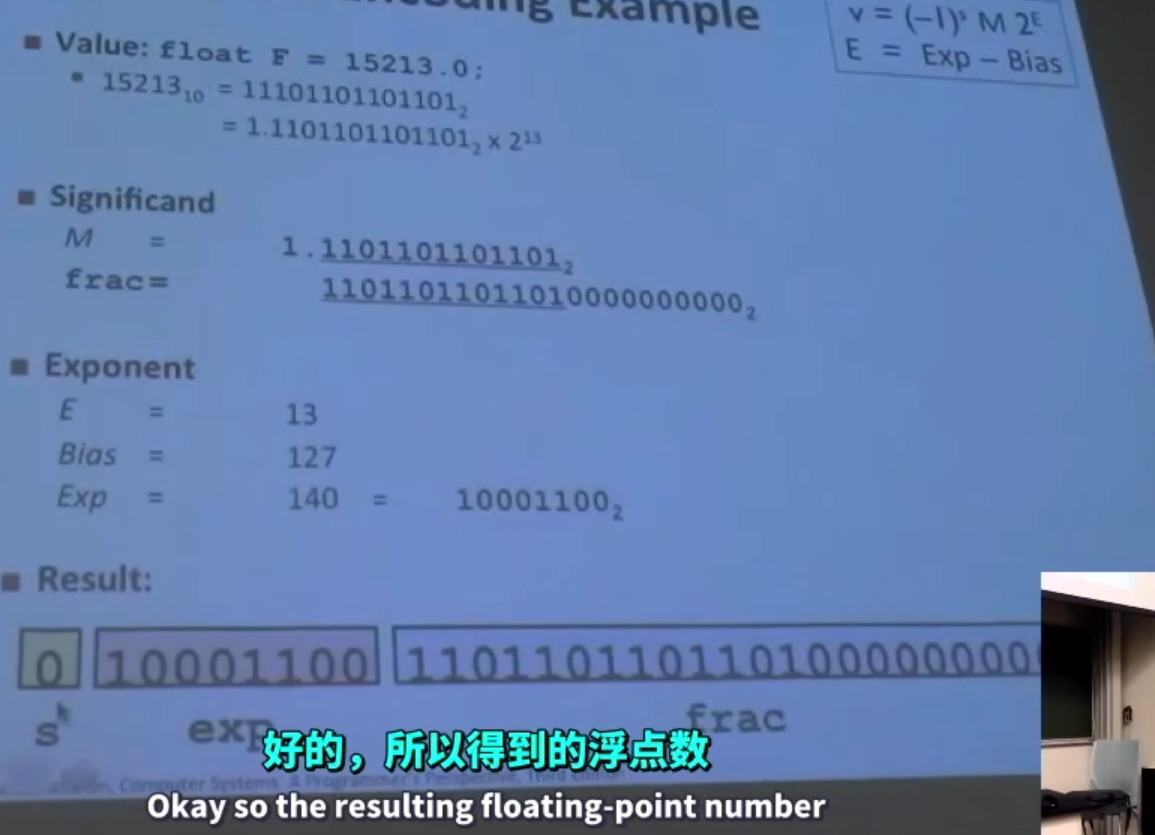
frac之所以向右側補0,是因為frac表示的是小數點右側的數值,是從左側開始計數的,因此向右側補0,就像小數點左側是從右側開始計數,向左側補0
單精度格式分類

以下公式的立足點在於已知上圖中的資料推匯出原數,即從exp和f推匯出E和M
-
規格化
\(E = exp - Bias(exp = E + Bias)\)
\(M = 1 + f(M = 1.f_{n - 1}f_{n - 2}...f_{0})\),所以f實際是將M小數點移到左側最高位之後的位置,小數點右側的內容
-
非規格化
非規格化數的用途是:1.表示0; 2.表示非常接近0的數
階碼域為全0時,即\(exp=0\)時
如果按照規格化的規定,應當有\(E = 0 - Bias = -Bias\),但是卻規定\(E = 1 - Bias\)
M = f, 即f表示的小數是多少M就是多少,與規格化的區別在於缺少了隱含的開頭的1
-
無窮大
exp為全1,frac為全0,s為0時代表正無窮,s為1時代表負無窮
-
NaN
exp為全1,frac不為0時,表示不能是實數和無窮的數值
解題
對於給定的一個資料,存在以下幾種情況
-
規格化數
exp+1即可,但要考慮是否會發生溢位
如果結果變為全1,是不是要返回無窮,沒道理變成Nan,變成無窮是不是還要把frac變成全0。答案是對的,規格化數的最大值的exp加1後應當變為無窮,確實要把frac修改為全0
exp為全0
-
非規格化數
感覺上是對frac直接乘2,如果超過非規格化範圍怎麼辦?
*2就是對frac直接左移1位,如果超過了非規格化的範圍,最左側的1會移動到exp的範圍內,很神奇的是此時不需要進行任何操作結果恰好是正確的,這裡可能和非規格化標準的定義有關係
exp為全1
-
無窮大和無窮小
直接返回原數即可
-
NaN
直接返回Nan即可
需要注意的是這裡沒有僅能使用8bit資料的限制了,可以使用32bit的資料了,所以提取資料就變得簡單許多
問題是把unsigned uf的uf的二進位制直接當作浮點數了,不是說給定一個值要先轉化為二進位制然後再根據E和exp,f和M的關係轉換為浮點數,而是它的二進位制本身就是浮點數,這點我一直理解的有問題。因為題目中採用的是無符號數,而且把這個無符號數就當作了浮點數,所以在給定一個資料時它的二進位制表現形式就直接被當作浮點數了,所以這也就是為什麼2147483647是NaN了,因為它的二進位制表現形式是0x7fffffff,對應exp位置的是0xff,對應frac位置的又不為0,剛好是浮點數中NaN的表現形式
float_i2f
作為引數的int可能是一個負數,但是在修改為float形式時,都是觀察正數的情況的,之後修改符號位為1
把int轉化為float,採用unsigned形式儲存並返回
浮點數包含以下幾種情況:
-
規格化
-
非規格化
-
無窮
-
NaN
int的表示範圍為[-2147483648, 2147483647]
這個範圍內的數轉化為float時,不會出現2(0除外),3,4的情況
所以要處理的只是0和規格化數
由於不存在NaN和無窮的情況,所以exp還是很好處理的
難點在於frac的處理,一方面要考慮尾數不夠23bit和超過23bit兩種情況
不夠23bit向左移,右側自動補0不會出什麼問題
如果超過23bit需要向右移,這時候出現一個問題是右側被丟棄的位涉及到資料的舍入,IEEE預設的舍入的規則為向偶數舍入,通俗地說可以為4舍6入5取偶數,不夠一半就捨棄,例如1.4->1,超過1半就升上去,例如1.6->2,剛好一半就向最接近的偶數靠近,例如1.5->2,2.5->2,對於3.5這種減少和增加都可以到達偶數的,預設升上去變為4
上面是以10進位製為例的,2進位制的規則見下方例子
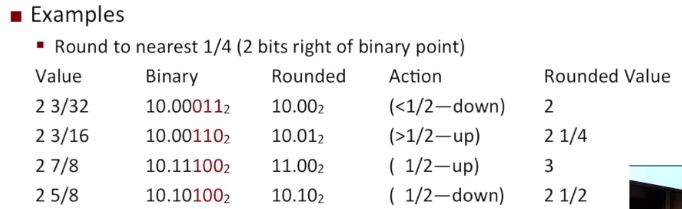
相當於保留精度到整數
-
xxx.0xxxx: 直接捨棄小數部分,不需要進行操作
-
xxx.10000 (對應
else flag = frac & 1)- xx1.100000: 升上去 (flag = 1)
- xx0.100000: 已經是偶數不需要處理的 (flag = 0)
-
xxx.10001: 升上去 (對應
if (m & 1) flag = 1)
float_f2i

int轉float時,由於int本身的限制,轉float時並不會出現非規格化,無窮和NaN的資料
但是float轉int時,由於float本身那幾種形式都有可能出現,所以分開討論
-
規格化
exp不為全0和全1
-
非規格化
exp為全0,結果是0(此處其實還有疑惑,為何浮點數向整形轉換會直接捨棄掉小數部分?例如浮點數0.9轉換為int時直接變為0)
-
無窮
exp為全1,frac為全0,返回題目規定值
-
NaN
exp為全1,frac不為全0,返回題目規定值
容易被忽視的一點是,在規格化時,當exp計算得出的e過大使得表示的資料超出int的範圍時應當返回題目規定值,所以這也就涉及到了如何判斷是否溢位
int的最大值是01111111111111111111111111111111,即\(1.1...1 * 2^{30}\),所以我覺得當超過30時即會超出範圍(此處還有疑問,超過30即\(>= 31\),但實際測試設定為\(> 31\)結果依然正確,嘗試將溢位的範圍設定更大時依然可以得到正確結果,嘗試檢視測試資料,但是沒有找到),巧合的是當浮點數為無窮和NaN時的e也是超出這個範圍的,所以可以將操作進行合併
首先計算e,根據e即可區分幾種情況