1.二元樹的遍歷

二元樹主要有兩種遍歷方式：

深度優先遍歷：先往深走，遇到葉子節點再往回走。

前序遍歷（遞迴法，迭代法）中左右
中序遍歷（遞迴法，迭代法）左中右
後序遍歷（遞迴法，迭代法）左右中

廣度優先遍歷：一層一層的去遍歷。

層次遍歷（迭代法）

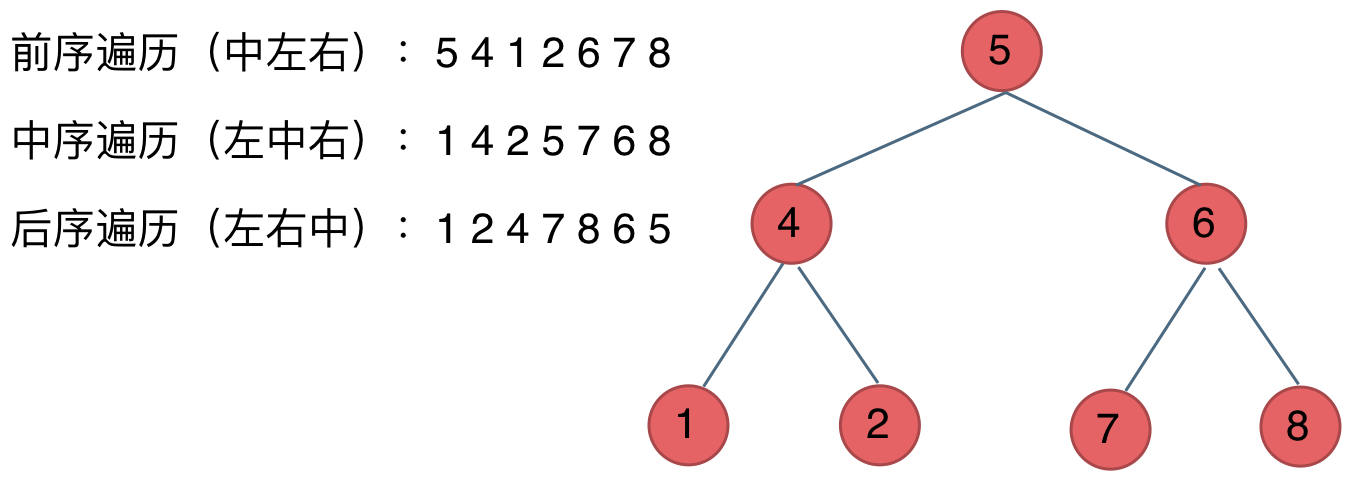
對比圖可以理解一下遍歷的過程，前中後序遍歷涉及遞迴和迭代兩種方法講解。

2.LeetCode連結

前序遍歷：https://leetcode.cn/problems/binary-tree-preorder-traversal/submissions/

中序遍歷：https://leetcode.cn/problems/binary-tree-inorder-traversal/submissions/

後序遍歷：https://leetcode.cn/problems/binary-tree-postorder-traversal/submissions/

層序遍歷：https://leetcode.cn/problems/binary-tree-level-order-traversal/submissions/

感興趣的可以去練練手！！！

3.前序遍歷

前序遍歷的順序是中左右，即先根節點、左子樹、右子樹，那麼我們先考慮遞迴進行求解。

要列印出前序遍歷節點的數值，所以引數裡需要放節點的數值，除了這一點就不需要在處理什麼資料了也不需要有返回值，所以遞迴函數返回型別就是void。

　　 Traversal(TreeNode root, List<Integer> list)

當前遍歷的節點是空了，那麼本層遞迴就要要結束了，所以如果當前遍歷的這個節點是空，就直接return。

if (cur == NULL) return;

前序遍歷是中左右的循序，所以在單層遞迴的邏輯，是要先取中節點的數值。

list.add(root.val);

Traversal(root.left, list);

Traversal(root.right, list);

所以總體的遞迴程式碼如下：

class Solution {
    public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> result = new ArrayList<Integer>();
        preorder(root, result);
        return result;
    }

    public void preorder(TreeNode root, List<Integer> result) {
        if (root == null) {
            return;
        }
        result.add(root.val);
        preorder(root.left, result);
        preorder(root.right, result);
    }
}

對於迭代法，難度會更大一點！！！

前序遍歷是中左右，每次先處理的是中間節點，那麼先將根節點放入棧中，然後將右孩子加入棧，再加入左孩子。為什麼要先加入右孩子，再加入左孩子呢？因為這樣出棧的時候才是中左右的順序。

所以我們不難寫出程式碼如下：

class Solution {
    public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> result = new ArrayList<>();
        if (root == null){
            return result;
        }
        Stack<TreeNode> stack = new Stack<>();
        stack.push(root);
        while (!stack.isEmpty()){
            TreeNode node = stack.pop();
            result.add(node.val);
            if (node.right != null){
                stack.push(node.right);
            }
            if (node.left != null){
                stack.push(node.left);
            }
        }
        return result;
    }
}

4.中序遍歷

中序遍歷的順序是左中右，即先左子樹、根節點、右子樹，那麼我們先考慮遞迴進行求解。

　　思路和上面一樣，唯一的區別就是變了順序，所以總體的遞迴程式碼如下：

class Solution {
    public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> result = new ArrayList<Integer>();
        preorder(root, result);
        return result;
    }

    public void preorder(TreeNode root, List<Integer> result) {
        if (root == null) {
            return;
        }
        preorder(root.left, result);
        result.add(root.val);   //注意
        preorder(root.right, result);
    }
}

　　對於迭代法，難度會更大一點！！！

　　中序遍歷是左中右，但是程式碼和上面有一些不同，中序遍歷是左中右，先存取的是二元樹頂部的節點，然後一層一層向下存取，直到到達樹左面的最底部，再開始處理節點（也就是在把節點的數值放進result陣列中），這就造成了處理順序和存取順序是不一致的。在使用迭代法寫中序遍歷，就需要借用指標的遍歷來幫助存取節點，棧則用來處理節點上的元素。

　　所以我們可以寫出程式碼如下：

class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> result = new ArrayList<>();
        if (root == null){
            return result;
        }
        Stack<TreeNode> stack = new Stack<>();
        TreeNode cur = root;
        while (cur != null || !stack.isEmpty()){
           if (cur != null){
               stack.push(cur);
               cur = cur.left;
           }else{
               cur = stack.pop();
               result.add(cur.val);
               cur = cur.right;
           }
        }
        return result;
    }
}

5.後序遍歷

　　後序遍歷的順序是左右中，即先左子樹、右子樹、根節點，那麼我們先考慮遞迴進行求解。

　　思路和上面一樣，唯一的區別就是變了順序，所以總體的遞迴程式碼如下：

class Solution {
    public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> result = new ArrayList<Integer>();
        preorder(root, result);
        return result;
    }

    public void preorder(TreeNode root, List<Integer> result) {
        if (root == null) {
            return;
        }
        preorder(root.left, result);
        preorder(root.right, result);
        result.add(root.val);   //注意
    }
}

　　對於迭代法，會前序遍歷難度會小一點！！！

　　先序遍歷是中左右，後續遍歷是左右中，那麼我們只需要調整一下先序遍歷的程式碼順序，就變成中右左的遍歷順序，然後在反轉result陣列，輸出的結果順序就是左右中了，如下圖：

　　所以我們可以很快的寫出程式碼如下：

class Solution {
    public List<Integer> postorderTraversal(TreeNode root) {
        List<Integer> result = new ArrayList<>();
        if (root == null){
            return result;
        }
        Stack<TreeNode> stack = new Stack<>();
        stack.push(root);
        while (!stack.isEmpty()){
            TreeNode node = stack.pop();
            result.add(node.val);
            if (node.left != null){
                stack.push(node.left);
            }
            if (node.right != null){
                stack.push(node.right);
            }
        }
        Collections.reverse(result);
        return result;
    }
}

　　注意，這裡主要是入棧順序變了，變成先左後右！！！

6.層序遍歷

層序遍歷一個二元樹。就是從左到右一層一層的去遍歷二元樹。這種遍歷的方式和我們之前講過的都不太一樣。

需要借用一個輔助資料結構即佇列來實現，佇列先進先出，符合一層一層遍歷的邏輯，而是用棧先進後出適合模擬深度優先遍歷也就是遞迴的邏輯。

瞭解了思路，我們可以很快的寫出層序遍歷的程式碼：

class Solution {
    public List<List<Integer>> resList = new ArrayList<List<Integer>>();
    public List<List<Integer>> levelOrder(TreeNode root) {
        checkFun02(root);
        return resList;
    }
    public void checkFun02(TreeNode node) {
        if (node == null) return;
        Queue<TreeNode> que = new LinkedList<TreeNode>();
        que.offer(node);
        while (!que.isEmpty()) {
            List<Integer> itemList = new ArrayList<Integer>();
            int len = que.size();
            while (len > 0) {
                TreeNode tmpNode = que.poll();
                itemList.add(tmpNode.val);
                if (tmpNode.left != null) que.offer(tmpNode.left);
                if (tmpNode.right != null) que.offer(tmpNode.right);
                len--;
            }
            resList.add(itemList);
        }
    }
}

　　主要就是建立一個佇列，依次對出佇列的數的左右子樹入隊，同時記錄下當前佇列的大小，這樣可以每一次得到一層的數。

　　怎麼樣，看完以後是不是簡單多了，當然得有一點點這個方面基礎，不然看起來還是有點費勁！！！