非自交任意多邊形與矩形框的交集面積計算方法

1、應用背景

  在物件識別的AI計算時，有時需要限定檢測區域，即目標物件落在限定區域內有效，在區域外忽略。
  轉換為數學模型為：目標檢測框與限定區域（非自交多邊形）的交集面積除以目標檢測框面積（類似於IOU值），超過門限（如50%），判定為在限定區域內。
  整個問題歸結為計算目標檢測框與限定區域的交集面積。
  多邊形用頂點列表表示：點集P={pi|i=0,1,...,n-1}，為順序的n個點，n>=3，則多邊形為：p0->p1->...->pn-1->p0。對於點p(i)，p(i-1)表示前一個點，p(i+1)表示後一個點。本文下面涉及到p(i)，如果i小於0，則i=(i+n) % n。
  約定輸入多邊形為非自交的，所謂自交，如ABCD是正常矩形，則ABDC就是自交的。
  限定區域，可以表示為多個多邊形的列表（本演演算法要求限定區域的多邊形之間的交集為空，否則需要計算凸多邊形之間的交集）。

2、演演算法步驟

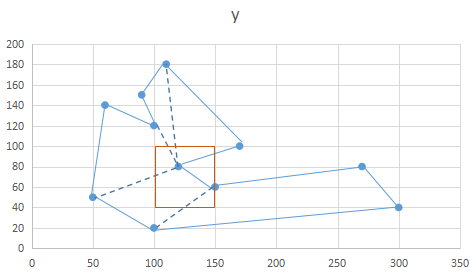
2.1、先計算多邊形的方向，是順時針，還是逆時針。

  影象座標，X軸方向從左到右，Y軸方向從上到下。順時針為1，逆時針為-1。
  搜尋多變形最左側點，如果最左側點有多個，取左側最下面的點。不妨設該點為p1，對應下標為k，計算點p的叉乘。p0表示p1的前一點，p2表示p1的後一點。
  即向量p0p1與向量p1p2的叉乘：cross_product = (p1.x-p0.x)(p2.y-p1.y) - (p1.y-p0.y)(p2.x-p1.x)
  如果cross_product>0，為順時針；cross_product<0，則逆時針；cross_product=0，為平行線，即p0,p1,p2三點共線，但p1的取法已確保三點不共線，除非多邊形所有點都在一垂直線上，這種情況可以報錯處理。
  這樣得到的多邊形的方向：clockwise值：順時針為1，逆時針為-1。

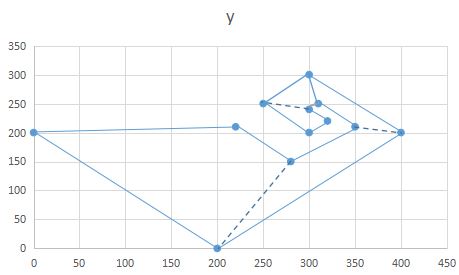
2.2、處理凹多邊形

  檢測多邊形的凸性，如果為凹多邊形，則切分為多個凸多邊形；如果為凸多邊形，則返回。
  對於多邊形P，逐點計算叉乘，如果cross_product*clockwise 小於等於 0，則認為是凹點，表示多邊形為凹多邊形。
  針對第一個凹點p(i)，從p(i-2)開始反向掃描，檢測向量p(i-1)p(i)與向量p(i)p(k)的叉乘，k=i-2,...0,1,..i+1-n，取得反向掃描的第一個凹點p(c-1)的之後一點p(c)，即表示最大的凸多邊形。切分p(c),...p(i)為新的多邊形P1，p(i)p(c)連線為切分線，p(i)、p(c)及餘下的點組成剩餘多邊形P2。
  對於切分得到的多邊形P1和P2，遞迴使用本演演算法，直到所有多邊形都是凸多邊形。
  演演算法的效果圖如下：

2.3、計算所有凸多邊形的外接矩形

  針對已得到的凸多邊形列表，逐個計算外接矩形。得到外接矩形列表：outBoundRectangeList。外接矩形與凸多邊形一一對應。
  使用外接矩形，可以簡化後續處理。

2.4、計算外接矩形與目標檢測框的交集

  目標檢測框為矩形，外接矩形與目標檢測框的交集，結果為矩形或空集。如果為空集，表示凸多邊形與目標檢測框無交，如果交集非空，則進入下一步處理。

2.5、計算交集矩形與凸多邊形的交集多邊形

  以交集矩形的4條邊線所在直線，分別計算直線與凸多邊形的交點，按上邊線、右邊線、下邊線、左邊線次序。根據交集矩形的生成方法，各邊線與凸多邊形必然都有交點，如果交點為多邊形頂點，則進一步判斷頂點的2條邊的鄰接點是否在邊線的同一側，如果為同一側，則該頂點算兩個點。如果2個鄰接點在邊線的兩側或有一邊在邊線上，則計為一個點。這樣，每條邊線與凸多邊形的交點都是兩個。
  對於上邊的兩個交點，y軸的值為rcy1,設x軸的值分別為x1和x2，交集矩形的上邊端點x軸值為rcx1和rcx2，則上邊線段的交集線段：
  v1=max(rcx1,min(x1,x2))
  v2=min(rcx2,max(x1,x2))
  如果v1>v2，表示線段無交集；如果v1==v2，表示一個交點；如果v1小於v2，則交集上邊線段端點(v1,​rxy1)和(v2,​rxy1)。將交點加入交集多邊形中，新增順序，按順時針次序方向加入，無交集則不加。
  類似方法處理右邊線，下邊線，左邊線。
  最後得到：交集矩形與凸多邊形的交集多邊形，可能的形狀如下：

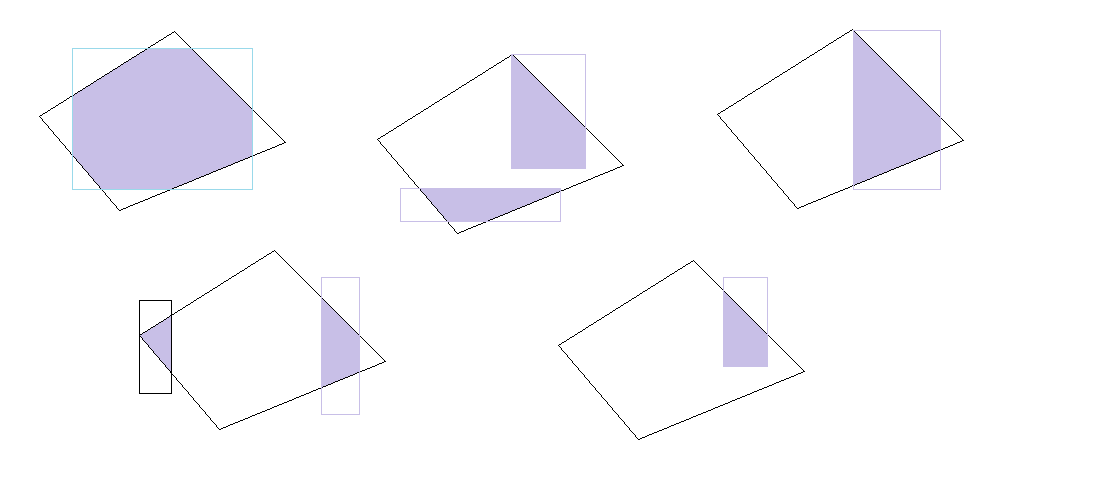
2.6、計算交集多邊形面積

  交集多邊形為凸多邊形，因此面積計算可使用三角形方法，以p0點為固定點，依次取p(i-1)和p(i),i=2,..,n-1，得到三角形列表。
  三角形的面積計算，假設三點分別為p1=(x1,y1),p2=(x2,y2),p3=(x3,y3)，則三角形面積為:
  S=(x1y2-x2y1+x3y1-x1y3+x2y3-x3y2)/2=[x1(y2-y3)-x2(y1-y3)+x3(y1-y2)]/2，這個公式可使用行列式表示：

  利用三角形座標計算面積的公式推導如下：
  如下圖的三角形：

  三角形面積等於外接矩形框面積減去三個著色的三角形面積，影象座標Y軸從上到下，即：
  S=(x2-x3)(y3-y1)-((x2-x1)(y2-y1)+(x2-x3)(y3-y2)+(x1-x3)(y3-y1))/2
  整理後，即可得到之前的三角形面積公式。
  累加交集多邊形的所有三角形的面積，得到一個交集多邊形的面積。

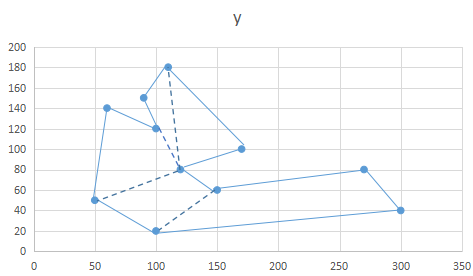
2.7、計算凸多邊形與目標檢測框的交集多邊形面積

  累加所有凸多邊形與目標檢測框的交集多邊形面積。效果圖如下：