基於PHP實現堆排序原理

堆

堆(heap)是電腦科學中一類特殊的資料結構的統稱，通常是一個可以被看做一棵樹的陣列物件。

堆{k1,k2,ki,…,kn} (ki <= k2i,ki <= k2i+1)|(ki >= k2i,ki >= k2i+1), (i = 1,2,3,4...n/2)

關於堆：

• 堆中某個節點的值總是不大於或不小於其父節點的值；
• 堆總是一棵完全二元樹（下面）。
• 將根節點最大的堆叫做最大堆或大根堆，根節點最小的堆叫做最小堆或小根堆。

完全二元樹

說到堆排序，就不能不提完全二元樹，這些基本概念在網上到處都是，我摘了個最簡單的。。

完全二元樹：除最後一層外，每一層上的節點數均達到最大值；在最後一層上只缺少右邊的若干結點。

我自己總結認為，正是因為有下面兩個特點，

• 只允許最後一層有空缺結點且空缺在右邊，即葉子結點只能在層次最大的兩層上出現（儲存方式的規則性）；
• 若i>1，tree的雙親為tree[i p 2]（其父子結點值的規律性）；

才使得其進行排序非常方便。

堆排序

堆排序求升序用大頂堆，求降序用小頂堆。

本例用求降序的小頂堆來解析。

堆排序步驟如下：

1、我們將資料（49、38、65、97、76、13、27、50）建立一個陣列$arr；

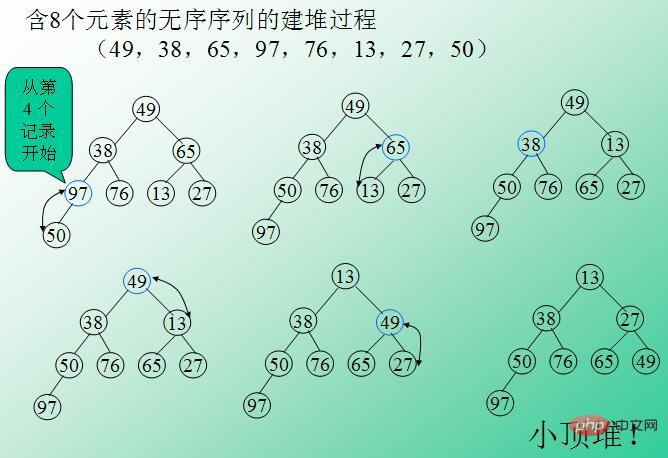
2、用陣列$arr建立一個小頂堆（主要步驟，會在程式碼注釋裡解釋，下圖是用一個陣列建立小頂堆的過程）；

3、將堆的根（最小的元素）與最後一個葉子交換，並將堆長度減一，跳到第二步；

4、重複2-3步，直到堆中只有一個結點，排序完成。

堆排序的PHP實現

//因為是陣列,下標從0開始,所以,下標為n根結點的左子結點為2n+1,右子結點為2n+2; 
//初始化值,建立初始堆
$arr=array(49,38,65,97,76,13,27,50);
$arrSize=count($arr);

//將第一次排序抽出來，因為最後一次排序不需要再交換值了。
buildHeap($arr,$arrSize);

for($i=$arrSize-1;$i>0;$i--){
  swap($arr,$i,0);
  $arrSize--;
  buildHeap($arr,$arrSize);  
}

//用陣列建立最小堆
function buildHeap(&$arr,$arrSize){
  //計算出最開始的下標$index,如圖,為數位"97"所在位置,比較每一個子樹的父結點和子結點,將最小值存入父結點中
  //從$index處對一個樹進行迴圈比較,形成最小堆
  for($index=intval($arrSize/2)-1; $index>=0; $index--){
    //如果有左節點,將其下標存進最小值$min
    if($index*2+1<$arrSize){
      $min=$index*2+1;
      //如果有右子結點,比較左右結點的大小,如果右子結點更小,將其結點的下標記錄進最小值$min
      if($index*2+2<$arrSize){
        if($arr[$index*2+2]<$arr[$min]){
          $min=$index*2+2;
        }
      }
      //將子結點中較小的和父結點比較,若子結點較小,與父結點交換位置,同時更新較小
      if($arr[$min]<$arr[$index]){
        swap($arr,$min,$index);
      }  
    }
  }
}

//此函數用來交換下陣列$arr中下標為$one和$another的資料
function swap(&$arr,$one,$another){
  $tmp=$arr[$one];
  $arr[$one]=$arr[$another];
  $arr[$another]=$tmp;
}

下面是排序的最終結果：

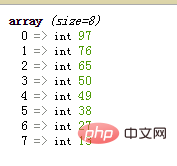
堆用來進行全排序，時間複雜度是O(nlogn)

而快排用來全排序，平均時間複雜度也是O(nlogn)

但堆排序可以用來求 TopK 時，堆的時間複雜度為O(Klog2(n)，因為它只需要進行 K 輪排序即可。

推薦教學：《PHP》

以上就是基於PHP實現堆排序原理的詳細內容，更多請關注TW511.COM其它相關文章！