技術文章 » 強化學習-學習筆記6 | 蒙特卡洛演演算法

強化學習-學習筆記6 | 蒙特卡洛演演算法

2022-07-06 21:00:49

Monte Carlo Algorithms. 蒙特卡洛演演算法是一大類隨機演演算法，又稱為隨機抽樣或統計試驗方法，通過隨機樣本估計真實值。

下面用幾個範例來理解蒙特卡洛演演算法。

6. 蒙特卡洛演演算法

6.1 計算 \(\pi\)

a. 原理

如果我們不知道 \(\pi\) 的值，我們能不能用亂數 來近似 \(\pi\) 呢？

假設我們用一個亂數生成器，每次生成兩個範圍在 \([-1,+1]\) 的亂數，一個作為 x，另一個作為 y，即生成了一個二維隨機點：

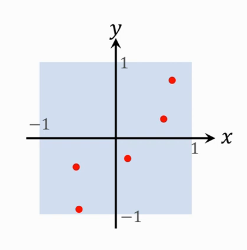
假如生成 1億 個隨機樣本，會有多少落在 半徑=1 的圓內？這個概率就是圓的面積除以正方形的面積。

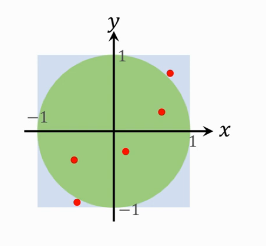
即：\(P = \frac{\pi{r^2}}{2^2}=\frac{\pi}{4}\)

假設從正方形區域中隨機抽樣 n 個點，那麼落在圓內點個數的期望為：\(P_n=\frac{\pi{n}}{4}\)，

下面我們去求落在圓內的點的個數，只需滿足\(x^2+y^2\leqslant1\) 即為圓內。

如果生成的隨機點的個數足夠多，落在圓內的實際觀測值 \(m\approx \frac{\pi{n}}{4}\)；

我們已知了m 與 n，所以\(\pi \approx \frac{4m}{n}\).

事實上，根據概率論大數定律：

\(\frac{4m}{n}\rightarrow \pi\)，as n → ∞

這保證了蒙特卡洛的正確性。

伯恩斯坦概率不等式還能確定 觀測值和真實值之間誤差的上界。

\(|\frac{4m}{n}-\pi|=O(\frac{1}{\sqrt{n}})\)

說明 這個誤差與樣本n的根號成反比。

b. 程式碼

下面放一個Python程式碼

#coding=utf-8
#蒙特卡羅方法計算 pi
import random,math,time
start_time = time.perf_counter()
s = 1000*1000
hits = 0
for i in range(s):
    x = random.random()
    y = random.random()
    z = math.sqrt(x**2+y**2)
    if z<=1:
        hits +=1

PI = 4*(hits/s)
print(PI)
end_time = time.perf_counter()
print("{:.2f}S".format(end_time-start_time))

# 輸出
3.141212
0.89S

另外可還有一個視覺化程式，可以模擬點落在方塊區域圓內外：http://www.anders.wang/monte-carlo/

6.2 Buffon's Needle Problem

a. 原理

布封投針，也是用蒙特卡洛來近似 \(\pi\) 值。這是一個可以動手做的實驗。

用一張紙，畫若干等距平行線（距離為 d），撒上一把等長的針（長度為l），通過與平行線相交的針的數量，就可以推算出 \(\pi\)。

通過微積分可以算出：相交的概率為：\(P = \frac{2l}{\pi{d}}\)

微積分推導過程：

課程裡並沒有講解推導，這裡我參考的是一下兩篇部落格的推導過程：

  1. https://zhuanlan.zhihu.com/p/479953215
  2. https://cosx.org/2009/11/a-brief-talk-on-buffon-throwing-needle-problems/

主流做法是通過對針的斜率進行積分：

這裡我後續補充。

跟 6.1 類似，我們隨機扔 n 根針，這樣相交個數的期望為 \(Pn = \frac{2ln}{\pi{d}}\) 。我們可以觀察到（如果是電腦模擬即為通過公式判斷出）有 m 跟針實際與線相交，如果n足夠大，則 \(m\approx \frac{2ln}{\pi{d}}\)。

求 \(\pi\) 公式即為： \(\pi\approx \frac{2ln}{md}\)

b. 程式碼

有了公式 \(\pi\approx \frac{2ln}{md}\)，程式碼實現其實很簡單了，僅列出一種實現思路：

import numpy as np

def buffon(a,l,n):
  xl = np.pi*np.random.random(n)
  yl = 0.5*a*np.random.random(n)
  m = 0
  for x,y in zip(xl,yl):
    if y < 0.5*l*np.sin(x):
      m+=1
  result = 2*l/a*n/m
  print(f'pi的估計值是{result}')
  
buffon(2,1,1000000)

# 輸出為：
pi的估計值是3.153977165205324

當然，也有視覺化的程式碼：

import matplotlib.pyplot as plt
import random
import math
import numpy as np

NUMBER_OF_NEEDLES = 5000


class DefineNeedle:
    def __init__(self, x=None, y=None, theta=None, length=0.5):
        if x is None:
            x = random.uniform(0, 1)
        if y is None:
            y = random.uniform(0, 1)
        if theta is None:
            theta = random.uniform(0, math.pi)

        self.needle_coordinates = np.array([x, y])
        self.complex_representation = np.array(
            [length/2 * math.cos(theta), length/2*math.sin(theta)])
        self.end_points = np.array([np.add(self.needle_coordinates, -1*np.array(
            self.complex_representation)), np.add(self.needle_coordinates, self.complex_representation)])

    def intersects_with_y(self, y):
        return self.end_points[0][1] < y and self.end_points[1][1] > y


class BuffonSimulation:
    def __init__(self):
        self.floor = []
        self.boards = 2
        self.list_of_needle_objects = []
        self.number_of_intersections = 0

        fig = plt.figure(figsize=(10, 10))
        self.buffon = plt.subplot()
        self.results_text = fig.text(
            0, 0, self.estimate_pi(), size=15)
        self.buffon.set_xlim(-0.1, 1.1)
        self.buffon.set_ylim(-0.1, 1.1)

    def plot_floor_boards(self):
        for j in range(self.boards):
            self.floor.append(0+j)
            self.buffon.hlines(
                y=self.floor[j], xmin=0, xmax=1, color='black', linestyle='--', linewidth=2.0)

    def toss_needles(self):
        needle_object = DefineNeedle()
        self.list_of_needle_objects.append(needle_object)
        x_coordinates = [needle_object.end_points[0]
                         [0], needle_object.end_points[1][0]]
        y_coordinates = [needle_object.end_points[0]
                         [1], needle_object.end_points[1][1]]

        for board in range(self.boards):
            if needle_object.intersects_with_y(self.floor[board]):
                self.number_of_intersections += 1
                self.buffon.plot(x_coordinates, y_coordinates,
                                 color='green', linewidth=1)
                return
        self.buffon.plot(x_coordinates, y_coordinates,
                         color='red', linewidth=1)

    def estimate_pi(self, needles_tossed=0):
        if self.number_of_intersections == 0:
            estimated_pi = 0
        else:
            estimated_pi = (needles_tossed) / \
                (1 * self.number_of_intersections)
        error = abs(((math.pi - estimated_pi)/math.pi)*100)
        return (" Intersections:" + str(self.number_of_intersections) +
                "\n Total Needles: " + str(needles_tossed) +
                "\n Approximation of Pi: " + str(estimated_pi) +
                "\n Error: " + str(error) + "%")

    def plot_needles(self):
        for needle in range(NUMBER_OF_NEEDLES):
            self.toss_needles()
            self.results_text.set_text(self.estimate_pi(needle+1))
            if (needle+1) % 200 == 0:
                plt.pause(1/200)
        plt.title("Estimation of Pi using Probability")

    def plot(self):
        self.plot_floor_boards()
        self.plot_needles()
        plt.show()


simulation = BuffonSimulation()
simulation.plot()

效果如圖：

以上內容參考：

  1. 課程視訊
  2. https://www.section.io/engineering-education/buffon-needle/
  3. https://github.com/topics/buffon-needle
  4. https://github.com/GunnarDahm/buffon_monte_carlo_sim/blob/master/buffon_monte_carlo.py
  5. https://blog.csdn.net/qq_45757739/article/details/108387567
  6. https://blog.csdn.net/TSzero/article/details/111604960

理解思想即可，如果後續有機會，可能單出一篇介紹介紹，也有可能將這部分豐富一下。

6.3 估計陰影部分的面積

我們稍微推廣一下，試著用蒙特卡洛解決一個陰影部分面積的求解。比如下圖：

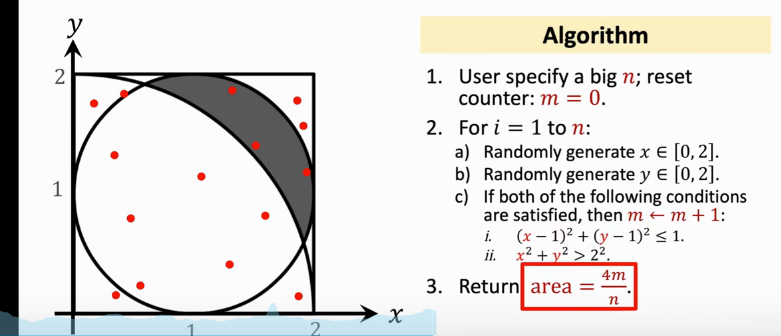
我們如何使用蒙特卡洛的思路解決這個陰影部分面積的求解呢？

類似於上面的思路，在正方形內做隨機均勻抽樣，得到很多點，怎麼確定點在陰影部分呢？

可知，陰影部分的點滿足：

\[\begin{cases} x^2+y^2>4\\ (x-1)^2+(y-1)^2\leq1\end{cases} \]

  • 易知，正方形面積 \(A_1=4\)；設陰影部分面積為 \(A_2\)
  • 隨機抽樣的點落在陰影部分的概率為：\(P=\frac{A_2}{A_1}=\frac{A_2}{4}\)
  • 從正方形區域抽樣 n 個點，n儘可能大，則來自陰影部分點的期望為：\(nP=\frac{nA_2}{4}\)；
  • 如果實際上滿足上述條件的點 有 m 個，則令 \(m\approx nP\)
  • 得到：\(A_2\approx \frac{4m}{n}\)

程式碼與 6.1 相近。

6.4 求不規則積分

近似求積分是蒙特卡洛在工程和科學問題中最重要的應用。很多積分是沒有解析的積分（即可以計算出來的積分），特別是多元積分，而只能用數值方法求一個近似值，蒙特卡洛就是最常用的數值方法。

一元函數步驟如下：

我們要計算一個一元函數的定積分 \(I = \int_a^bf(x)dx\);

  • 從區間 \([a,b]\) 上隨機均勻抽樣 \(x_1,x_2,...,x_n\);

  • 計算 \(Q_n = (b-a)\frac{1}{n}\sum_{i=1}^nf(x_i)\)，即均值乘以區間長度；

    這裡均值乘以區間長度是 實際值，而 I 是期望值

  • 用 \(Q_n\) 近似 \(I\)

大數定律保證了 當\(n\rightarrow\infty,Q_n\rightarrow I\)

多元函數步驟如下：

我們要計算一個多元函數的定積分 \(I = \int_a^bf(\vec{x})d\vec{x}\)，積分割區域為 \(\Omega\);

  • 從區間 \(\Omega\) 上隨機均勻抽樣 \(\vec{x_1},\vec{x_2},...,\vec{x_n}\);

  • 計算 \(\Omega\) 的體積V（高於三維同樣）：\(V=\int_\Omega{d\vec{x}}\)；

    hh值得注意的是，這一步仍要計算定積分，如果形狀過於複雜，無法求得 V，那麼無法繼續進行，則無法使用蒙特卡洛演演算法。所以只能適用於比較規則的區域，比如圓形，長方體等。

  • 計算 \(Q_n =V \frac{1}{n}\sum_{i=1}^nf(\vec{x_i})\)，即均值乘以區間長度；

    這裡均值乘以區間長度是 實際值，而 I 是期望值

  • 用 \(Q_n\) 近似 \(I\)

下面我們從積分的角度再來看看 蒙特卡洛近似求 pi

  • 定義一個二元函數 \(f(x,y)=\begin{cases} 1 \ \ if點在圓內\\ 0 \ \ if 點在圓外\end{cases}\);
  • 定義一個區間 \(\Omega=[-1,1]×[-1,1]\)
  • \(I =\pi {r^2}=\pi\)
  • 接下來用蒙特卡洛近似 I，得到關於 \(\pi\)的算式即可得到近似的\(\pi\);
    • 隨機抽樣 n 個點，記為\((x_1,y_1),...,(x_n,y_n)\)
    • 計算 區域面積 \(V = \int_\Omega{dxdy}=4\)；
    • 計算 \(Q_n =V \frac{1}{n}\sum_{i=1}^nf(x_i,y_i)\)
    • 蒙特卡洛近似 Q 與 I 近似相等：\(\pi=Q_n=\int_\Omega{f(x,y)}{dxdy}\)

這是從蒙特卡洛積分的角度得到的pi，6.1 中則是從蒙特卡洛概率和期望的角度得到的。

6.5 用蒙特卡洛近似期望

這個方法對於統計學和機器學習很有用。

  • 定義 X 是 d 維的隨機變數，函數 p(x) 是一個PDF，概率密度函數；
  • 函數 \(f(x)\) 的期望：\(\mathbb{E}_{x\sim{p}}[f(X)]=\int_{R^d}f(X)\cdotp(x)dx\)
  • 直接以上面的方式求期望可能並不容易，所以通常使用蒙特卡洛近似求期望：
    1. 隨機抽樣：根據概率密度函數 \(p(x)\) 進行隨機抽樣，記為\(X_1,X_2,...,X_n\)；
    2. 計算 \(Q_n =\frac{1}{n}\sum_{i=1}^nf(x_i)\)
    3. 用 Q 近似 期望\(\mathbb{E}_{x\sim{p}}[f(X)]\)

6.6 總結 | 蒙特卡洛演演算法的思想

我的想法是儘量精簡，即：

模擬---抽樣---估值，通過模擬出來的大量樣本集或者隨機過程，以隨機抽樣的方式，去近似我們想要研究的實際問題物件。

補充蒙特卡洛相關：

  • 蒙特卡洛是摩洛哥的賭場；

  • 蒙特卡洛演演算法得到的結果通常是錯誤的，但很接近真實值，對於對精度要求不高的機器學習已經足夠。

    隨機梯度下降就是一種蒙特卡洛演演算法，用隨機的梯度近似真實的梯度，不準確但是降低了計算量。

  • 蒙特卡洛是一類隨機演演算法，除此以外還有很多隨機演演算法，比如拉斯維加斯演演算法（結果總是正確的演演算法）

x. 參考教學