使用PHP求最大奇約數的和

本篇文章介紹一下使用PHP如何求最大奇約數的和。有一定的參考價值，有需要的朋友可以參考一下，希望對大家有所幫助。

小易是一個數論愛好者，並且對於一個數的奇數約數十分感興趣。一天小易遇到這樣一個問題： 定義函數f(x)為x最大的奇數約數，x為正整數。 例如:f(44) = 11.

現在給出一個N，需要求出 f(1) + f(2) + f(3)…….f(N)

例如： N = 7

f(1) + f(2) + f(3) + f(4) + f(5) + f(6) + f(7) = 1 + 1 + 3 + 1 + 5 + 3 + 7 = 21

小易計算這個問題遇到了困難，需要你來設計一個演算法幫助他。

<?php
$num = trim(fgets(STDIN));

function jNum($num){
        $m = $num/2;
        $res = 1;
        if($num&0x1 == 1){//如果他本身就是個奇數，那麼他的最大奇約數就是他本身
                $res = $num;
                goto HELL;
        }
        for($i = 1; $i<=$m; $i=$i+2){//如果不是，那麼就從1開始一直往上除，每次+2（奇數）
                if($num%$i==0){
                        $res = $i;
                }
        }
        HELL:
        return $res;
}

function jNum2($num)
{
        $res = 0;

        for($i=1;$i<=$num;$i++){
                if(($i&0x1) == 1){//如果他本身就是個奇數，那麼他的最大奇約數就是他本身
                        $res+=$i;
                }else{
                        $n = $i;
                        while(true){//優化，從最大的數開始往下除
                                $n = $n>>1;
                                if(($n&0x1) == 1){
                                        $res+=$n;
                                        break;
                                }
                        }
                }
        }

        HELL:
        return $res;
}

function jNum3($num){//公式法
        if($num == 1){
                return 1;
        }
        if(($num&0x1) == 0){
                return jNum3($num>>1)+$num*$num/4;
        }else{
                return jNum3($num-1)+$num;
        }

}
//$sum = 0;
//for($i = 1; $i<=$num; $i++){
//      $sum+=jNum($i);
//}
//echo $sum;

//echo jNum2($num);

echo jNum3($num);

開始常規思路，一直偵錯的方法1，一直超時，改為方法2，還是超時，沒有什麼本質區別。

換思路。。

求sum(i)的過程中，如果i 為奇數可以直接求，就是 i 本身，即f(i) = i。

問題就是求所有f(i), i為偶數的和。

因為是最大奇約數，所以f(2k) = f(k)，所以f(2) + f(4) + … + f(2k) = f(1) + f(2) + … + f(k);

所以，數學歸納法，可以求出通用公式

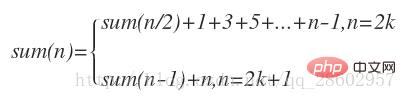
這個做法還是不容易想到的。。。這麼BT的題。。

本文轉載自：https://blog.csdn.net/qq_28602957/article/details/77914402

推薦學習：PHP視訊教學

以上就是使用PHP求最大奇約數的和的詳細內容，更多請關注TW511.COM其它相關文章！