學習總結

文章目錄

學習總結
一、三角分解（LU分解）
二、QR分解
三、SVD分解
四、SVD影象壓縮
五、SVD手寫體識別
Reference

一、三角分解（LU分解）

1.1 高斯消元

1.2 LU分解原理

1.3 LU分解python程式碼

1.4 LU分解演演算法

二、QR分解

2.1 Schmid 正交化

2.2 使用 Schmid 施密特正交化過程求 QR 分解

2.3 QR分解的栗子

三、SVD分解

3.1 SVD定義

Singular Value Decomposition。
SVD是一種基於矩陣分解的，提取資訊的強大工具，能夠發現資料中的潛在模式。應用領域比如：

隱性語意分析 (Latent Semantic Analysis, LSA) 或隱性語意索引 (Latent Semantic Indexing, LSI)；
推薦系統 (Recommender system)，可以說是最有價值的應用點（不過現在推薦系統很多都是基於深度學習模型）；
矩陣形式資料（主要是影象資料）的壓縮。

3.2 SVD基本理論

（1）線性變換

以2×2的線性變換矩陣為例，現在有一個對角矩陣
$M=\left[\begin{array}{ll}3 & 0 \\ 0 & 1\end{array}\right]$

對角矩陣M是將二維平面上的點（x，y）經過線性變換到另一個點的變換矩陣（變換效果：平面沿著x水平方向進行3倍拉伸，垂直方向沒變化）： $\left[\begin{array}{ll} 3 & 0 \\ 0 & 1 \end{array}\right]\left[\begin{array}{l} x \\ y \end{array}\right]=\left[\begin{array}{c} 3 x \\ y \end{array}\right]$

（2）SVD推導（略）

從幾何角度理解二維SVD：藉助SVD可將一個相互垂直的網路（orthogonal grid）變換到另一個互相垂直的網路。
在這裡插入圖片描述
實際應用中，我們僅需保留著三個比較小的矩陣，就能表示A，不僅節省儲存量，在計算的時候更是減少了計算量。SVD在資訊檢索（隱性語意索引）、影象壓縮、推薦系統、金融等領域都有應用。

（3）SVD栗子

其中正交矩陣的特徵值和特徵向量的求解可以複習線性代數。
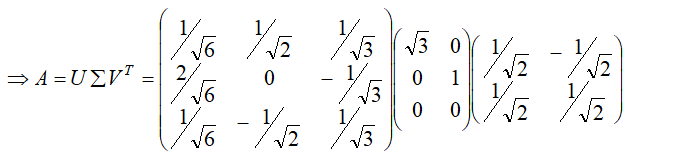
在這裡插入圖片描述

四、SVD影象壓縮

（1）下載cv2：pip install opencv-python。

（2）其中np.linalg.svd(a, full_matrices=1, compute_uv=1)函數：

input引數：
- a是一個形如(M,N)矩陣
- full_matrices的取值是為0或者1，預設值為1，這時u的大小為(M,M)，v的大小為(N,N) 。否則u的大小為(M,K)，v的大小為(K,N) ，K=min(M,N)。
- compute_uv的取值是為0或者1，預設值為1，表示計算u,s,v。為0的時候只計算s。
output引數（三個）：
- u大小為(M,M)，s大小為(M,N)，v大小為(N,N)。
- A = usv
- 其中s是對矩陣a的奇異值分解。s除了對角元素不為0，其他元素都為0，並且對角元素從大到小排列。s中有n個奇異值，一般排在後面的比較接近0，所以僅保留比較大的r個奇異值。

（3）numpy.stack函數：將多個陣列進行堆疊，按照指定的維度，可參考部落格。

# -*- coding: utf-8 -*-
"""
Created on Sat Dec 11 23:14:35 2021

@author: 86493
"""
import cv2
import matplotlib as mpl
import numpy as np
import matplotlib.pyplot as plt

#轉為u8型別
def restore1(u, sigma, v, k):
    
    m = len(u)
    n = len(v)
    a = np.zeros((m, n))
    a = np.dot(u[:, :k], np.diag(sigma[:k])).dot(v[:k, :])
    # s1 =  np.size(u[:, :k])
    # s1+= np.size(np.diag(sigma[:k]))
    # s1+= np.size(np.diag(v[:k, :]))
    # s2 = np.size(a)
    # print("壓縮率：",s1/s2)
    a[a < 0] = 0
    a[a > 255] = 255
    return np.rint(a).astype('uint8')

def SVD(frame,K=10):
    a = np.array(frame)
    #由於是彩色影象，所以3通道。a的最內層陣列為三個數，分別表示RGB，用來表示一個畫素
    u_r, sigma_r, v_r = np.linalg.svd(a[:, :, 0])
    u_g, sigma_g, v_g = np.linalg.svd(a[:, :, 1])
    u_b, sigma_b, v_b = np.linalg.svd(a[:, :, 2])

    
    R = restore1(u_r, sigma_r, v_r, K)
    G = restore1(u_g, sigma_g, v_g, K)
    B = restore1(u_b, sigma_b, v_b, K)
    I = np.stack((R, G, B), axis = 2)
    return I
      

if __name__ == "__main__":
    mpl.rcParams['font.sans-serif'] = [u'simHei']
    mpl.rcParams['axes.unicode_minus'] = False
    # frame = cv2.imread("./liuyifei.bmp",-1)
    frame = cv2.imread("pig.jpg",-1)
    I = SVD(frame,40)
    plt.imshow(I)
    cv2.imwrite("out.bmp",I)

原圖為：
在這裡插入圖片描述
影象壓縮後的圖為：

五、SVD手寫體識別

Reference

（1）SVD-矩陣奇異值分解 —— 原理與幾何意義
（2）SVD應用於影象壓縮 Python程式碼測試
（3）https://www.zhihu.com/question/277311874
（4）矩陣的SVD分解（應用之一：手寫數位識別）
（5）淺談SVD原理以及python實現小demo
（6）SVD（奇異值分解）Python實現（原理清晰）

【機器學習中的矩陣分解】LU分解、QR分解、SVD分解