資料結構和演演算法 (DSA)
通常被認為是一個令人生畏的話題——一種常見的誤解。它們是技術領域最具創新性概念的基礎，對於工作/實習申請者和有經驗的程式設計師的職業發展都至關重要。掌握DSA意味著你能夠使用你的計算和演演算法思維來解決前所未見的問題，併為任何科技公司的價值做出貢獻（包括你自己的！）。通過了解它們，您可以提高程式碼的可維護性、可延伸性和效率。

話雖如此，我決定在CSDN新星計劃挑戰期間將我所瞭解的資料結構和演演算法集中起來。本文旨在使 DSA 看起來不像人們認為的那樣令人生畏。它包括 15 個最有用的資料結構和 15 個最重要的演演算法，可以幫助您在學習中和麵試中取得好成績並提高您的程式設計競爭力。後面等我還會繼續對這些資料結構和演演算法進行進一步詳細地研究講解。

一、資料結構

1. 陣列（Arrays）

陣列是最簡單也是最常見的資料結構。它們的特點是可以通過索引（位置）輕鬆存取元素。

它們是做什麼用的？

想象一下有一排劇院椅。每把椅子都分配了一個位置（從左到右），因此每個觀眾都會從他將要坐的椅子上分配一個號碼。這是一個陣列。將問題擴充套件到整個劇院（椅子的行和列），您將擁有一個二維陣列（矩陣）！

特性

• 元素的值按順序放置，並通過從 0 到陣列長度的索引存取；
• 陣列是連續的記憶體塊；
• 它們通常由相同型別的元素組成（這取決於程式語言）；
• 元素的存取和新增速度很快；搜尋和刪除不是在 O(1) 中完成的。

2. 連結串列（Linked Lists）

連結串列是線性資料結構，就像陣列一樣。連結串列和陣列的主要區別在於連結串列的元素不儲存在連續的記憶體位置。它由節點組成——實體儲存當前元素的值和下一個元素的地址參照。這樣，元素通過指標連結。

它們是做什麼用的？

連結串列的一個相關應用是瀏覽器的上一頁和下一頁的實現。雙連結串列是儲存使用者搜尋顯示的頁面的完美資料結構。

特性

• 它們分為三種型別：單獨的、雙重的和圓形的；
• 元素不儲存在連續的記憶體塊中；
• 完美的優秀記憶體管理（使用指標意味著動態記憶體使用）；
• 插入和刪除都很快；存取和搜尋元素是線上性時間內完成的。

3. 堆疊（Stacks）

堆疊是一種抽象資料型別，它形式化了受限存取集合的概念。該限制遵循 LIFO（後進先出）規則。因此，新增到堆疊中的最後一個元素是您從中刪除的第一個元素。

堆疊可以使用陣列或連結串列來實現。

它們是做什麼用的？

現實生活中最常見的例子是在食堂中將盤子疊放在一起。位於頂部的板首先被移除。放置在最底部的盤子是在堆疊中保留時間最長的盤子。

堆疊最有用的一種情況是您需要獲取給定元素的相反順序。只需將它們全部推入堆疊，然後彈出它們。

另一個有趣的應用是有效括號問題。給定一串括號，您可以使用堆疊檢查它們是否匹配。

特性

• 您一次只能存取最後一個元素（頂部的元素）；
• 一個缺點是，一旦您從頂部彈出元素以存取其他元素，它們的值將從堆疊的記憶體中丟失；
• 其他元素的存取是線上性時間內完成的；任何其他操作都在 O(1) 中。

4. 佇列（Queues）

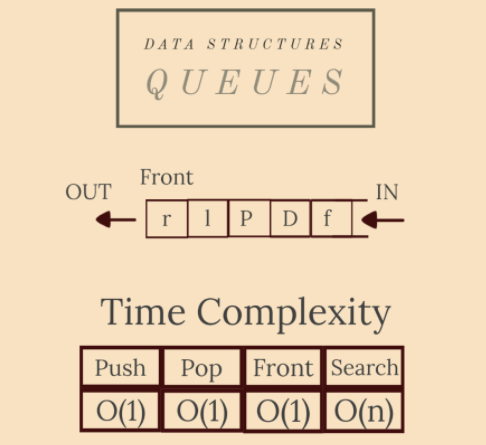
佇列是受限存取集合中的另一種資料型別，就像前面討論的堆疊一樣。主要區別在於佇列是按照FIFO（先進先出）模型組織的：佇列中第一個插入的元素是第一個被移除的元素。佇列可以使用固定長度的陣列、迴圈陣列或連結串列來實現。

它們是做什麼用的？

這種抽象資料型別 (ADT) 的最佳用途當然是模擬現實生活中的佇列。例如，在呼叫中心應用程式中，佇列用於儲存等待從顧問那裡獲得幫助的客戶——這些客戶應該按照他們呼叫的順序獲得幫助。

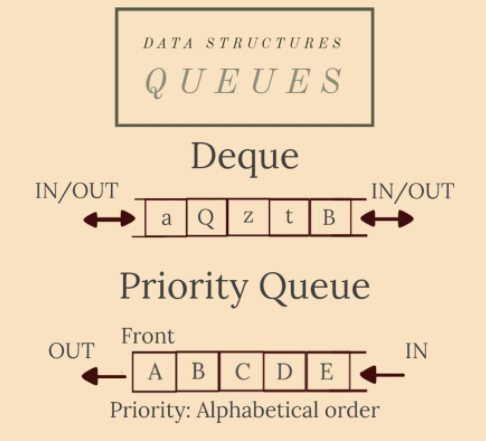
一種特殊且非常重要的佇列型別是優先順序佇列。元素根據與它們關聯的「優先順序」被引入佇列：具有最高優先順序的元素首先被引入佇列。這個 ADT 在許多圖演演算法（Dijkstra 演演算法、BFS、Prim 演演算法、霍夫曼編碼 - 更多關於它們的資訊）中是必不可少的。它是使用堆實現的。

另一種特殊型別的佇列是deque 佇列（雙關語它的發音是「deck」）。可以從佇列的兩端插入/刪除元素。

特性

• 我們只能直接存取引入的「最舊」元素；
• 搜尋元素將從佇列的記憶體中刪除所有存取過的元素；
• 彈出/推播元素或獲取佇列的前端是在恆定時間內完成的。搜尋是線性的。

5. Map 和 雜湊表（Hash Table）

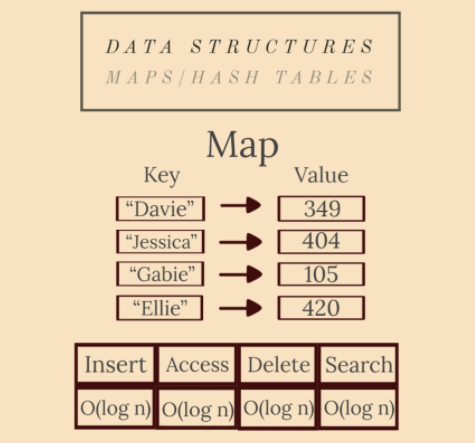
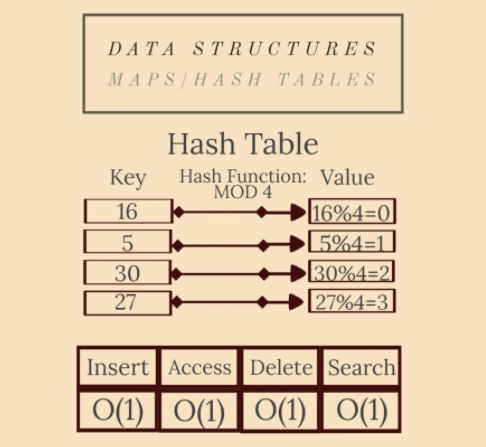
Maps （dictionaries）是包含鍵集合和值集合的抽象資料型別。每個鍵都有一個與之關聯的值。

雜湊表是一種特殊型別的對映。它使用雜湊函數生成一個雜湊碼，放入一個桶或槽陣列：鍵被雜湊，結果雜湊指示值的儲存位置。

最常見的雜湊函數（在眾多雜湊函數中）是模常數函數。例如，如果常數是 6，則鍵 x 的值是x%6。

理想情況下，雜湊函數會將每個鍵分配給一個唯一的桶，但他們的大多數設計都採用了不完善的函數，這可能會導致具有相同生成值的鍵之間發生衝突。這種碰撞總是以某種方式適應的。

它們是做什麼用的？

Maps 最著名的應用是語言詞典。語言中的每個詞都為其指定了定義。它是使用有序對映實現的（其鍵按字母順序排列）。

通訊錄也是一張Map。每個名字都有一個分配給它的電話號碼。

另一個有用的應用是值的標準化。假設我們要為一天中的每一分鐘（24 小時 = 1440 分鐘）分配一個從 0 到 1439 的索引。雜湊函數將為h(x) = x.小時*60+x.分鐘。

特性

• 鍵是唯一的（沒有重複）；
• 抗碰撞性：應該很難找到具有相同鍵的兩個不同輸入；
• 原像阻力：給定值 H，應該很難找到鍵 x，使得h(x)=H；
• 第二個原像阻力：給定一個鍵和它的值，應該很難找到另一個具有相同值的鍵；

術語：

• 「map」：Java、C++；
• 「dictionary」：Python、JavaScript、.NET；
• 「associative array"：PHP。

因為maps 是使用自平衡紅黑樹實現的（文章後面會解釋），所以所有操作都在 O(log n) 內完成；所有雜湊表操作都是常數。

6. 圖表（Graphs）

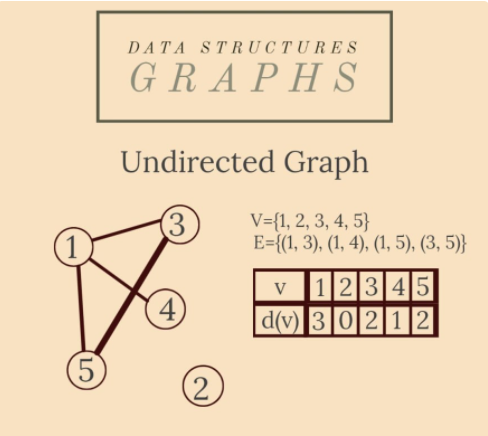
圖是表示一對兩個集合的非線性資料結構：G={V, E}，其中 V 是頂點（節點）的集合，而 E 是邊（箭頭）的集合。節點是由邊互連的值 - 描述兩個節點之間的依賴關係（有時與成本/距離相關聯）的線。

圖有兩種主要型別：有向圖和無向圖。在無向圖中，邊(x, y)在兩個方向上都可用：(x, y)和(y, x)。在有向圖中，邊(x, y)稱為箭頭，方向由其名稱中頂點的順序給出：箭頭(x, y)與箭頭(y, x) 不同。

它們是做什麼用的？

圖是各種型別網路的基礎：社群網路（如 weixin、csdn、weibo），甚至是城市街道網路。社交媒體平臺的每個使用者都是一個包含他/她的所有個人資料的結構——它代表網路的一個節點。weixin 上的好友關係是無向圖中的邊（因為它是互惠的），而在 CSDN 或 weibo上，帳戶與其關注者/關注帳戶之間的關係是有向圖中的箭頭（非互惠）。

特性

圖論是一個廣闊的領域，但我們將重點介紹一些最知名的概念：

• 無向圖中節點的度數是它的關聯邊數；
• 有向圖中節點的內部/外部度數是指向/來自該節點的箭頭的數量；
• 從節點 x 到節點 y 的鏈是相鄰邊的連續，x 是它的左端，y 是它的右邊；
• 一個迴圈是一個鏈，其中 x=y；圖可以是迴圈/非迴圈的；如果 V 的任意兩個節點之間存在鏈，則圖是連通的；
• 可以使用廣度優先搜尋 (BFS) 或深度優先搜尋 (DFS) 遍歷和處理圖，兩者都在 O(|V|+|E|) 中完成，其中 |S| 是集合S 的基數；檢視下面的連結，瞭解圖論中的其他基本資訊。

7. 樹（Trees）

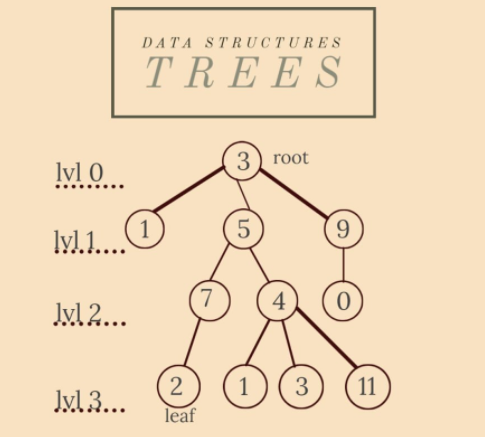
一棵樹是一個無向圖，在連通性方面最小（如果我們消除一條邊，圖將不再連線）和在無環方面最大（如果我們新增一條邊，圖將不再是無環的） . 所以任何無環連通無向圖都是一棵樹，但為了簡單起見，我們將有根樹稱為樹。

根是一個固定節點，它確定樹中邊的方向，所以這就是一切「開始」的地方。葉子是樹的終端節點——這就是一切「結束」的地方。
一個頂點的孩子是它下面的事件頂點。一個頂點可以有多個子節點。一個頂點的父節點是它上面的事件頂點——它是唯一的。

它們是做什麼用的？

我們在任何需要描繪層次結構的時候都使用樹。我們自己的家譜樹就是一個完美的例子。你最古老的祖先是樹的根。最年輕的一代代表葉子的集合。

樹也可以代表你工作的公司中的上下級關係。這樣您就可以找出誰是您的上級以及您應該管理誰。

特性

• 根沒有父級；
• 葉子沒有孩子；
• 根和節點 x 之間的鏈的長度表示 x 所在的級別；
• 一棵樹的高度是它的最高層（在我們的例子中是 3）；
• 最常用的遍歷樹的方法是 O(|V|+|E|) 中的 DFS，但我們也可以使用 BFS；使用 DFS 在任何圖中遍歷的節點的順序形成 DFS 樹，指示我們存取節點的時間。

8. 二元樹（Binary Trees）和二元搜尋樹（Binary Search Trees）

二元樹是一種特殊型別的樹：每個頂點最多可以有兩個子節點。在嚴格二元樹中，除了葉子之外，每個節點都有兩個孩子。具有 n 層的完整二元樹具有所有2ⁿ-1 個可能的節點。

二元搜尋樹是一棵二元樹，其中節點的值屬於一個完全有序的集合——任何任意選擇的節點的值都大於左子樹中的所有值，而小於右子樹中的所有值。

它們是做什麼用的？

BT 的一項重要應用是邏輯表示式的表示和評估。每個表示式都可以分解為變數/常數和運運算元。這種表示式書寫方法稱為逆波蘭表示法 (RPN)。這樣，它們就可以形成一個二元樹，其中內部節點是運運算元，葉子是變數/常數——它被稱為抽象語法樹（AST）。

BST 經常使用，因為它們可以快速搜尋鍵屬性。AVL 樹、紅黑樹、有序集和對映是使用 BST 實現的。

特性

BST 有三種型別的 DFS 遍歷：

• 先序（根、左、右）；
• 中序（左、根、右）；
• 後序（左、右、根）；全部在 O(n) 時間內完成；
• 中序遍歷以升序為我們提供了樹中的所有節點；
• 最左邊的節點是 BST 中的最小值，最右邊的節點是最大值；
• 注意 RPN 是 AST 的中序遍歷；
• BST 具有排序陣列的優點，但有對數插入的缺點——它的所有操作都在 O(log n) 時間內完成。

9. AVL樹（Adelson-Velsky and Landis Trees ）

所有這些型別的樹都是自平衡二元搜尋樹。不同之處在於它們以對數時間平衡高度的方式。

AVL 樹在每次插入/刪除後都是自平衡的，因為節點的左子樹和右子樹的高度之間的模組差異最大為 1。 AVL 以其發明者的名字命名：Adelson-Velsky 和 ​​Landis。

在紅黑樹中，每個節點儲存一個額外的代表顏色的位，用於確保每次插入/刪除操作後的平衡。

在 Splay 樹中，最近存取的節點可以快速再次存取，因此任何操作的攤銷時間複雜度仍然是 O(log n)。

它們是做什麼用的？

AVL 似乎是資料庫理論中最好的資料結構。

RBT（紅黑樹） 用於組織可比較的資料片段，例如文字片段或數位。在 Java 8 版本中，HashMap 是使用 RBT 實現的。計算幾何和函數語言程式設計中的資料結構也是用 RBT 構建的。

在 Windows NT 中（在虛擬記憶體、網路和檔案系統程式碼中），Splay 樹用於快取、記憶體分配器、垃圾收集器、資料壓縮、繩索（替換用於長文字字串的字串）。

特性

• ANY自平衡BST中ANY操作的攤銷時間複雜度為O(log n)；
• 在最壞的情況下，AVL 的最大高度是 1.44 * log2n（為什麼？提示：考慮所有級別都已滿的 AVL 的情況，除了最後一個只有一個元素）；
• AVLs 在實踐中搜尋元素是最快的，但是為了自平衡而旋轉子樹的成本很高；
• 同時，由於沒有旋轉，RBT 提供了更快的插入和刪除；
• 展開樹不需要儲存任何簿記資料。

10.堆（Heaps）

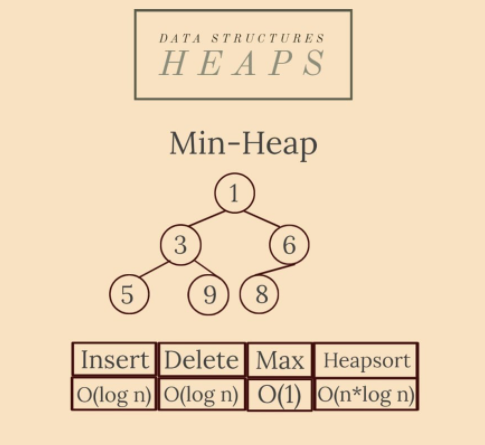
最小堆是一棵二元樹，其中每個節點的值都大於或等於其父節點的值：val[par[x]] <= val[x]，具有堆的 xa 節點，其中val[ x]是它的值，par[x] 是它的父級。

還有一個實現相反關係的最大堆。

二元堆積是一棵完整的二元樹（它的所有層都被填充，除了最後一層）。

它們是做什麼用的？

正如我們幾天前討論過的，優先佇列可以使用二元堆積有效地實現，因為它支援 O(log n) 時間內的 insert()、delete()、extractMax() 和 reduceKey() 操作。這樣，堆在圖演演算法中也是必不可少的（因為優先順序佇列）。

任何時候您需要快速存取最大/最小專案，堆都是最好的選擇。

堆也是堆排序演演算法的基礎。

特性

• 它總是平衡的：無論何時我們在結構中刪除/插入一個元素，我們只需要「篩選」/「滲透」它直到它處於正確的位置；
• 節點k > 1的父節點是[k/2]（其中 [x] 是 x 的整數部分），其子節點是2k和2k+1；
• 設定優先順序佇列的替代方案，ordered_map（在 C++ 中）或任何其他可以輕鬆允許存取最小/最大元素的有序結構；
• 根優先，因此其存取的時間複雜度為O(1)，插入/刪除在O(log n)中完成；建立一個堆是在 O(n) 中完成的；O(n*log n)中的堆排序。

11.字典樹（Tries）

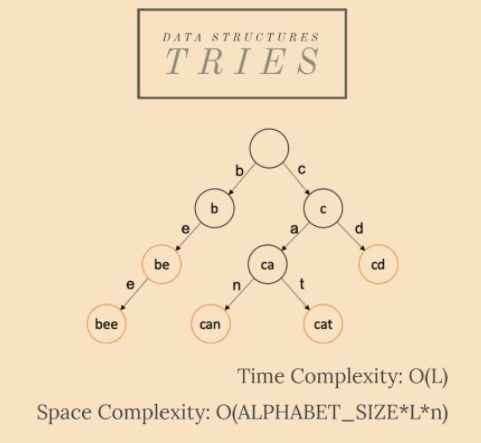
trie 是一種高效的資訊檢索資料結構。也稱為字首樹，它是一種搜尋樹，允許以 O(L) 時間複雜度插入和搜尋，其中 L 是鍵的長度。

如果我們將金鑰儲存在一個平衡良好的 BST 中，它將需要與 L * log n 成正比的時間，其中 n 是樹中的金鑰數量。這樣，與 BST 相比，trie 是一種更快的資料結構（使用 O(L)），但代價是 trie 儲存要求。

它們是做什麼用的？

樹主要用於儲存字串及其值。它最酷的應用程式之一是在 Google 搜尋欄中鍵入自動完成和自動建議。特里是最好的選擇，因為它是最快的選擇：如果我們不使用特里，更快的搜尋比節省的儲存更有價值。

通過在字典中查詢單詞或在同一文字中查詢該單詞的其他範例，也可以使用 trie 來完成鍵入單詞的正字法自動更正。

特性

• 它有一個鍵值關聯；鍵通常是一個單詞或它的字首，但它可以是任何有序列表；
• 根有一個空字串作為鍵；
• 節點值與其子節點值之間的長度差為 1；這樣，根的子節點將儲存長度​​為 1 的值；作為結論，我們可以說來自第 k 層的節點 x 具有長度k 的值；
• 正如我們所說，插入/搜尋操作的時間複雜度是 O(L)，其中 L 是鍵的長度，這比 BST 的 O(log n) 快得多，但與雜湊表相當；

空間複雜度實際上是一個缺點：O(ALPHABET_SIZE*L*n)。

12. 段樹（Segment Trees）

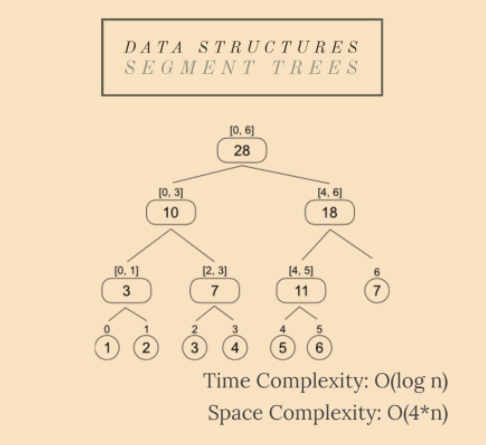
段樹是一個完整的二元樹，可以有效地回答查詢，同時仍然可以輕鬆修改其元素。

給定陣列中索引 i 上的每個元素代表一個用[i, i]間隔標記的葉子。將其子節點分別標記為[x, y]或[y, z]的節點將具有[x, z]區間作為標籤。因此，給定 n 個元素（0-indexed），線段樹的根將被標記為[0, n-1]。

它們是做什麼用的？

它們在可以使用分而治之（我們將要討論的第一個演演算法概念）解決的任務中非常有用，並且還可能需要更新其元素。這樣，在更新元素時​​，包含它的任何區間也會被修改，因此複雜度是對數的。例如，n 個給定元素的總和/最大值/最小值是線段樹最常見的應用。如果元素更新正在發生，二分搜尋也可以使用段樹。

特性

• 作為二元樹，節點 x 將2x和2x+1作為子節點，[x/2]作為父節點，其中[x]是x的整數部分；
• 更新段樹中整個範圍的一種有效方法稱為「延遲傳播」，它也是在 O(log n) 中完成的（有關操作的實現，請參見下面的連結）；
• 它們可以是 k 維的：例如，有 q 個查詢來查詢一個矩陣的給定子矩陣的總和，我們可以使用二維線段樹；
• 更新元素/範圍需要 O(log n) 時間；對查詢的回答是恆定的(O(1))；
• 空間複雜度是線性的，這是一個很大的優勢：O(4*n)。

13. 樹狀陣列（Fenwick Trees）

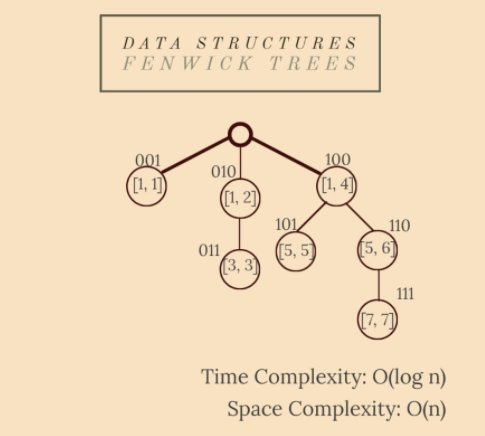
fenwick 樹，也稱為二叉索引樹 (BIT)，是一種也用於高效更新和查詢的資料結構。與 Segment Trees 相比，BITs 需要更少的空間並且更容易實現。

它們是做什麼用的？

BIT 用於計算字首和——第 i 個位置的元素的字首和是從第一個位置到第 i 個元素的總和。它們使用陣列表示，其中每個索引都以二進位制系統表示。例如，索引 10 相當於十進位制系統中的索引 2。

特性

• 樹的構建是最有趣的部分：首先，陣列應該是 1-indexed 要找到節點 x 的父節點，您應該將其索引 x 轉換為二進位制系統並翻轉最右邊的有效位；ex.節點 6 的父節點是 4；

6 = 1*2²+1*2¹+0*2⁰ => 1"1"0 (flip) 
=> 100 = 1*2²+0*2¹+0*2⁰ = 4;

• 最後，ANDing 元素，每個節點都應該包含一個可以新增到字首和的間隔；
• 更新的時間複雜度仍然是 O(log n)，查詢的時間複雜度仍然是 O(1)，但空間複雜度與線段樹的 O(4*n) 相比是一個更大的優勢：O(n)。

14. 並查集（Disjoint Set Union）

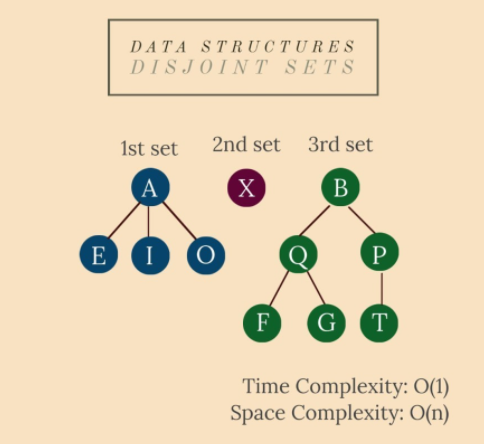
我們有 n 個元素，每個元素代表一個單獨的集合。並查集 (DSU) 允許我們做兩個操作：

1.UNION — 組合任意兩個集合（或者統一兩個不同元素的集合，如果它們不是來自同一個集合）；
2.FIND — 查詢元素來自的集合。

它們是做什麼用的？

並查集（DSU） 在圖論中非常重要。您可以檢查兩個頂點是否來自同一個連線元件，或者甚至可以統一兩個連線元件。

讓我們以城市和城鎮為例。由於人口和經濟增長的鄰近城市正在擴張，它們可以輕鬆建立大都市。因此，兩個城市合併在一起，他們的居民住在同一個大都市。我們還可以通過呼叫 FIND 函數來檢查一個人居住在哪個城市。

特性

• 它們用樹表示；一旦兩組組合在一起，兩個根中的一個成為主根，另一個根的父代是另一棵樹的葉子之一；
• 一種實用的優化是通過高度壓縮樹木；這樣，聯合由最大的樹組成，以輕鬆更新它們的兩個資料（參見下面的實現）；
• 所有操作都在 O(1) 時間內完成。

15. 最小生成樹（Minimum Spanning Trees）

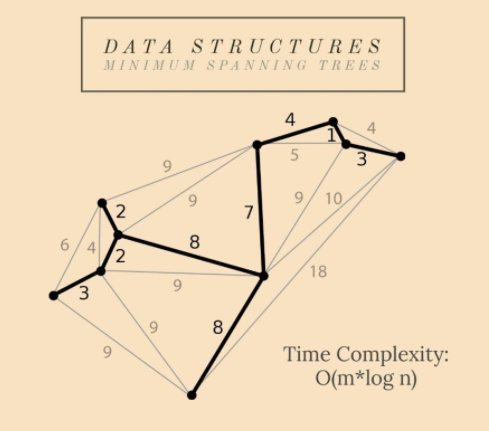
給定一個連通圖和無向圖，該圖的生成樹是一個子圖，它是一棵樹並將所有節點連線在一起。單個圖可以有許多不同的生成樹。加權、連通和無向圖的最小生成樹 (MST) 是權重（成本）小於或等於其他所有生成樹權重的生成樹。生成樹的權重是賦予生成樹每條邊的權重之和。

它們是做什麼用的？

最小生成樹（MST ）問題是一個優化問題，一個最小成本問題。有了路線網，我們可以認為影響n個城市之間建立國道的因素之一是相鄰兩個城市之間的最小距離。

國家路線就是這樣，由道路網路圖的 MST 表示。

特性

作為一棵樹，具有 n 個頂點的圖的 MST 具有 n-1 條邊；可以使用以下方法解決：

• Prim 演演算法 — 密集圖的最佳選擇（具有 n 個節點且邊數接近n(n-1)/2)的圖）；
• Kruskal 演演算法——主要使用；它是一種基於不相交集聯合的貪婪演演算法（我們後面也將討論它）；
• 構建它的時間複雜度對於 Kruskal 來說是 O(n log n) 或 O(n log m)（這取決於圖），對於 Prim 來說是 O(n²)。

二、演演算法

1.分治演演算法（Divide and Conquer）

分而治之（DAC）本身並不是一個特定的演演算法，而是在深入研究其他主題之前需要了解的重要演演算法類別。它用於解決可以劃分為與原始問題相似但規模較小的子問題的問題。然後 DAC 遞迴地求解它們，最後合併結果以找到問題的解決方案。

它分為三個階段：

• 劃分——將問題分解為子問題；
• 用遞迴解決子問題；
• 合併——子問題的結果到最終解決方案中。

它是幹什麼用的？

分治演演算法（DAC） 的一種實際應用是使用多個處理器進行並行程式設計，因此子問題在不同的機器上執行。

DAC 是許多演演算法的基礎，例如快速排序、合併排序、二分搜尋或快速乘法演演算法。

特性

• 每個 DAC 問題都可以寫成一個遞推關係；因此，必須找到停止遞迴的基本情況；
• 它的複雜度是T(n)=D(n)+C(n)+M(n)，這意味著每個階段都有不同的複雜度，具體取決於問題。

2. 排序演演算法（Sorting Algorithms）

排序演演算法用於根據元素上的比較運運算元重新排列給定元素（來自陣列或列表）。當我們提到一個排序陣列時，我們通常會想到升序（比較運運算元是「<」）。排序有多種型別，具有不同的時間和空間複雜度。其中一些是基於比較的，有些則不是。以下是最流行/最有效的排序方法：

氣泡排序（Bubble Sort）

氣泡排序是最簡單的排序演演算法之一。它基於相鄰元素之間的重複交換（如果它們的順序錯誤）。它是穩定的，它的時間複雜度是 O(n²) 並且它需要 O(1) 輔助空間。

計數排序（Counting Sort）

計數排序不是基於比較的排序。它基本上是使用每個元素的頻率（一種雜湊），確定最小值和最大值，然後在它們之間迭代以根據其頻率放置每個元素。它在 O(n) 中完成，空間與資料範圍成正比。如果輸入範圍不明顯大於元素數量，則它是有效的。

快速排序（Quick Sort）

快速排序是分而治之的一個應用。它基於選擇一個元素作為樞軸（第一個、最後一個或中間值），然後交換元素以將樞軸放置在所有小於它的元素和所有大於它的元素之間。它沒有額外的空間和 O(n*log n) 時間複雜度——基於比較的方法的最佳複雜度。

歸併排序（Merge Sort）

歸併排序也是一個分而治之的應用程式。它將陣列分成兩半，對每一半進行排序，然後合併它們。它的時間複雜度也是 O(n*log n)，所以它也像 Quick Sort 一樣超快，但不幸的是它需要 O(n) 額外空間來同時儲存兩個子陣列，最後合併它們。

基數排序（Radix Sort）

基數排序使用計數排序作為子程式，因此它不是基於比較的演演算法。我們怎麼知道CS是不夠的？假設我們必須對[1, n²] 中的元素進行排序。使用 CS，我們需要 O(n²)。我們需要一個線性演演算法——O(n+k)，其中元素在[1, k]範圍內。它從最不重要的一個（單位）開始，到最重要的（十、百等）對元素進行逐位排序。額外空間（來自 CS）：O(n)。

3. 搜尋演演算法（Searching Algorithms）

搜尋演演算法旨在檢查資料結構中元素的存在，甚至返回它。有幾種搜尋方法，但這裡是最受歡迎的兩種：

線性搜尋（Linear Search）

該演演算法的方法非常簡單：您從資料結構的第一個索引開始搜尋您的值。您將它們一一比較，直到您的值和當前元素相等。如果該特定值不在 DS 中，則返回 -1。

時間複雜度：O(n)

二分查詢（Binary Search）

BS 是一種基於分而治之的高效搜尋演演算法。不幸的是，它只適用於排序的資料結構。作為一種 DAC 方法，您連續將 DS 分成兩半，並將搜尋中的值與中間元素的值進行比較。如果它們相等，則搜尋結束。無論哪種方式，如果您的值大於/小於它，搜尋應該繼續在右/左半部分。

時間複雜度：O(log n)

4. 埃氏篩法（Sieve of Eratosthenes）

給定一個整數 n，列印所有小於或等於 n 的素數。
Eratosthenes 篩法是解決這個問題的最有效的演演算法之一，它完美地適用於小於10.000.000 的n 。

該方法使用頻率列表/對映來標記[0, n]範圍內每個數位的素數：如果 x 是素數，則ok[x]=0，否則ok[x]=1。

我們開始從列表中選擇每個素數，並用 1 標記列表中的倍數——這樣，我們選擇未標記的 (0) 數。最後，我們可以在 O(1) 中輕鬆回答任意數量的查詢。

經典演演算法在許多應用中都是必不可少的，但我們可以進行一些優化。首先，我們很容易注意到 2 是唯一的偶素數，因此我們可以單獨檢查它的倍數，然後在範圍內迭代以找到從 2 到 2 的素數。其次，很明顯，對於數位 x，我們之前在迭代 2、3 等時已經檢查了 2x、3x、4x 等。這樣，我們的乘數檢查 for 迴圈每次都可以從 x² 開始。最後，即使這些倍數中有一半是偶數，而且我們也在迭代奇素數，因此我們可以在倍數檢查迴圈中輕鬆地從 2x 迭代到 2x。

空間複雜度：O(n)
時間複雜度：O(n*log(log n)) 用於經典演演算法，O(n) 用於優化演演算法。

5. 字串匹配演演算法（Knuth-Morris-Pratt）

給定長度為 n 的文字和長度為 m 的模式，找出文字中所有出現的模式。

Knuth-Morris-Pratt 演演算法 (KMP) 是解決模式匹配問題的有效方法。
天真的解決方案基於使用「滑動視窗」，每次設定新的起始索引時，我們都會比較字元與字元，從文字的索引 0 開始到索引 nm。這樣，時間複雜度是 O(m*(n-m+1))~O(n*m)。

KMP 是對樸素解決方案的優化：它在 O(n) 中完成，並且當模式具有許多重複的子模式時效果最佳。因此，它也使用滑動視窗，但不是將所有字元與子字串進行比較，而是不斷尋找當前子模式的最長字尾，這也是它的字首。換句話說，每當我們在某些匹配後檢測到不匹配時，我們就已經知道下一個視窗文字中的某些字元。因此，再次匹配它們是沒有用的，因此我們重新開始匹配文字中具有該字首後的字元的相同字元。我們怎麼知道我們應該跳過多少個字元？好吧，我們應該構建一個預處理陣列，告訴我們應該跳過多少個字元。

6.貪婪演演算法（Greedy）

Greedy 方法多用於需要優化且區域性最優解導致全域性最優解的問題。

也就是說，當使用 Greedy 時，每一步的最優解都會導致整體最優解。然而，在大多數情況下，我們在一個步驟中做出的決定會影響下一步的決定列表。在這種情況下，必須用數學方法證明演演算法。Greedy 也會在一些數學問題上產生很好的解決方案，但不是全部（可能無法保證最佳解決方案）！

貪婪演演算法通常有五個組成部分：

• 候選集——從中建立解決方案；
• 選擇函數——選擇最佳候選人；
• 可行性函數——可以確定候選人是否能夠為解決方案做出貢獻；
• 一個目標函數——將候選人分配給（部分）解決方案；
• 一個解決方案函數——從部分解決方案構建解決方案。

分數揹包問題

給定n個物品的重量和價值，我們需要將這些物品放入容量為W的揹包中，以獲得揹包中的最大總價值（允許取件物品：一件物品的價值與其重量成正比）。

貪心方法的基本思想是根據它們的價值/重量比對所有專案進行排序。然後，我們可以新增儘可能多的整個專案。當我們發現一件比揹包中剩餘重量 (w1) 重 (w2) 的物品時，我們將對其進行分割：僅取出w2-w1以最大化我們的利潤。保證這個貪心的解決方案是正確的。

7. 動態規劃（Dynamic Programming）

動態規劃 (DP) 是一種類似於分而治之的方法。它還將問題分解為類似的子問題，但它們實際上是重疊和相互依賴的——它們不是獨立解決的。

每個子問題的結果都可以在以後隨時使用，它是使用記憶（預先計算）構建的。DP 主要用於（時間和空間）優化，它基於尋找回圈。

DP 應用包括斐波那契數列、河內塔、Roy-Floyd-Warshall、Dijkstra 等。 下面我們將討論 0-1 揹包問題的 DP 解決方案。

0–1 揹包問題

給定n個物品的重量和價值，我們需要將這些物品放入容量為W的揹包中，以獲得揹包中的最大總值（不允許像貪婪解決方案中的那樣分割物品）。
0-1 屬性是由我們應該選擇整個專案或根本不選擇它的事實給出的。
我們構建了一個 DP 結構作為矩陣dp[i][cw]儲存我們通過選擇總權重為 cw 的 i 個物件可以獲得的最大利潤。很容易注意到我們應該首先用v[i]初始化dp[1][w[i] ]，其中w[i]是第 i 個物件的權重，v[i] 是它的值。
復現如下：

dp[i][cw] = max(dp[i-1][cw], dp[i-1][cw-w[i]]+v[i])

我們稍微分析一下。

dp[i-1][cw]描述了我們沒有在揹包中新增當前物品的情況。dp[i-1][cw-w[i]]+v[i]就是我們新增item的情況。話雖如此，dp[i-1][cw-w[i]]是採用 i-1 個元素的最大利潤：所以它們的重量是當前重量，沒有我們的物品重量。最後，我們將專案的值新增到它。

答案存入dp[n][W]. 通過一個簡單的觀察進行優化：在迴圈中，當前行僅受前一行的影響。因此，將DP結構儲存到矩陣中是不必要的，因此我們應該選擇一個空間複雜度更好的陣列：O(n)。時間複雜度：O(n*W)。

8. 最長公共子序列（Longest Common Subsequence）

給定兩個序列，找出它們中存在的最長子序列的長度。子序列是以相同的相對順序出現的序列，但不一定是連續的。例如，「bcd」、「abdg」、「c」都是「abcdefg」的子序列。

這是動態規劃的另一個應用。LCS 演演算法使用 DP 來解決上述問題。

實際的子問題是要分別從序列 A 中的索引 i 開始，分別從序列 B 中的索引 j 中找到最長公共子序列。

接下來，我們將構建 DP 結構lcs[ ][ ]（矩陣），其中lcs[i][j]是從 A 中的索引 i 開始，分別是 B 中的索引 j 的公共子序列的最大長度。我們將以自頂向下的方式構建它。顯然，解決方案儲存在lcs[n][m] 中，其中 n 是 A 的長度，m 是 B 的長度。

遞推關係非常簡單直觀。為簡單起見，我們將考慮兩個序列都是 1 索引的。首先，我們將初始化lcs[i][0] , 1<=i<=n和lcs[0][j] , 1<=j<=m , 0, 作為基本情況（沒有從 0 開始的子序列）。然後，我們將考慮兩種主要情況：如果A[i]等於B[j]，則lcs[i][j] = lcs[i-1][j-1]+1（比之前的 LCS 多一個相同的字元）。否則，它將是lcs[i-1][j]（如果不考慮A[i]）和lcs[i][j-1]（如果不考慮B[j]）之間的最大值）。

時間複雜度：O(n*m)
附加空間：O(n*m)

9. 最長遞增子序列（Longest Increasing Subsequence）

給定一個包含 n 個元素的序列 A，找到最長子序列的長度，使其所有元素按遞增順序排序。子序列是以相同的相對順序出現的序列，但不一定是連續的。例如，「bcd」、「abdg」、「c」是「abcdefg」的子序列。

LIS 是另一個可以使用動態規劃解決的經典問題。

使用陣列l[ ]作為 DP 結構來尋找遞增子序列的最大長度，其中l[i]是包含A[i]的遞增子序列的最大長度，其元素來自[A[i] ], ..., A[n]] 子序列。l[i]為 1，如果A[i]之後的所有元素比它小。否則，在 A[i] 之後大於它的所有元素之間的最大值為 1+。顯然，l[n]=1，其中 n 是 A 的長度。 實現是自底向上的（從末尾開始）。

在搜尋當前元素之後的所有元素之間的最大值時出現了一個優化問題。我們能做的最好的事情是二分搜尋最大元素。

為了找到現在已知的最大長度的子序列，我們只需要使用一個額外的陣列ind[]，它儲存每個最大值的索引。

時間複雜度：O(n*log n)
附加空間：O(n)

10.凸包演演算法（Convex Hull）

給定同一平面中的一組 n 個點，找到包含所有給定點（位於多邊形內部或其邊上）的最小面積凸多邊形。這種多邊形稱為凸包。凸包問題是一個經典的幾何，在現實生活中有很多應用。例如，碰撞避免：如果汽車的凸包避免碰撞，那麼汽車也能避免碰撞。路徑的計算是使用汽車的凸表示完成的。形狀分析也是在凸包的幫助下完成的。這樣，影象處理很容易通過匹配模型的凸缺陷樹來完成。

有一些演演算法用於尋找凸包，如 Jarvis 演演算法、Graham 掃描等。今天我們將討論 Graham 掃描和一些有用的優化。

格雷厄姆掃描按極角對點進行排序——由某個點和其他選定點確定的線的斜率。然後用一個棧來儲存當前時刻的凸包。當一個點 x 被壓入堆疊時，其他點會被彈出堆疊，直到 x 與最後兩個點所確定的線形成小於 180° 的角度。最後，引入堆疊的最後一個點關閉多邊形。由於排序，這種方法的時間複雜度為 O(n*log n)。但是，這種方法在計算斜率時會產生精度誤差。

一種改進的解決方案具有相同的時間複雜度，但誤差較小，按座標（x，然後是 y）對點進行排序。然後我們考慮由最左邊和最右邊的點形成的線，並將問題分為兩個子問題。最後，我們在這條線的每一邊找到了凸包。所有給定點的凸包是兩個包的重聚。

11. 圖遍歷（Graph Traversals）

遍歷圖的問題是指以特定順序存取所有節點，通常沿途計算其他有用資訊。

廣度優先搜尋（Breadth-First Search）

廣度優先搜尋 (BFS) 演演算法是確定圖是否連通的最常用方法之一——或者換句話說，查詢 BFS 源節點的連通分量。

BFS 還用於計算源節點和所有其他節點之間的最短距離。BFS 的另一個版本是 Lee 演演算法，用於計算網格中兩個單元格之間的最短路徑。

該演演算法首先存取源節點，然後存取將被推入佇列的鄰居。佇列中的第一個元素被彈出。我們將存取它的所有鄰居，並將之前未存取的鄰居推入佇列。重複該過程直到佇列為空。當佇列為空時，表示所有可達頂點都已存取完畢，演演算法結束。

深度優先搜尋（Depth-First Search）

深度優先搜尋 (DFS) 演演算法是另一種常見的遍歷方法。在檢查圖形的連通性時，它實際上是最好的選擇。

首先，我們存取根節點並將其壓入堆疊。雖然堆疊不為空，但我們檢查頂部的節點。如果該節點有未存取的鄰居，則選擇其中一個並將其壓入堆疊。否則，如果它的所有鄰居都被存取過，我們就會彈出這個節點。當堆疊變空時，演演算法結束。

經過這樣的遍歷，就形成了一個DFS樹。DFS 樹有很多應用；最常見的一種是儲存每個節點的「開始」和「結束」時間——它進入堆疊的時刻，分別是它從堆疊中彈出的時刻。

12. 弗洛依德演演算法（Floyd-Warshall）

Floyd-Warshall / Roy-Floyd 演演算法解決了所有對最短路徑問題：找到給定邊加權有向圖中每對頂點之間的最短距離。

FW 是一個動態規劃應用程式。DP 結構（矩陣）dist[ ][ ]用輸入圖矩陣初始化。然後我們將每個頂點視為其他兩個節點之間的中間體。最短路徑在每兩對節點之間更新，任何節點 k 作為中間頂點。如果 k 是 i 和 j 之間排序路徑中的中間值，則dist[i][j]成為dist[i][k]+dist[k][j]和dist[i][j]之間的最大值。

時間複雜度：O(n³)
空間複雜度：O(n²)

13. Dijkstra 演演算法和 Bellman-Ford 演演算法

迪傑斯特拉（Dijkstra） 演演算法

給定一個圖和圖中的一個源頂點，找出從源到給定圖中所有頂點的最短路徑。

Dijkstra 演演算法用於在加權圖中找到這樣的路徑，其中所有的權重都是正的。

Dijkstra 是一種貪婪演演算法，它使用以源節點為根的最短路徑樹（SPT）。SPT 是一種自平衡二元樹，但該演演算法可以使用堆（或優先順序佇列）來實現。我們將討論堆解決方案，因為它的時間複雜度是 O(|E|*log |V|)。這個想法是使用圖形的鄰接列表表示。這樣，節點將使用 BFS （廣度優先搜尋）在 O(|V|+|E|) 時間內遍歷。

所有頂點都用 BFS 遍歷，那些最短距離尚未最終確定的頂點被儲存到最小堆（優先佇列）中。

建立最小堆並將每個節點連同它們的距離值一起推入其中。然後，源成為距離為 0 的堆的根。其他節點將無限分配為距離。當堆不為空時，我們提取最小距離值節點 x。對於與 x 相鄰的每個頂點 y，我們檢查 y 是否在最小堆中。在這種情況下，如果距離值大於 (x, y) 的權重加上 x 的距離值，那麼我們更新 y 的距離值。

貝爾曼-福特（Bellman-Ford）演演算法

正如我們之前所說，Dijkstra 僅適用於正加權圖。貝爾曼解決了這個問題。給定一個加權圖，我們可以檢查它是否包含負迴圈。如果沒有，那麼我們還可以找到從我們的源到其他源的最小距離（可能為負權重）。

Bellman-Ford 非常適合分散式系統，儘管它的時間複雜度是 O(|V| |E|)。

我們初始化一個 dist[] 就像在 Dijkstra 中一樣。對於 *|V|-1次，對於每個(x, y)邊，如果dist[y] > dist[x] + (x, y) 的權重，那麼我們用它更新dist[y]。

我們重複最後一步以可能找到負迴圈。這個想法是，如果沒有負迴圈，最後一步保證最小距離。如果有任何節點在當前步驟中的距離比上一步中的距離短，則檢測到負迴圈。

14.克魯斯卡爾演演算法（Kruskal’s Algorithm）

我們之前已經討論過什麼是最小生成樹。

有兩種演演算法可以找到圖的 MST：Prim（適用於密集圖）和 Kruskal（適用於大多數圖）。現在我們將討論 Kruskal 演演算法。

Kruskal 開發了一種貪婪演演算法來尋找 MST。它在稀有圖上很有效，因為它的時間複雜度是 O(|E|*log |V|)。

該演演算法的方法如下：我們按權重的遞增順序對所有邊進行排序。然後，選取最小的邊。如果它不與當前 MST 形成迴圈，我們將其包括在內。否則，丟棄它。重複最後一步，直到 MST 中有 |V|-1 條邊。

將邊包含到 MST 中是使用 Disjoint-Set-Union 完成的，這也在前面討論過。

15. 拓撲排序（Topological Sorting）

有向無環圖 (DAG) 只是一個不包含迴圈的有向圖。

DAG 中的拓撲排序是頂點的線性排序，使得對於每個拱形(x, y)，節點 x 出現在節點 y 之前。

顯然，拓撲排序中的第一個頂點是一個入度為 0 的頂點（沒有拱形指向它）。

另一個特殊屬性是 DAG 沒有唯一的拓撲排序。

BFS （廣度優先搜尋）實現遵循此例程：找到一個入度為 0 的節點並將第一個推入排序。該頂點已從圖中刪除。由於新圖也是一個 DAG，我們可以重複這個過程。

在 DFS 期間的任何時候，節點都可以屬於以下三個類別之一：

• 我們完成存取的節點（從堆疊中彈出）；
• 當前在堆疊上的節點；
• 尚未發現的節點。

如果在 DAG 中的 DFS 期間，節點 x 具有到節點 y 的輸出邊，則 y 屬於第一類或第三類。如果 y 在堆疊上，則(x, y)將結束一個迴圈，這與 DAG 定義相矛盾。

這個屬性實際上告訴我們一個頂點在它的所有傳出鄰居都被彈出後從堆疊中彈出。因此，要對圖進行拓撲排序，我們需要跟蹤彈出頂點的逆序列表。

更多相關文章及我的聯絡方式我放在這裡：

https://gitee.com/haiyongcsdn/haiyong

哇，你已經到讀了文章的結尾。感謝您的閱覽！文章篇幅較長，如果有些出錯的地方還請大家批評指正，可在評論區留言或者私信我。

整理不易，最後，不要忘了❤或📑支援一下哦