Go語言封裝qsort快速排序函數
2020-07-16 10:05:17
Ο(n log n) 次比較,在最壞狀況下則需要Ο(n2) 次比較,但這種狀況並不常見。事實上,快速排序通常明顯比其他
Ο(n log n) 演算法更快,因為它的內部迴圈(inner loop)可以在大部分的架構上很有效率地被實現出來,且在大部分真實世界的資料,可以決定設計的選擇,減少所需時間的二次方項之可能性。qsort 快速排序函數是C語言中的一個高階函數,支援用於自定義排序比較函數,可以對任意型別的陣列進行排序。
本節我們為大家簡單的介紹一下C語言中的 qsort 函數,並使用Go語言實現類似功能的 qsort 函數。
認識 qsort 函數
qsort 快速排序函數有<stdlib.h> 標準庫提供,函數的宣告如下:
void qsort(
void* base, size_t num, size_t size,
int (*cmp)(const void*, const void*)
);
- base:引數是要排序陣列的首個元素的地址;
- num:是陣列中元素的個數;
- size:是陣列中每個元素的大小;
- cmp:用於對陣列中任意兩個元素進行排序。
cmp 排序函數的兩個指標引數分別是要比較的兩個元素的地址,如果第一個引數對應的元素大於第二個引數對應的元素則返回結果大於 0,如果兩個元素相等則返回 0,如果第一個元素小於第二個元素則返回結果小於 0。
下面的程式碼展示了使用C語言的 qsort 函數對一個 int 型別的陣列進行排序:
#include <stdio.h>
#include <stdlib.h>
#define DIM(x) (sizeof(x)/sizeof((x)[0]))
static int cmp(const void* a, const void* b) {
const int* pa = (int*)a;
const int* pb = (int*)b;
return *pa - *pb;
}
int main() {
int values[] = { 42, 8, 109, 97, 23, 25 };
int i;
qsort(values, DIM(values), sizeof(values[0]), cmp);
for(i = 0; i < DIM(values); i++) {
printf ("%d ",values[i]);
}
return 0;
}
程式碼說明如下:
- DIM(values) 宏用於計算陣列元素的個數;
- sizeof(values[0]) 用於計算陣列元素的大小;
- cmp 是用於排序時比較兩個元素大小的回撥函數。
使用Go語言實現快速排序函數
1) 快速排序穩定性
快速排序是不穩定的演算法,它不滿足穩定演算法的定義。演算法穩定性可以這樣理解,假設在數列中存在
a[i]=a[j],若在排序之前,a[i] 在 a[j] 前面,並且在排序之後,a[i] 仍然在 a[j] 前面,則這個排序演算法才算是穩定的。2) 快速排序時間複雜度
快速排序的時間複雜度在最壞情況下是O(N²),平均的時間複雜度是O(N*lgN)。這句話很好理解:假設被排序的數列中有 N 個數,遍歷一次的時間複雜度是
O(N),需要遍歷多少次呢?至少lg(N+1) 次,最多 N 次。為什麼最少是 lg(N+1) 次?
快速排序是採用的分治法進行遍歷的,我們將它看作一棵二元樹,它需要遍歷的次數就是二元樹的深度,而根據完全二元樹的定義,它的深度至少是lg(N+1)。因此,快速排序的遍歷次數最少是lg(N+1) 次。為什麼最多是 N 次?
將快速排序看作一棵二元樹,它的深度最大是 N,因此,快讀排序的遍歷次數最多是 N 次。範例程式碼如下:
package main
import (
"fmt"
)
func main() {
Arr := []int{23, 65, 13, 27, 42, 15, 38, 21, 4, 10}
qsort(Arr, 0, len(Arr)-1)
fmt.Println(Arr)
}
/**
快速排序:分治法+遞迴實現
隨意取一個值A,將比A大的放在A的右邊,比A小的放在A的左邊;然後在左邊的值AA中再取一個值B,將AA中比B小的值放在B的左邊,將比B大的值放在B的右邊。以此類推
*/
func qsort(arr []int, first, last int) {
flag := first
left := first
right := last
if first >= last {
return
}
// 將大於arr[flag]的都放在右邊,小於的,都放在左邊
for first < last {
// 如果flag從左邊開始,那麼是必須先從有右邊開始比較,也就是先在右邊找比flag小的
for first < last {
if arr[last] >= arr[flag] {
last--
continue
}
// 交換資料
arr[last], arr[flag] = arr[flag], arr[last]
flag = last
break
}
for first < last {
if arr[first] <= arr[flag] {
first++
continue
}
arr[first], arr[flag] = arr[flag], arr[first]
flag = first
break
}
}
qsort(arr, left, flag-1)
qsort(arr, flag+1, right)
}
執行結果如下:
[4 10 13 15 21 23 27 38 42 65]
分治法策略
快速排序使用分治法策略,分治法就是把一個複雜的問題分解成兩個或更多的相同或相似的子問題,再把子問題分成更小的子問題,直到最後子問題可以簡單的直接求解 (各個擊破),原問題的解即子問題的解的合併。因此分治法的執行步驟為:
- 第一步(分):將原來複雜的問題分解為若干個規模較小、相互獨立、與原問題形式相同的子問題,分解到可以直接求解為止;
- 第二步(治):此時可以直接求解;
- 第三步(合):將小規模的問題的解合併為一個更大規模的問題的解,自底向上逐步求出原來問題的解,如下圖所示。
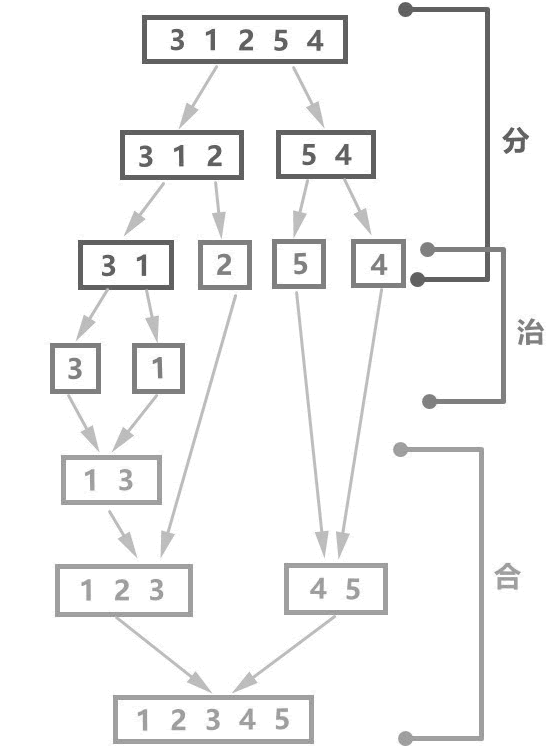
圖:有序子序列兩兩歸並形成新的有序序列