開啟我的收藏夾 -- Python時間序列分析篇

文章目錄
前言
這兩天,又接收到了不少新的訊息。我是越來越佩服「夢想橡皮檫」,檫哥了(開啟周榜/總榜很好找,前排),他居然能用幾年的時間來打磨一個系列。別說收39塊,就是原價99我也買了,不為啥,就憑人家打磨了三年的毅力,我服!!!
想想我自己,曾經也有幾個機會擺在我面前,但是我都放棄了,告訴自己:急流勇退。。。
好吧,我要像檫哥學習,認真的打磨一個系列。
但是我又不知道做什麼系列,深思熟慮之後,那就:「開啟我的收藏夾」系列吧。早晚有一天,我會把這個系列打磨的可以拿來賣。
時間序列分析啊,我這功力不足,就花兩倍的時間來整理吧。
時間序列分析
時間序列預測簡介
時間序列是在定期的時間間隔內記錄度量的序列。
根據頻率,時間序列可以是每年(例如:年度預算),每季度(例如:支出),每週(例如:銷售數量),每天(例如天氣),每小時(例如:股票價格),分鐘(例如:來電提示中的呼入電話),甚至是幾秒鐘(例如:網路流量)。
常用時間序列分析模型
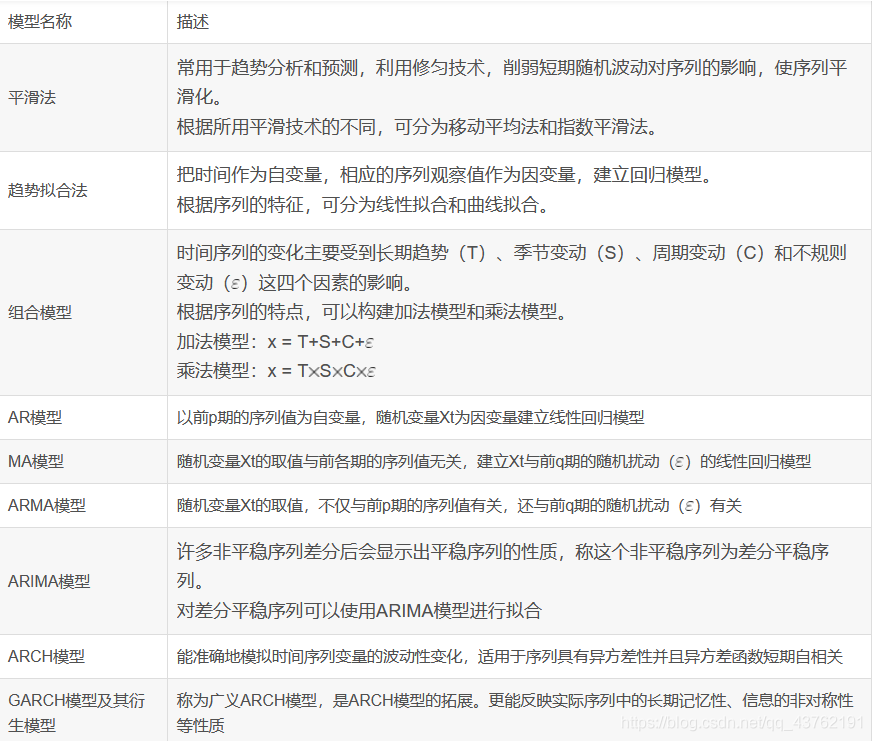
很遺憾,我們今天可能只能講ARIMA模型,或者還能加上一兩個,拭目以待。
ARIMA模型是指將非平穩時間序列轉化為平穩時間序列,然後將結果變數做自迴歸(AR)和自平移(MA)。
資料預處理
時間序列分析之前,需要進行序列的預處理,包括純隨機性和平穩性檢驗。根據檢驗結果可以將序列分為不同的型別,採取不同的分析方法。

這種怎麼弄呢?把我們寫程式碼的思維帶進來,其實沒那麼玄乎,不就是條件判斷嘛:
if 檢驗序列A是白噪聲序列:
return null;
elif 檢驗序列A是平穩非白噪聲序列:
return ARIMA檢驗
else:
轉變為平穩序列
return ARIMA檢驗
至於檢驗方法:
序列檢驗方法
(1)白噪聲檢驗方法
實際上純隨機性序列的樣本自相關係數不會絕對為零,但是很接近零,並在零附近隨機波動。
常用的檢驗統計量有Q統計量、LB統計量,由樣本各延遲期數的自相關係數,可以計算出檢驗統計量,然後計算對應的p值,如果p值大於顯著性水平α(0.05),則表示接受原假設,是純隨機序列,停止分析。
(2)平穩性檢驗方法
如果時間序列在某一常數附近波動且波動範圍有限,即有常數均值和常數方差,並且延遲k期的序列變數的自協方差和自相關係數是相等的,或者說延遲k期的序列變數之間的影響程度是一樣的,則稱該時間序列為平穩序列。
判斷方法一:根據自相關圖、偏自相關圖自己看。這樣難免有失偏頗,何況我們還沒到那一步。
判斷方法二:ARIMA定階。
(1)計算自相關係數(ACF)和偏自相關係數(PACF)
(2)ARMA模型識別,也叫模型定階,由AR(p)模型、MA(q)模型和ARMA(p,q)的自相關係數和偏自相關係數的性質,選擇合適的模型。

(3)估計模型中未知引數的值,並進行引數檢驗
(4)模型檢驗
(5)模型優化
(6)模型應用:進行短期預測。
我們當時也就學了這些(可能是我當時就學了這些)。
(3)非平穩時間序列分析
把所有序列的變化都歸結為四個因素,長期趨勢、 季節變動、 迴圈變動和隨機變動的綜合影響。
隨機時序分析可以建立的模型有 ARIMA模型、殘差自迴歸模型、季節模型、異方差模型等。
通常情況下,我們考慮進行季節因素的分解,也就是將季節變動因素從原時間序列中去除,並生成由剩餘三種因素構成的序列來滿足後續分析需求。
為什麼只進行季節因素的分解?
時間序列中的長期趨勢反映了事物發展規律,是重點研究的物件;
迴圈變動由於週期長,可以看做是長期趨勢的反映;
不規則變動由於不容易測量,通常也不單獨分析。
季節變動有時會讓預測模型誤判其為不規則變動,從而降低模型的預測精度
綜上所述:當一個時間序列具有季節變動特徵時,在預測之前會先將季節因素進行分解。
定義日期標示變數:即先將序列的時間定義好,才能分析其時間特徵。
瞭解序列發展趨勢:即序列圖,確定乘性還是加性
進行季節因素分解
建模
分析結果解讀
預測
如何根據序列圖來判斷模型的乘性或加性?
如果隨著時間的推移,序列的季節波動變得越來越大,則建議使用乘法模型。
如果序列的季節波動能夠基本維持恆定,則建議使用加法模型。
(關於這些,後面用SPSS來講)
(這裡先不講其他的模型,為什麼呢?可以翻到前面去看一下,ARIMA模型的第一步就是使得模型平穩,如果在兩次差分之後還是無法平穩,那我們再議。)
如何使得序列平穩呢?最常見的方式就是差分了。
ARIMA模型
這一塊兒講一些概念,實操的話下面再開一塊兒。其實上面也涉及到不少了了,這裡就補全一下上面遺漏的點吧。
「ARIMA」實際上並不是一整個單詞,而是一個縮寫。其全稱是:Autoregressive Integrated Moving Average Model,即自迴歸移動平均模型。它屬於統計模型中最常見的一種,用於進行時間序列的預測。其原理在於:在將非平穩時間序列轉化為平穩時間序列的過程中,將因變數僅對它的滯後值以及隨機誤差項的現值和滯後值進行迴歸所建立的模型。
ARIMA模型與ARMA模型的區別:ARMA模型是針對平穩時間序列建立的模型。ARIMA模型是針對非平穩時間序列建模,需要對時間序列先做差分,平穩後再建立ARMA模型。
拖尾:始終有非零取值,不會在k大於某個常數後就恆等於零(或在0附近隨機波動)
截尾:在大於某個常數k後快速趨於0為k階截尾
AR模型:自相關係數拖尾,偏自相關係數截尾;
MA模型:自相關係數截尾,偏自相關函數拖尾;
ARMA模型:自相關函數和偏自相關函數均拖尾。
其實截尾拖尾我們這水平也不那麼容易看出來,上面不是說了嘛,還會帶有主觀性。
所以我們還是交給計算機幫我們判斷參考吧。
AR模型對應p,根據偏自相關圖的截尾位置確定p,ACF與PACF圖的橫軸均從0開始,如果PACF在2時還在置信區間以外,從3開始之後均在置信區間以內,則定p為2。MA模型對應q,根據自相關圖的截尾位置確定q,確定方法同p。
範例一:
資料來源準備
無資料或資料品質低,會影響模型預測效果。在建立的一個合理的模型之前,對資料要進行收集,再在蒐集的資料基礎上進行預處理。
有了資料,但是有一部分特徵是演演算法不能直接處理的,還有一部分資料是演演算法不能直接利用的。
讀取出資料集:
import pandas as pd
df = pd.read_csv('jetrail.csv')
df.head()
print(df.shape)
依照上面的程式碼,我們獲得了 2012-2014 年兩年每個小時的乘客數量。為了解釋每種方法的不同之處,以每天為單位構造和聚合了一個資料集。
從 2012 年 8 月- 2013 年 12 月的資料中構造一個資料集。
前 14 個月( 2012 年 8 月- 2013 年 10 月)用作訓練資料,後兩個月(2013 年 11 月 – 2013 年 12 月)用作測試資料。
以每天為單位聚合資料集。
做出時序圖
import pandas as pd
import matplotlib.pyplot as plt
df = pd.read_csv('jetrail.csv', nrows=11856)
# Creating train and test set
# Index 10392 marks the end of October 2013
train = df[0:10392] #訓練資料
test = df[10392:] #測試資料
# Aggregating the dataset at daily level
df['Timestamp'] = pd.to_datetime(df['Datetime'], format='%d-%m-%Y %H:%M') # 4位元年用Y,2位年用y
df.index = df['Timestamp']
df = df.resample('D').mean() # 按天取樣,計算均值
train['Timestamp'] = pd.to_datetime(train['Datetime'], format='%d-%m-%Y %H:%M')
train.index = train['Timestamp']
train = train.resample('D').mean()
test['Timestamp'] = pd.to_datetime(test['Datetime'], format='%d-%m-%Y %H:%M')
test.index = test['Timestamp']
test = test.resample('D').mean()
# Plotting data
train.Count.plot(figsize=(15, 8), title='Daily Ridership', fontsize=14)
test.Count.plot(figsize=(15, 8), title='Daily Ridership', fontsize=14)
plt.show()
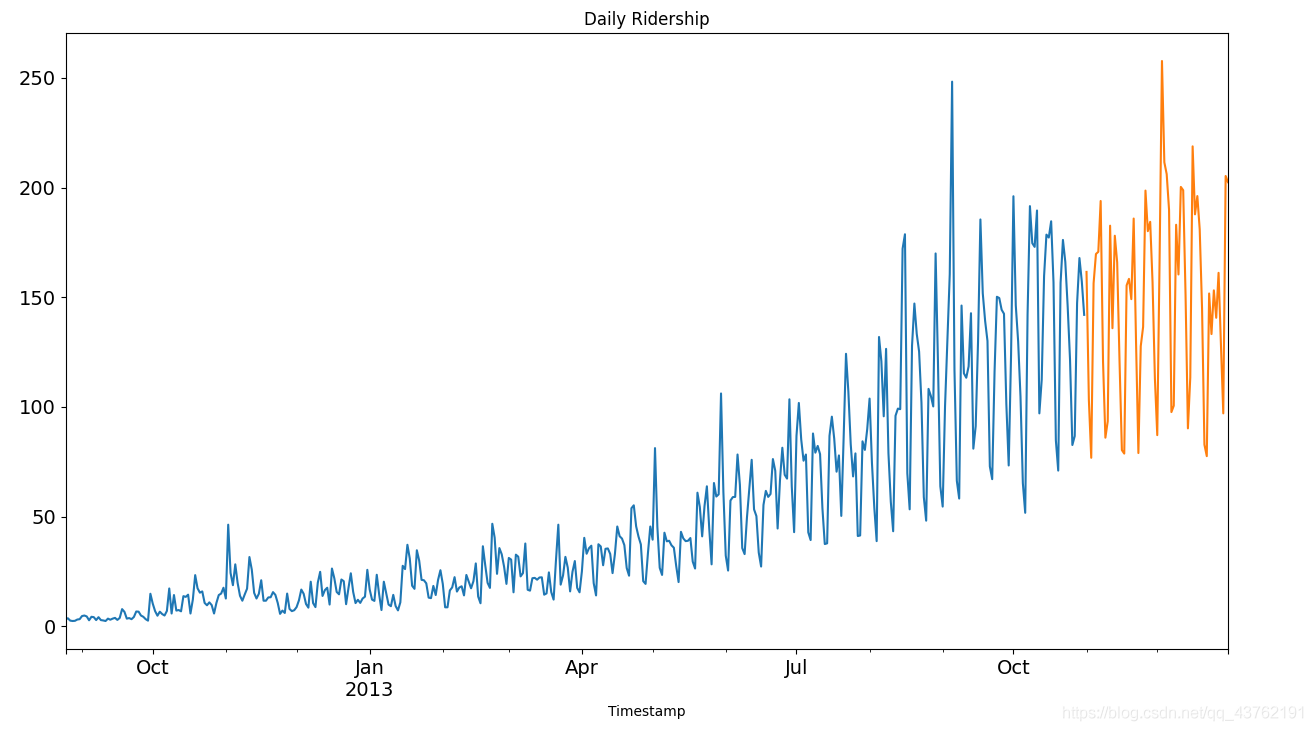
幾種資料分析方法
詳見:點此進入案例來源
我相信,大部分人點過去也會回來的。
其中程式碼做了些許微調,處理了一些警告。
(1)樸素法
如果資料集在一段時間內都很穩定,我們想預測第二天的價格,可以取前面一天的價格,預測第二天的值。這種假設第一個預測點和上一個觀察點相等的預測方法就叫樸素法。
樸素法並不適合變化很大的資料集,最適合穩定性很高的資料集。
(2)簡單平均法
我們經常會遇到一些資料集,雖然在一定時期內出現小幅變動,但每個時間段的平均值確實保持不變。這種情況下,我們可以預測出第二天的價格大致和過去天數的價格平均值一致。這種將預期值等同於之前所有觀測點的平均值的預測方法就叫簡單平均法。
將過去觀察值賦予不同權重的方法就叫做加權移動平均法。加權移動平均法其實還是一種移動平均法,只是「滑動視窗期」內的值被賦予不同的權重,通常來講,最近時間點的值發揮的作用更大了。即
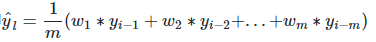
(3)霍爾特(Holt)線性趨勢法
每個時序資料集可以分解為相應的幾個部分:趨勢(Trend),季節性(Seasonal)和殘差(Residual)。任何呈現某種趨勢的資料集都可以用霍爾特線性趨勢法用於預測。
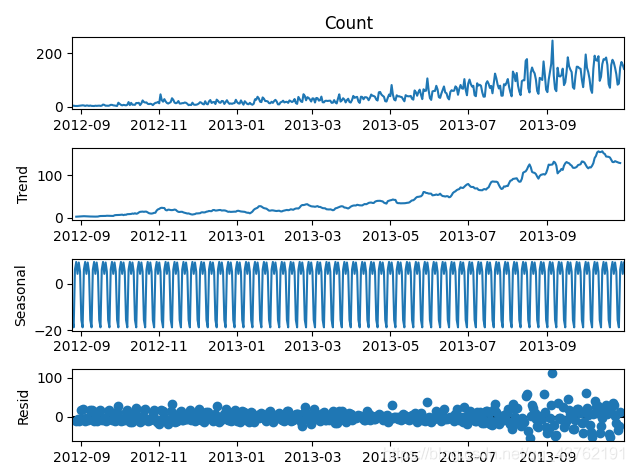
import statsmodels.api as sm
sm.tsa.seasonal_decompose(train['Count']).plot()
result = sm.tsa.stattools.adfuller(train['Count'])
plt.show()
霍爾德線性探測演演算法:
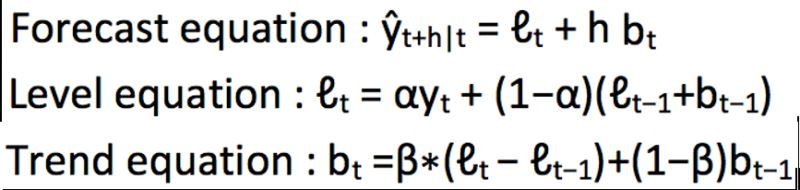
我們將這兩個方程相加,得出一個預測函數。我們也可以將兩者相乘而不是相加得到一個乘法預測方程。當趨勢呈線性增加和下降時,我們用相加得到的方程;當趨勢呈指數級增加或下降時,我們用相乘得到的方程。
實踐操作顯示,用相乘得到的方程,預測結果會更穩定,但用相加得到的方程,更容易理解。
from statsmodels.tsa.api import Holt
y_hat_avg = test.copy()
fit = Holt(np.asarray(train['Count'])).fit(smoothing_level=0.3, smoothing_trend=0.1)
y_hat_avg['Holt_linear'] = fit.forecast(len(test))
plt.figure(figsize=(16, 8))
plt.plot(train['Count'], label='Train')
plt.plot(test['Count'], label='Test')
plt.plot(y_hat_avg['Holt_linear'], label='Holt_linear')
plt.legend(loc='best')
plt.show()
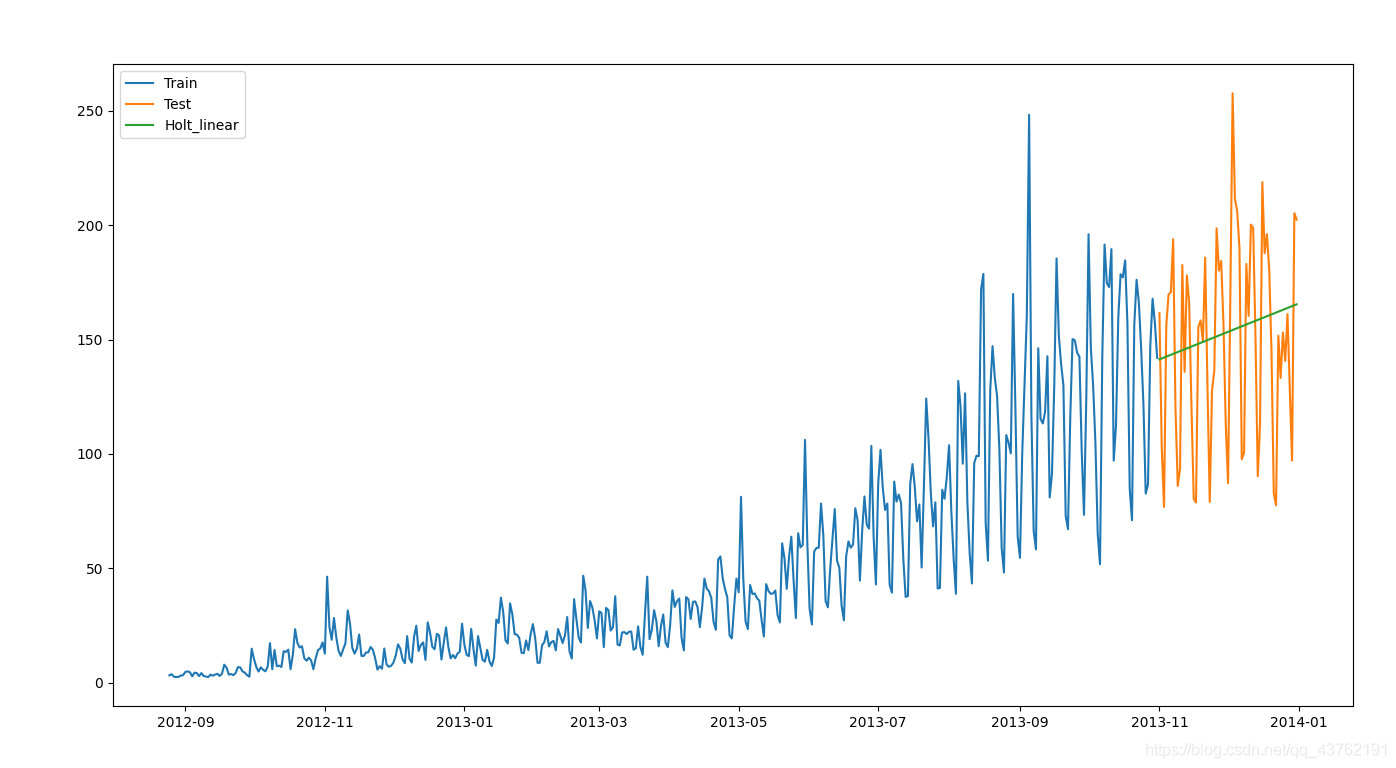
這種方法能夠準確地顯示出趨勢,因此比前面的幾種模型效果更好。如果調整一下引數,結果會更好。
(4)Holt-Winters季節性預測模型
它是一種三次指數平滑預測,其背後的理念就是除了水平和趨勢外,還將指數平滑應用到季節分量上。
Holt-Winters季節性預測模型由預測函數和三次平滑函數——一個是水平函數ℓt,一個是趨勢函數bt,一個是季節分量 st,以及平滑引數α,β和γ。
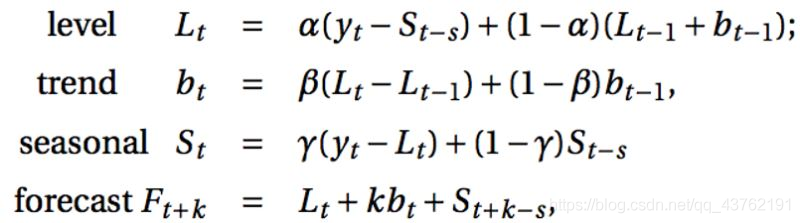
其中 s 為季節迴圈的長度,0≤α≤ 1, 0 ≤β≤ 1 , 0≤γ≤ 1。水平函數為季節性調整的觀測值和時間點t處非季節預測之間的加權平均值。趨勢函數和霍爾特線性方法中的含義相同。季節函數為當前季節指數和去年同一季節的季節性指數之間的加權平均值。
from statsmodels.tsa.api import ExponentialSmoothing
y_hat_avg = test.copy()
fit1 = ExponentialSmoothing(np.asarray(train['Count']), seasonal_periods=7, trend='add', seasonal='add', ).fit()
y_hat_avg['Holt_Winter'] = fit1.forecast(len(test))
plt.figure(figsize=(16, 8))
plt.plot(train['Count'], label='Train')
plt.plot(test['Count'], label='Test')
plt.plot(y_hat_avg['Holt_Winter'], label='Holt_Winter')
plt.legend(loc='best')
plt.show()
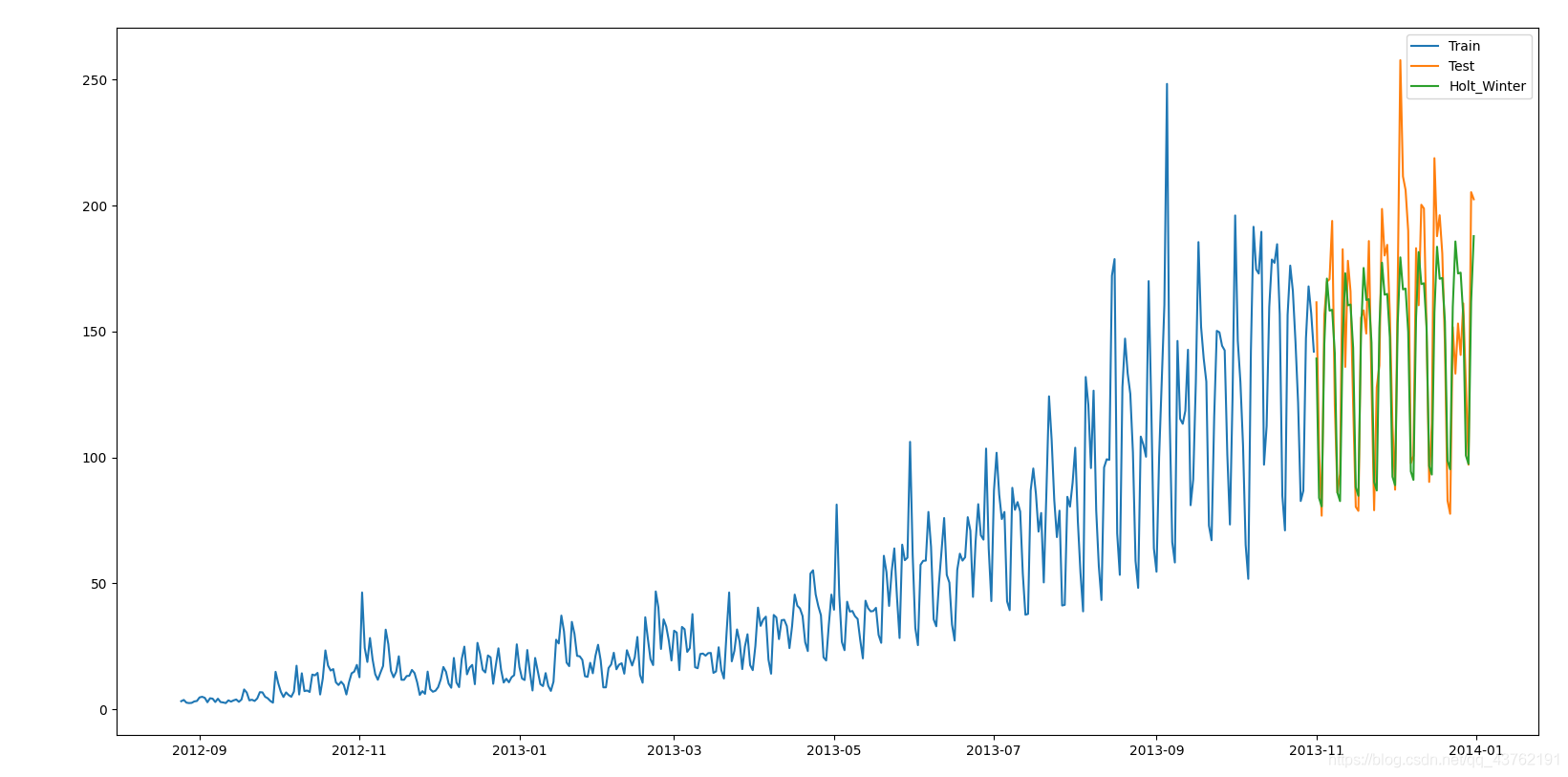
我們可以看到趨勢和季節性的預測準確度都很高。
(5)自迴歸移動平均模型(ARIMA)
指數平滑模型都是基於資料中的趨勢和季節性的描述,而自迴歸移動平均模型的目標是描述資料中彼此之間的關係。ARIMA的一個優化版就是季節性ARIMA。它像Holt-Winters季節性預測模型一樣,也把資料集的季節性考慮在內。
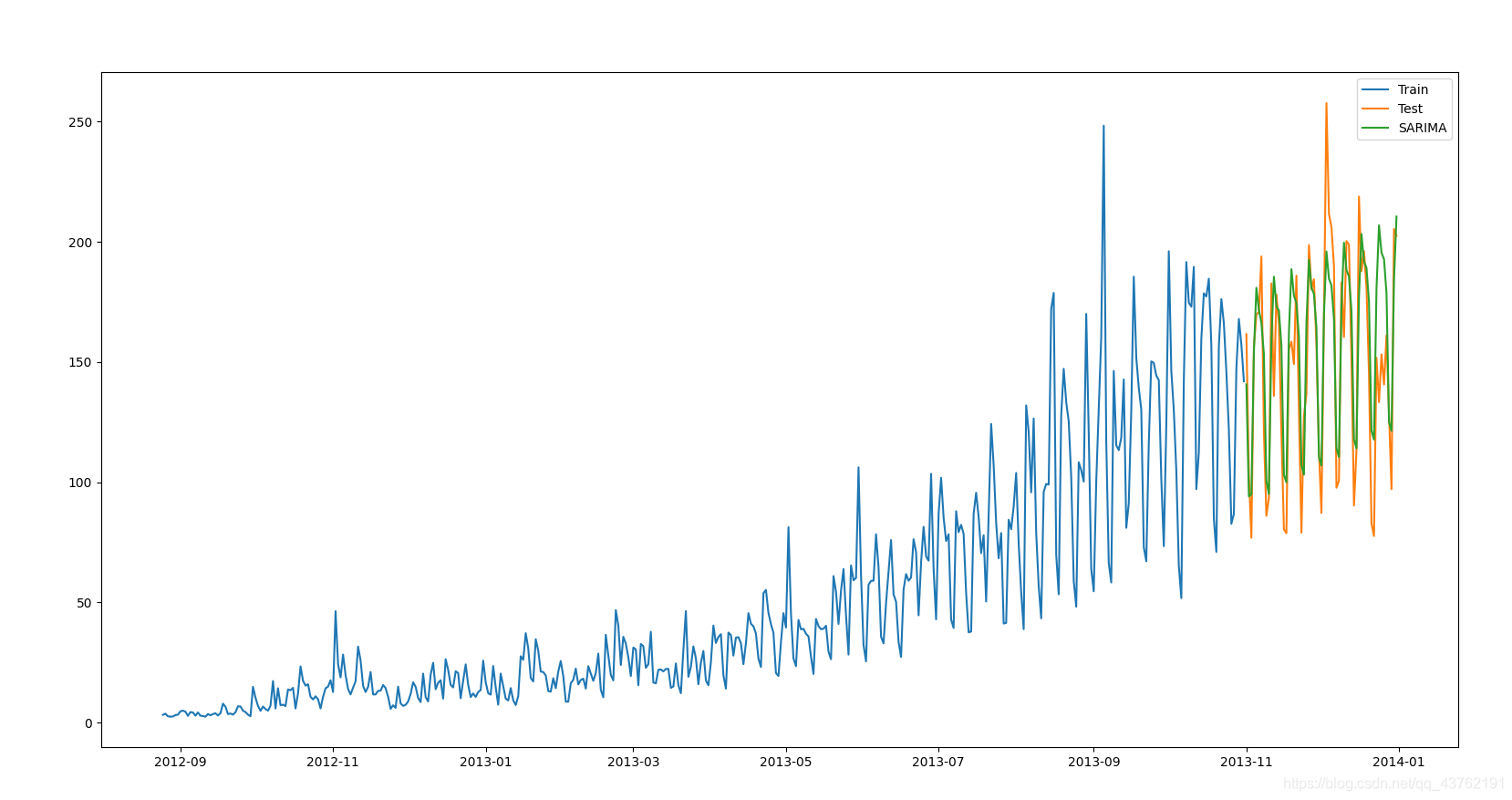
建議你在解決問題時,可以依次試試這幾種模型,看看哪個效果最好。我們從上文也知道,資料集不同,每種模型的效果都有可能優於其它模型。因此,如果一個模型在某個資料集上效果很好,並不代表它在所有資料集上都比其它模型好。
相關概念速查
時間序列分析的性質
頻率、時間跨度、均值、方差、協方差是用來描述時間序列的基本指標。
白噪聲
白噪聲,是不含任何有助於估計資訊(除其方差和高階矩)的時間序列。
平穩性
平穩性是時間序列的一個重要性質。如果一個時間序列是平穩的,那麼發生在時間 t 上的任何衝擊,隨著時間的推移會有一個遞減效應。
最後會消失在時間 t+s,s->∞。
這種特性稱之為均值迴歸。
非平穩的時間序列卻並非如此,衝擊的影響要麼在未來所有的時間持續呈現相同的規模,要麼被看做序列在接下來的時間中「激增」的源頭。
注意白噪聲序列雖然是平穩的,但是平穩序列是不會自動成為白噪聲序列的。要想成為白噪聲,我們需要新增所有的協方差為0的附加條件。
時間序列轉換
差分平穩時間序列差分後平穩化,趨勢平穩序列去趨勢後平穩化,結構突變趨勢的平穩序列通過結構變化去趨勢之後平穩化(更多?往下看就更多)
在差分和去趨勢之前,最常用的轉換方式就是將資料取對數,這樣可以處理一些非線性趨勢序列或將序列的指數趨勢降低到線性趨勢。
當資料呈指數增長時要對資料取自然對數;
差分是將非平穩序列轉換為平穩序列的最常用的方法:
一階差分 ∆y₂ = y₂ - y₁ (意會一下,這裡下標及就找到這倆符號了)
二階差分 ∆²y₂ = ∆y₂ - ∆y₁
再高階差分也沒有什麼意義了,一階差分我們得到的是速度,二階差分我們得到的是加速度,三階?三階差分圖個什麼?
去趨勢是為了消除資料中的線性趨勢或高階趨勢的過程。為了消除時間序列的趨勢,我們進行一個關於常數、時間t、t的高階冪的迴歸。
時間序列的ARMA模型
ARMA模型是用來估計平穩的不規則波動或時間序列季節性變動的最常見的模型。ARMA是移動平均自迴歸模型的簡稱,它是自迴歸模型和移動平均模型的組合。
典型的時間序列的性質
(1)趨勢
經濟時間序列通常包含一個趨勢。
(2)趨勢突變和結構變化
(3)均值上下浮動
(4)衝擊的高永續性
(5)波動不是常數
(6)非平穩
(7)多元時間序列的聯動性
單變數時間序列
估計ARMA模型
自相關函數(ACF)與偏自相關函數(PACF)
自相關函數和偏自相關函數,有助於確定ARMA(p,q)資料生成過程的引數p和q。
Q檢驗
在實踐中,樣本ACF和PACF往往是不確定的,因此發現一個明確的模式是很難的。
為了增加正確選擇滯後期數的機會,我們可以使用另一個工具:基於Q統計量的Q檢驗提供一個更正確的方式來評估正確的滯後期數。
殘差診斷
正確模擬資料生成過程的模型的殘差應該是白噪聲。這意味著它們不應該包含任何有效的資訊。白噪聲所有的自相關函數都等於0,因此使用Q檢驗來檢驗一個時間序列是否是白噪聲只是一個合適但是有限的工具(不看螢幕不看鍵盤盲打一段)。
資訊準則
有時候,會出現好幾種可以選的模型。
這時候,我們選擇最簡約的,往往能夠較好的擬合資料的動態。
時間序列的趨勢
確定性趨勢
隨機性趨勢
隨機和確定性趨勢
在實際應用中估計程式:
檢測趨勢
通過合適的轉換消除趨勢
估計轉換的時間序列
季節性時間序列
包含季節性模式的時間序列不一定是非平穩的,但是,當估計資料生成過程時,如果我們忽視了季節性模式的存在,我們也不會達到最簡約的模型。
後面會出一篇基於R語言的時間序列分析,基於SPSS的時間序列分析。
誰知道呢。
