00摘要

環島元素是智慧車比賽中較難處理的元素之一。比賽要求智慧車能檢測到環島並從入口駛入，在繞行約 270°後駛出環島，其中，能否高響應、高魯棒性地檢測環島是後續進出環島等步驟的基礎。本文根據計算機視覺中的多檢視幾何學證明了環島橢圓投影的存在，使用優化的最小二乘法擬合法並結合相關限制條件以識別環島。

^{▲ 主機板PCB}

01引言

環島元素是智慧車比賽中較難處理的元素之一，由於車身在行駛過程中存在不確定性，故難以保證穩定識別效果。如圖 1-1 與圖 1-2 所示。

^{▲ 圖 C-1 環島灰度圖}

^{▲ 圖 C-2 環島二值化圖}

本文分析了傳統電磁識別與攝像頭識別環島的優點和缺點，首先證明了環島橢圓投影的正確性，然後此基礎上提出了一種基於橢圓擬合的環島識別方法，通過拉格朗日運算元優化最小二乘誤差函數使其最小化，並將結果轉化為特徵向量的形式。最後通過模擬和實驗驗證了此環島識別方案的效能，並給出方案評價與可進一步研究的方向。

02現狀和方法

從資訊獲取的不同方式上來說，環島檢測方案可以分為攝像頭識別和電磁識別。

2.1 電磁識別

智慧車大賽道路中先佈置了通有 20kHz、100mA 交變電流的中心電磁引導線，頻率範圍 20k±1kHz，電流範圍 100±20mA。由於電磁引導線完全繞行與環島，在環島圓與賽道的交點處可等效為兩倍電磁場，故可在智慧車前支架設定

電感檢測裝置以檢測智慧車是否到達環島入口處，即點 B 處。若電磁測量值約為正常行駛時的兩倍，可置入環標誌位。

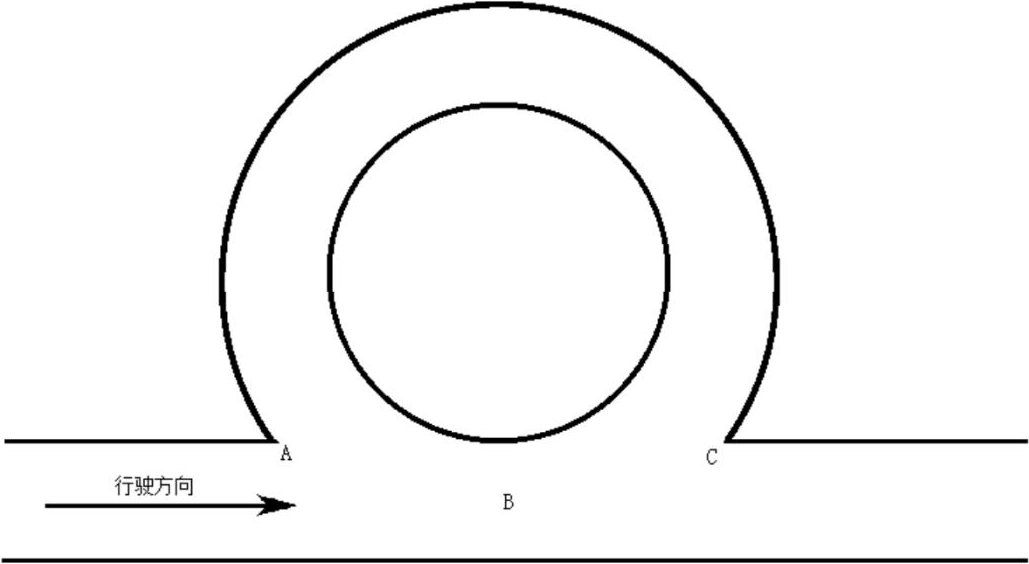
^{▲ 圖 C-3 環島示意圖}

此方案的缺點在於滯後檢測效應。當通過攝像頭正常尋跡時，由於車身到入環點才能檢測到環島，車輛在 A、B 點之間時，由於左側賽道缺失，智慧車會往左側偏移，隨後因掃描到環島內沿而校正回來，該過程使智慧車震盪，導致行駛

到 B 點處位置可能發生偏移，導致電感檢測失敗。此外，對於攝像頭為主要尋跡感測器的智慧車，多加電磁感測器使系統更加冗餘複雜。

2.2 攝像頭識別

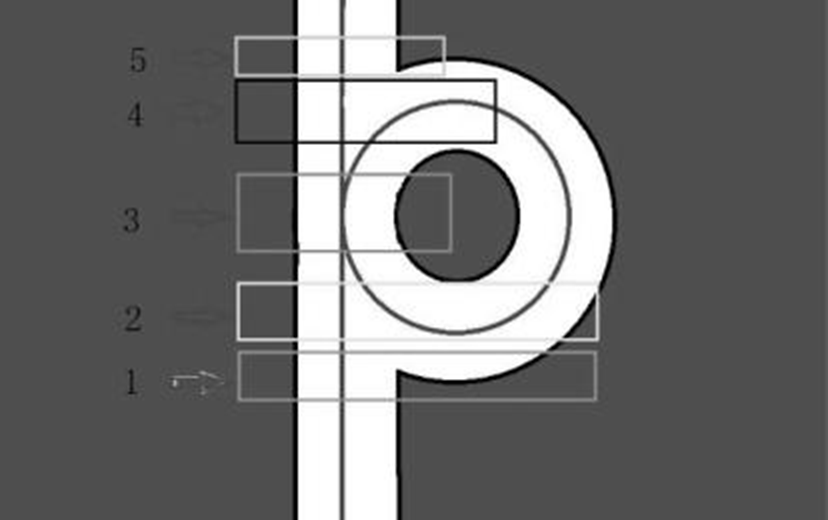
^{▲ 圖 C-4 流程式環島識別}

一種常規的，利用攝像頭進行環島入口識別的方法如下。

（1） 右側賽道突然變寬，左側賽道正常，標誌位置為 1。
（2） 右側賽道丟線，左側賽道正常，標誌位置為 2。
（3） 右側賽道由寬變窄，隨後又逐漸變寬，左側賽道不變，標誌位置為 3。
（4） 右側賽道再次丟線，標誌位置為 4。
（5） 若標誌位等於 4，則識別到環島。

該方案計算量較小，但仍然存在滯後檢測效應，智慧車會在區間 2 處小幅度右轉，影響後續過程的判斷過程。除此之外，該方案為流程化方案，若在判斷過程中有一個步驟意外出錯都無法正確判斷為環島入口，導致智慧車無法入環甚至衝出賽道。

03環島橢圓投影

對橢圓的投影進行建模，如下圖所示。將P平明的圓投影到H平面。設P平面的橢圓長半軸長度為A，短半軸的長度為B。P平面與H平面的夾角為$\alpha$。

取 $0^0<\alpha <90^0$。於P平面建立笛卡爾座標系XOY，橢圓長軸在X軸上，橢圓短軸在Y軸上，線段OO1的長度為L。可以平面P上的橢圓方程為：

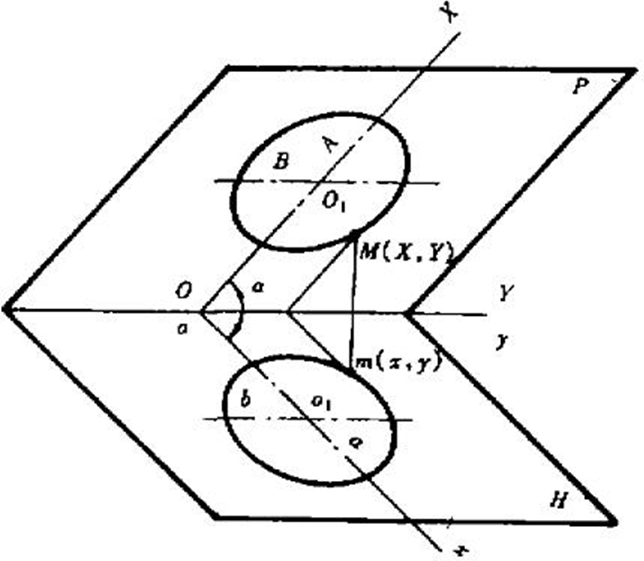
^{▲ 圖 C-5 橢圓對映圖}

一束平行光以$O_1{o}_1$的方向照燒，是P平面橢圓對映在H平面上，形成橢圓o1。

在平面H上建立笛卡爾座標系，oy與OY相重合，OX投影於ox，橢圓上一點M(X,Y)投影到m(x,y)，可知兩平面的座標系關係為：

聯立C-1與C-2，得：

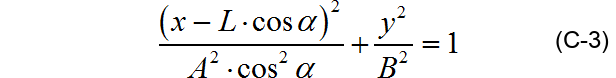
令$$m=A\cdot \cos \alpha ,n=B,p=L\cdot \cos \alpha$$

將C-3記作：

顯然，C-4為橢圓方程，即平面P上的橢圓經過平行光投影后仍然是橢圓。

特殊的，當平面P上的橢圓為圓時，有：$L=0,A=B=R$，則C-3為：

令$m^{\prime }=R\cdot \cos \alpha ,n^{\prime }=n$，平面H上的投影為：
$$\frac{x^2}{m^{\prime 2}}+\frac{y^2}{n^{\prime 2}}=1$$

顯然，當$\cos \alpha \ne 1$時，$m^{\prime }\ne n^{\prime }$，該解析式描述的為橢圓。

對於環島元素，設內環島邊緣為平面P上的圓。自然光線在P平面上的發生反射。由於物象距離較遠，反射光可近似為平行光。根據攝像機的真空成像模型，反射光在詳平面成像，即影象平面為H平面。因此，只需驗證內環島邊緣微橢圓即可。

^{▲ C 車模電機驅動PCB}

04最小二乘擬合

設橢圓一般方程為：
$$F\left(a,x\right)=a\cdot x=a{x}^2+bxy+c{y}^2+dx+ey+f=0$$

其中，
$$a={\left[a,b,c,d,e,f\right]}^T$$

$$x={\left[x^2,xy,y^2,x,y,1\right]}^T$$

對於一個待擬合的離散點集合，$X_i=\left(x,y\right)$，$F\left(a,X_i\right)$表示點Xi到橢圓$F\left(a,x\right)$的幾何距離。

最小二乘法的目標是求取使得李散掉的幾何距離最短的a，即最小化：
$$D_a=\sum _{i=1}^{N}F{\left(a,X_i\right)}^2$$

由於環島內邊緣投影為橢圓，而F(a,x)為廣義圓錐曲線一般表示式，需要表示為新增約束條件，以保證你和結果僅為橢圓。即：
$$4ac-b^2=1$$

為了表達方便，將前面方程吧粗歘在：

$$a^{T}Ca=1$$

其中：
$$c=\left[\begin{array}{c}\begin{array}{cccccc}0& 0& 2& 0& 0& 0\\ 0& -1& 0& 0& 0& 0\\ 2& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0\end{array}\end{array}\right]$$

故問題轉換為最小化誤差函數：
$$E={\Vert Da\Vert }^2$$

約束條件為：$$a^{T}Ca=1$$

其中矩陣：$$D=\left[X_1{X}_2\cdots X_N\right]$$

對於一個離散點：
$$X_i=\left[x^2,xy,y^2,x,y,1\right]$$

根據拉格朗日乘子法，求解$z=f\left(x,y\right)$在條件$\varphi \left(x,y\right)=1$下的極值，構造Lagrange函數：
$$L\left(x,y,\lambda \right)=f\left(x,y\right)+\lambda \varphi \left(x,y\right)$$

令：

求出x,y,lambda，可以得到：
$$2D^{T}Da-2\lambda Ca=0$$

令$D^{T}D=S$，則有：
$$Sa=\lambda Ca$$

由於S為實對稱矩陣，C為正定矩陣，故求解是為求解廣義特徵值問題。C正定，用$C^{-1}$做成上式，可以得到：
$$C^{-1}Sa=\lambda a$$

令$p=C^{-1}S$則：
$$pa=\lambda a$$

所以只需要求解上式的特徵向量a即可。根據數值分析冪法可求。

05限制條件

根據橢圓一般方程：

$$F\left(a,x\right)=a\cdot x=a{x}^2+bxy+c{y}^2+dx+ey+f=0$$

可的長半軸長度平方：
$$A^2=\frac{2\left(a{X}_c^2+c{Y}_c^2+b{X}_c{Y}_c-1\right)}{a+c+\sqrt{{\left(a-b\right)}^2+b^2}}$$

其中橢圓幾何中心：
$$X_c=\frac{be-2cd}{4ac-b^2},Y_c=\frac{bd-2ae}{4ac-b^2}$$

根據世紀環島的對映特點，限定如下識別條件：
（1）環島對映非長扁橢圓，約束為$0.2<\frac{A}{B}<5$。
（2）橢圓幾何中心在左上側，或者右上側，約束為$Y_C>\frac{H}{2}$，H為影象高度；
（3）以右環島為例，為保證提前識別，約束為右下側出現環島尖角。

06實驗結果

以圖C-2為計算範例，取內環島邊緣點獲取座標。

使用MATLAB 模擬得到橢圓方程為：

$$F\left(a,x\right)=0.00154x^2-0.019x\cdot y-0.156x$$$$+0.195\cdot y^2-3.390y+38.870$$

橢圓引數為：
$$A=30.537,B=5.099,X_c=150.053,Y_c=15.788$$

07總結和展望

本文提出了一種基於橢圓擬合的環島識別方法，相比於傳統的攝像頭識別與電感識別方法，該方法有以下特點。

（1） 無需流程式判斷，降低整體誤判斷概率。

（2） 具有遠前瞻特性，以免智慧車因丟線而誤轉向。

（3） 利用最小二乘的結果代替了程式迭代過程，提高了運算速度。

通過實驗分析研究表明，本文的方案有較快的運算速度、較強的棒性，不過仍有許多需要改進的地方，可在本文的基礎上進行以下深入研究。

（1） 尋找更好的求解特徵向量方法，進一步加快整體運算速度。

（2） 由於攝像機畫素較小，對於較小的橢圓難以正確擬合與判斷，可使用更高素質的攝像機。

（3） 由於車身位置變化，導致穩定尋找內環島邊緣區位置有一定困難，需要尋找更好的搜尋方法。

^{▲ 車模電機驅動PCB}

08參考文獻

[1] 彭慧敏. 平面斜截正圓錐截交線為橢圓時投影曲線分析. 西安建築科技大學學報: 自然科學版, 1998. 30(2): 第189-191頁.

[2] 莫章金. 橢圓的投影及其應用. 重慶建築高等專科學校學報, 1999. 9(2): 第28-31頁.

[3] Fitzgibbon, A., M. Pilu and R.B. Fisher, Direct least square fitting of ellipses. IEEE Transactions on pattern analysis and machine intelligence, 1999. 21(5): p. 476-480.

[4] Hal?r, R. and J. Flusser. Numerically stable direct least squares fitting of ellipses. 1998: Citeseer.

[5] 李成章, 黃玉民. 數學分析. 上北京: 科學出版, 1999.

[6] Trefethen, L.N. and D. Bau III, Numerical linear algebra. Vol. 50. 1997: Siam.

[7] 封建湖. 數值分析原理. 2001: 科學出版社.