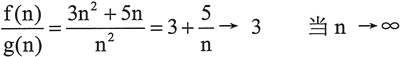演算法複雜度詳解
2020-07-16 10:04:41
【演算法 1】
sum = 0
k = 0 //陣列索引
While k < n do
sum = sum + a[k]
k = k + 1
EndWhile
現在來計算下面演算法 1 所需的步數。該演算法的組成包括:第 1 行和第 2 行中的兩個語句,它們各執行一次;第 4 行和第 5 行這兩個語句出現在迴圈中,每次回圈疊代時它們也各執行一次。前面介紹過,因為第 1 行和第 2 行的語句執行的是基本操作,所以可以將它們組合在一起,計為 1 個基本操作,在此可稱之為【操作 A】。
另外,因為迴圈中的兩個語句都是在常數時間內執行的,與 n 的大小無關,所以它們也是基本操作。由於迴圈體僅包含基本操作,演算法執行迴圈的單次疊代所需的時間量也是恆定的,不依賴於 n 的大小。這意味著可以將每個迴圈疊代計算為一個基本操作。這個操作可稱之為【操作 B】。
不管 n 有多大,操作 A 只執行一次。每次回圈疊代時,操作 B 執行一次。因為迴圈重複了 n 次,操作 B 也就被執行了 n 次。因此,該演算法操作執行的總次數是 1+n。例如,當 n=10 時,執行了 11 個操作;當 n=1000 時,執行了 1001 個操作;當 n= 10 000 時,執行的操作次數就是 10 001。請注意,隨著 n 變大,1 就變得微不足道,並且執行的操作次數大約為 n。因此可以說,該演算法所需的執行時間與 n 成正比,也就是與要處理的輸入集合的大小 n 呈正相關。
還可以通過另外一種方式來看待演算法 1,並確定它需要多少操作。要對陣列中的值求和,關鍵操作就是將每個值新增到累加求和的變數上,該操作發生在第 4 行,有多少次回圈疊代,就有多少次陣列值的相加。
因此,只需通過計算陣列元素的相加次數,也可以獲得相同的結果。事實證明,對於大多數演算法來說,只需要識別和計算一個或兩個對解決問題至關重要的基本操作即可。例如,在許多陣列搜尋和排序演算法中,只要計算陣列元素之間的比較次數就足夠了。
以上所討論的陣列求和演算法分析起來特別簡單,因為它對給定大小的所有輸入集執行相同的工作量。
但並不是所有演算法均如此。例如,本章前面介紹的線性搜尋演算法,它搜尋一個包含值的陣列,尋找匹配搜尋鍵碼的值。可以將關鍵字稱之為 X。演算法的輸入是陣列的大小 n 值和關鍵字 X 值。演算法的輸出是被找到的值所在的陣列位置的下標,或者,如果確定迴圈控制變數已經大於最後一個陣列元素的下標,則可以提示沒有找到。
形式上,該問題可以這樣描述:
- INPUT:大小為 n 的整數陣列 a[],以及整數 X。
- SIZE OF INPUT:輸入的陣列元素的個數 n。
- OUTPUT:一個整數 k,k 的取值範圍為 0≤k≤n-1,使得 a[k] = X 或 k = n。
以下顯示的是演算法 2,它使用了線性搜尋演算法來解決該問題。
【演算法 2】
k = 0
While k < n and a [k]≠X do
k = k + 1
End While
該演算法從一端開始,依次搜尋陣列。該演算法一旦遇到 X 就停止,但如果 X 不在陣列中,則會搜尋整個陣列。該演算法有可能在進行一次比較之後就會停止(X 在進行第一個陣列元素的匹配時即被發現),也有可能一直不停,直至它進行了 n 次比較(X 在最後一個陣列位置被發現或並不在陣列中)。實際上,該演算法可能會執行 m 次比較,其中 m 可以是從 1 到 n 的任何值。由此可見,該演算法對同樣大小的不同輸入可能需要執行不同次數的操作,在這種情況下,要衡量演算法的效率,往往需要對大小為 n 的輸入完成最大量的工作,這就是所謂的通過其最壞情況複雜度函數來衡量演算法。
演算法最壞複雜度
演算法的最壞情況複雜度函數(f(n))是它在大小為 n 的輸入上完成所需的最大工作量時執行的步驟數。它給出了演算法解決 n 個範例的問題所用的最長時間的指示,並且是在尋求效能保證時的一個很好的衡量指標。現在來確定本章前面介紹的二分搜尋的最壞情況下的複雜度。這個演算法用來在一個按升序排序的陣列中查詢專案 X。當在陣列中找不到 X 時,就會發生最壞的情況。在這種情況下,可以看到演算法將執行 L+1 個步驟,其中 L 是迴圈疊代的次數。
以下顯示的就是二分搜尋演算法的虛擬碼,它可以搜尋包含 n 個元素的陣列。
【演算法 3】
first = 0
last = n - 1 //n-1是陣列最後一個元素的下標
found = false
position = -1
While found is not true and first <= last
middle = (first + last) / 2
If a[middle] = X
found = true
position = middle
Else if a[middle] > X
last = middle - 1
Else
first = middle + 1
End If
End While
//當迴圈終止時,position 儲存的下標正是匹配X值的元素的下標
//如果未找到匹配值,則 position 儲存的值為 -1
該演算法由一些變數的初始化和一個迴圈組成。初始化需要的時間是恆定的,因此可以認為是 1 個基本操作。同樣,迴圈的每次疊代都是一個基本的步驟,因為增加陣列中的元素數量並不會增加單次迴圈所需的時間量。這意味著二分搜尋所需的步數為 L+1。現在,L 大約等於 log2n 的整數部分,即以 2 為底的 n 的對數。要理解這一點,請注意要搜尋的陣列的大小剛開始是 n,每次疊代之後,要搜尋的陣列的大小就只剩下大約一半。由於每個迴圈疊代至多執行兩次比較,所以二分搜尋需要執行的比較總次數就是 2log2n。於是可以將該查詢總結為:在最壞情況下,二分搜尋需要的時間與 log2n 成正比。
現在來看一看另外一個演算法,以確定其最壞情況下的複雜度。該演算法要解決的計算問題是將一組 n 個整數按升序排列:
- INPUT:n 個整數的陣列 a[]。
- SIZE OF INPUT:輸入的陣列元素的個數 n。
- OUTPUT:重新排序後的陣列 a[],使 a[0]≤a[1]≤...≤a[n-l]。
以下將使用的演算法是選擇排序演算法的修改版。這個版本掃描最大的元素(而不是最小的),並在每趟排序後將其移動到最後。
【演算法 4】
For (k = n-1; k> 1; k--)
// a[0..k]是餘下需要排序的部分
Determine position p of largest entry in a[0..k]
Swap a[p] with a[k]
End For
為了分析該演算法的複雜度,不妨從確定在對 n 個元素的陣列進行排序時需要進行比較的陣列元素數量開始。這些比較在步驟 3 中進行。步驟 3 顯然不是一個基本步驟,因為它需要的時間與 k 成比例,而k則會隨著迴圈的每次迭代而發生變化。為了更好地了解到底發生了什麼,不妨使用基本操作重新描述第 3 步:
INPUT:包含k + 1個元素的陣列a[0..k]。
SIZE OF INPUT:陣列元素的個數k + 1。
p = 0 //陣列未排序部分中最大值的位置
For (m = 1; m < k; m ++)
If a[m] > a[p] Then
p = m
End if
End For
現在可以看到,第 4?8 行的迴圈疊代了 k 次,而第 5 行在每次疊代時都進行了一次比較,因此這個演算法需要在陣列元素之間進行 k 次比較。現在返回到主排序演算法,可以發現,從第 4 行開始,到第 8 行結束的迴圈將進行 n-1 次疊代。對於範圍在 n-1 和 1 之間的 k 值,每個 k 值都會疊代一次。在第一次疊代時,k 等於 n-1,所以,正如上面 4 行到 8 行所分析的那樣,步驟 3 在陣列元素之間執行 n-1 次比較;在第二次疊代中,k 等於 n-2,所以步驟 3 執行 n-2 次比較。這樣一直持續到最後一次疊代時 k 等於 1,步驟 3 執行 1 次比較。
綜上所述,其結果計算如下:
- k = n-1:步驟 3 執行 n-1 次比較;
- k = n-2:步驟 3 執行 n-2 次比較;
- k = 1:步驟 3 執行 1 次比較。
歸納起來,於是就可以這樣說:對於從 n-1 到 1 的每個 k 值,在第 k 次疊代中,第 3 行上的步驟將執行 k 次比較。
因此,這個簡單的排序演算法進行比較的總次數就可以由以下表示式獲得。
1+2 + 3 +...+(n-1)=(n-1)n/2
如果 n 值比較大,那麼這個表示式的結果非常接近於 n2/2。所以可以得出結論說:在最壞的情況下,選擇排序所需的時間與 n2 成正比。平均情況下的複雜度
當然,最壞情況下的複雜度,並不能很準確地說明演算法在實際情況下的表現如何,因為在實際環境中最壞情況的出現可能是很少見的。一般情況下,程式設計師更感興趣的是確定典型或平均情況下的複雜度。當我們知道實際環境中可能發生的不同輸入的相對頻率時,即可使用平均情況複雜度函數。平均情況複雜度函數使用這些頻率來形成在每個輸入上執行的步驟數的加權平均值。不幸的是,雖然它可以很好地衡量演算法的預期效能,但是可能很難獲得對輸入頻率的精確估計。
漸近複雜度與大O表示法
要比較解決問題的兩種演算法 F 和 G,可以通過比較它們的複雜度函數來進行。更具體地來說,如果 f(n) 和 g(n) 是兩種演算法的複雜度函數,則可以通過觀察當 n 變大時,f(n)/g(n) 比例值的變化來比較這兩種演算法。如果比例值趨向某個極限,那麼它就很好理解。現在來看幾個具體的範例,當然,還是需要假設 f(n)≥1、g(n)≥1 並且所有 (n)≥1。f(n) = 3n2 + 5n 並且 g(n) = n2。在這種情況下: