1.線性系統理論是控制理論中的基礎內容，主要是研究線性系統狀態的運動規律和改變這種運動規律的可能性和方法，以建立和揭示系統結構、引數、行為和效能間的確定的和定量的關係。
2.基本的研究方法和步驟：
①建立描述物理系統狀態的數學模型：通過實驗、物理定律和數學方程等來得到模型。一般由微分方程、差分方程、偏分方程或代數方程等構成。
②基於模型的系統分析：定性、定量的分析可控可觀、穩定性等。
③系統設計：通過設計控制器或改變控制律來改善系統的效能指標。
④系統執行：→（3/2/1）
3.控制系統的數學描述：
輸入/輸出描述：描述的是系統的外部特性。
狀態空間描述：系統內外部特性，是一種全面的描述方法。由於獲得了系統的全面資訊，故可設計出效能更好的系統。但在許多情況下，實現系統的狀態空間描述是困難的。

一、系統輸入-輸出描述

1.輸入/輸出描述

不知道系統內部結構資訊，唯一可測量的量是系統的輸入輸出訊號，通過各類輸入，獲取輸出，獲得特性。當系統輸入輸出都只有一個時，為單變數系統；輸入或輸出多於一個時，為多變數系統。

2.初始鬆弛

如果一個只有輸入和輸出可測量的系統，即輸入—輸出系統，對相同的輸入有不同的輸出，那麼對其描述就沒有意義。初始鬆弛實際上就是，在經典控制中，初始條件為零這樣一個假設。
例如簡單的二階系統：
$${\ddot{y}}_c+2{\dot{y}}_c+y_c=u\begin{array}{cc}& \end{array}\left(t\ge t_0=0\right)$$
從微分方程的解可知，其定解條件是有確定的初始條件，如果初始條件不能確定，那麼輸出就不能由輸入$u$唯一確定，
$${\dot{y}}_c\left(0\right),y_c\left(0\right)$$
如若假定系統的初始條件為零，從能量角度看，表示系統從$-\infty$到0時間段內儲能為零。
$$\begin{gathered} y_c\left(t\right)={\int }_0^{t}h\left(t-\tau \right)u\left(\tau \right)d\tau \\ {y}_c=Hu=h\ast u \end{gathered}$$

對於一個任意的物理系統，假定其在$-\infty$處的儲能為零，或者說，在$-\infty$處於鬆弛狀態或靜止狀態總是合理的。定義：$-\infty$時鬆弛或靜止的系統為初始鬆弛系統，簡稱鬆弛系統。
上式中$H$是一個運算元，在複數域上，傳遞函數就是將輸入對映為輸出的運算元，在實施域上，是折積運算$h\left(t\right)$是脈衝響應函數。

3.線性系統

1）線性系統定義：對於一個鬆弛系統為線性系統，當且僅當對於任何輸入$u_1$和$u_2$，以及任意實數或複數${\alpha }_1$和${\alpha }_1$，有
$$H({\alpha }_1{u}_1+{\alpha }_2{u}_2)={\alpha }_{1}H{u}_1+{\alpha }_{2}H{u}_2$$
實際上就是疊加原理=齊次性和可加性，滿足疊加原理是線性系統的唯一判據。對於拉普拉斯運算元就是線性系統。
2）線性鬆弛系統的脈衝響應：
①首先引入$\delta$函數或脈衝函數的概念：
對於一段脈衝：
$${\delta }_{\Delta }(t-t_1)=\{\begin{array}{cc}0& t<t_1\\ \frac{1}{\Delta }& t_1\le t<t_1+\Delta \\ 0& t\ge t_1+\Delta \end{array}$$
其極限形式就是脈衝函數，簡稱$\delta$函數：
$$\delta \left(t-t_1\right)=\underset{\Delta \to 0}{\lim }{\delta }_{\Delta }\left(t-t_1\right)$$
②$\delta$函數的取樣性：對於在$t_1$連續的任意函數
$${\int }_{-\infty }^{+\infty }f\left(t\right)\delta \left(t-t_1\right)dt=f\left(t_1\right)$$
故可以用${\delta }_{\Delta }\left(t-t_1\right)$近似表示訊號：
$$u\left(t\right)\approx \sum _n{\delta }_{\Delta }\left(t-t_n\right)\left[u\left(t_n\right)\Delta \right]$$
③進一步的線性系統的脈衝響應函數就可以表示為：
$$\begin{array}{rl}& y=Hu\approx Hu\left(t\right)\\ & =\sum _n\left[H{\delta }_{\Delta }\left(t-t_n\right)\right]\left[u\left(t_n\right)\Delta \right]\end{array}$$
取極限，就可以表示成積分的形式，
$$y={\int }_{-\infty }^{+\infty }H\delta \left(t-\tau \right)u\left(\tau \right)d\tau$$
其中$H\delta \left(t-\tau \right)$就是脈衝響應函數，其意義是在$\tau$時刻，對線性系統施加一個脈衝響應函數，從而得到系統輸出，所有也可以表示為雙變數的形式：
$$H\delta \left(t-\tau \right)=g\left(\xi ,\tau \right)$$

4.因果性

1）定義：
若系統在時刻t 的輸出只取決於時刻 t 和 在 t 之前的輸入，而不取決於 t 之後的輸入則稱系統具因果性。
任何實際的物理系統都是具有因果性的。通俗地說，任何實際物理過程，結果總不會在引起這種結果的原因發生之前產生，即未來的輸入（原因）對過去和現在的輸出（結果）無影響。
2）截斷運算元表示系統的因果性：
$$\forall T\begin{array}{cc}& \end{array}{P}_T\left(Hu\right)=P_T\left(H{P}_{T}u\right)$$

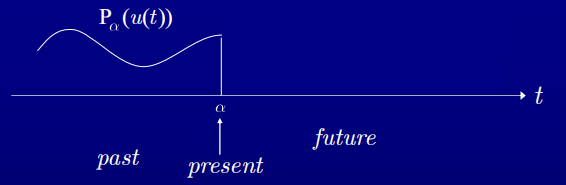
左邊輸入比右邊多了的T之後的一段，而輸出在兩邊是一樣的，這說明的T之後的輸入對輸出無影響。

5.$t_0$時刻的鬆弛性

1）定義：系統在時刻$t_0$稱為鬆弛的，當且僅當$t\ge t_0$時的輸出y僅唯一地由$t\ge t_0$時的輸入u所決定，即$y_{\left[t_0,+\infty \right)}$僅唯一地由$u_{\left[t_0,+\infty \right)}$決定。
若已知系統在 t0時鬆弛，則輸入/輸出關係可以寫成
$$y_{\left[t_0,+\infty \right)}=H{u}_{\left[t_0,+\infty \right)}$$
2)充分條件：若一個線性系統滿足$u_{\left(-\infty ,t_0\right)}$，則系統必定在t0時刻鬆弛。
3）充要條件：

6.時不變性

1）定義：一個鬆弛的時不變線性系統的特性：輸入訊號延遲$\alpha$ 秒，其響應也恰好延遲$\alpha$秒，且波形不變，即系統特性不隨時間而變化。
位移運算元：經$Q_{\alpha }$作用後的輸出等於延遲了$\alpha$秒的輸入。
定義：鬆弛系統為時不變系統，當且僅當對於任何輸入u和任何實數$\alpha$，有
$$Q_{\alpha }y=Q_{\alpha }Hu=H{Q}_{\alpha }u$$
2）時不變系統的脈衝響應函數
根據時不變的特性可以推導：
$$\begin{array}{rl}& g\left(t,\tau \right)=g\left(t-\tau ,0\right)\\ & =g\left(t+\alpha ,\tau +\alpha \right)\\ & =g\left(t-\tau \right)\end{array}$$
對時不變系統來說，脈衝響應僅取決於觀測時刻 t 與脈衝作用時刻$\tau$的差。

7.傳遞函數陣和極點多項式

1）已知系統脈衝響應矩陣，對個元素直接進行Laplace變換得到傳遞函數陣。
2）正則性定義：$G\left(\infty \right)$是一個非零的常數矩陣，有理傳遞矩陣G(s)稱為是正則的；$G\left(\infty \right)=0$，G(s)稱為是嚴格正則的。
3）傳遞函數陣的極點：G(s)所有不恆為零的各階子式的首一最小公分母稱為G(s)的極點多項式。極點多項式的根稱為G(s)的極點。
4）傳遞函數陣的零點：G(s)的所有r 階子式，在其分母取G(s)的極點多項式時，其分子多項式的首一最大公因式稱為G(s)的零點多項式。零點多項式的根稱為G(s)的零點。

二、系統的狀態變數描述

1.什麼是狀態變數

1）能和$u_{\left[t_0,+\infty \right)}$一起唯一地確定系統在所有$t\ge t_0$時的行為的系統t0時刻的資訊量,稱為系統在t0時刻的狀態。行為包括輸出和資訊量本身的更新，隨時間$t\ge t_0$不斷更新的資訊量稱為狀態變數，以狀態變數構成的向量稱為狀態向量。
2）特點：
第一，狀態變數的不唯一性，一般取有物理意義的量；
第二，狀態變數的數目等於且僅僅等於系統中包含獨立貯能元件的數目；
第三，狀態變數的數目的可以是有限個，也可以是無限多個；（例如延遲系統無限個值作為初始狀態）
第四，狀態向量取值的實向量空間，稱為狀態空間。

2.線性時不變動態方程

動態方程：系統的動態方程是由狀態方程和輸出方程組成的，n維線性時不變動態方程一般形式為：
$$\begin{array}{rl}& \dot{\mathbf{x}}=\mathbf{A}\mathbf{x}+\mathbf{B}\mathbf{u}\\ & \mathbf{y}=\mathbf{C}\mathbf{x}+\mathbf{D}\mathbf{u}\end{array}$$

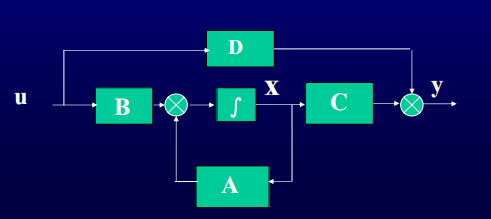
3.時不變系統的傳遞函數矩陣

動態方程進行Laplace變換可得，
$$\begin{array}{rl}& y\left(s\right)=\left[\mathbf{C}{(s\mathbf{I}-\mathbf{A})}^{-1}\mathbf{B}+\mathbf{D}\right]u\left(s\right)=\mathbf{G}\left(s\right)u\left(s\right)\\ & \mathbf{G}\left(s\right)=\mathbf{C}{(s\mathbf{I}-\mathbf{A})}^{-1}\mathbf{B}+\mathbf{D}\end{array}$$

4.預解矩陣${(s\mathbf{I}-\mathbf{A})}^{-1}$