C++ uniform_real_distribution連續均勻分布類別範本用法詳解
2020-07-16 10:04:27
std::uniform_real_distribution<> values {0.0, 10.0};
std::random_device rd; // Non-de terrains tic seed source
std::default_random_engine rng {rd()}; // Create random number generator for(size_t i {}; i<8; ++i)
std::cout << std::fixed << std::setprecision(2)<< values (rng) <<" ";
// 8.37 6.72 6.41 6.08 6.89 6.10 9.75 4.07
生成和使用 uniform_real_distribution 函數物件的方式和 uniform_int_distribution 有密切的相似之處。可以將一個亂數生成器物件作為引數值給分布函數物件來獲取一個隨機值。可以通過呼叫物件的成員函數 pamm() 來獲取和設定範圍的界限。除了返回分布界限的成員函數 min() 和 max(),uniform_real_distribution 物件也有成員函數 a() 和 b()。注意,連續分布的範圍是半開放的,分布物件返回值的範圍不包括上邊界。現實世界中,能夠應用均勻連續分布的變數是很少的。例如,和天氣相關的引數的測量中,範圍值並不是等可能性的。當我們看手錶時,秒針的位置可能是一個均勻分布,但這沒有什麼用,這可能是真正的範例。均勻連續分布被用在應用於金融業的蒙特卡羅方法中,也被用到了工程和科學中。將它們放到一個使用連續均分分布或 π 的值程式。
使用連續均勻分布
你知道可以用一根木棍來確定 π 的值嗎?當然,並不是讓你用木棍來烕脅一個數學家,從而讓他告訴你 π 的值,而是可以扔任意一根直的物品一鉛筆甚至法拉克福香腸都可以。必須是一塊光禿禿的帶有地板的地面,並且扔的物品也必須是直的,它的長度必須小於地板的長度。過程很簡單一只需要數扔木棍的次數,以及木棍落地時,它穿越地板邊緣的次數。為了得到一個不錯的結果,需要將棍子拋擲一定的次數。當然,這會花費一些時間,並且還有點乏味,並不是說有多累。在幾組均勻分布的幫助下,我們可以通過電腦來模擬拋擲並計算處 π 的值。圖 1 展示了木棍在地面上的隨機位置以及它和地板的關係。為了解釋發生了什麼,需要用到一點數學知識,但並不難。
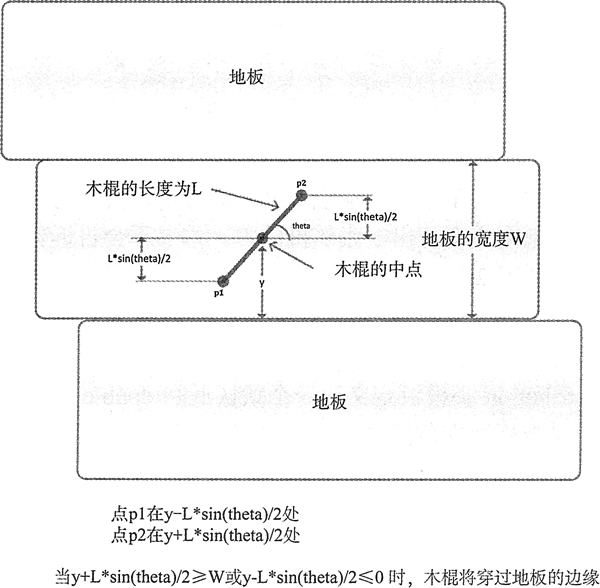
圖 1 地板上的木棍