C語言求親密數（詳解版）

問題描述

如果整數A的全部因子（包括1，不包括A本身）之和等於B；且整數B的全部因子（包括1，不包括B本身）之和等於A，則將整數A和B稱為親密數。求3000以內的全部親密數。

問題分析

根據問題描述，該問題可以轉化為：給定整數A，判斷A是否有親密數。

為解決該問題，首先定義變數a，並為其賦初值為某個整數。則按照親密數定義，要判斷a中存放的整數是否有親密數，只要計算出該整數的全部因子的累加和，並將該累加和存放到另一個變數b中，此時b中存放的也是一個整數。再計算b中存放整數的全部因子的累加和，將該累加和存放到變數n中。

若n等於a則可判定變數a和b中所存放的整數是親密數。

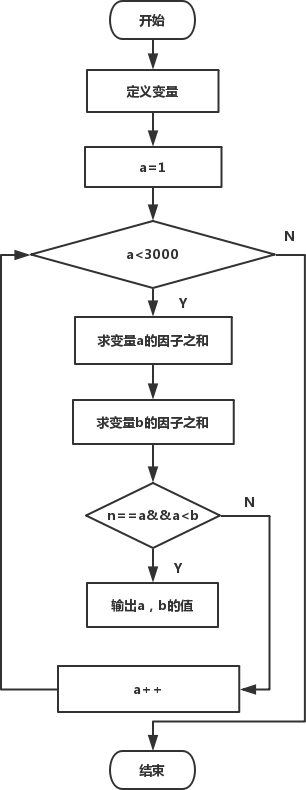
演算法設計

計算數A的各因子的演算法：用A依次對i（i的範圍可以是1?A-1、1?（A/2-1）中之一） 進行模（“%”，在程式設計過程中一定注意求模符號兩邊參加運算的資料必須為整數）運算，若模運算結果等於0，則i為A的一個因子加；否則i就不是A的因子。將所求得的因子累到變數B。

接下來求變數B的因子：演算法同上，將B的因子之和累加到變數n。根據親密數的定義判斷變數n是否等於變數A(if(n==a))，若相等，則A和B是一對親密數，反之則不是。

程式流程圖：


下面是完整的程式碼：

#include<stdio.h>
int main()
{
    int a, i, b, n;
    printf("There are following friendly--numbers pair smaller than 3000:n");
    for( a=1; a<3000; a++ )  /*窮舉3000以內的全部整數*/
    {
        for( b=0, i=1; i<=a/2; i++)  /*計算數a的各因子，各因子之和存放於b*/
            if(!(a%i))
                b+=i;
        for( n=0, i=1; i<=b/2; i++ )  /*計算b的各因子，各因子之和存於n*/
            if(!(b%i))
                n+=i;
        if(n==a && a<b)  /*使每對親密數只輸出一次*/
            printf("%4d--%4d    ", a, b);  /*若n=a，則a和b是一對親密數，輸出*/
    }
   
    return 0;
}

執行結果：
There are following friendly--numbers pair smaller than 3000:
220-- 284    1184--1210    2620--2924

知識點補充

對於這類多次將某些值儲存到一個變數中時，一定要注意變數賦初值的位置。