C語言求自守數(詳解版)
2020-07-16 10:04:27
52 = 25 252 = 625 762 = 5776 93762 = 87909376
求100000以內的自守數。問題分析
根據自守數的定義,求解本題的關鍵是知道當前所求自然數的位數,以及該數平方的尾數與被乘數、乘數之間的關係。演算法設計
若採用“求出一個數的平方後再擷取最後相應位數”的方法顯然是不可取的,因為計算機無法表示過大的整數。分析手工方式下整數平方(乘法)的計算過程,以376為例:

本問題所關心的是積的最後三位。分析產生積的後三位的過程可以看出,在每一次的部分積中,並不是它的每一位都會對積的後三位產生影響。總結規律可以得到:在三位數乘法中,對積的後三位產生影響的部分積分別為:
- 第一個部分積中:被乘數最後三位×乘數的倒數第一位。
- 第二個部分積中:被乘數最後二位×乘數的倒數第二位。
- 第三個部分積中:被乘數最後一位×乘數的倒數第三位。
將以上的部分積的後三位求和後,擷取後三位就是三位數乘積的後三位,這樣的規律可以推廣到同樣問題的不同位數乘積中。
分離給定數中的最後幾位
從一個兩位數(存在變數n中)開始分析,分離最低位個位n%10;對於三位數n,分離最後兩位n%100;對於四位數n,分離最後三位n%1000;...,由此可見,若分離出最後x位,只需要用原數對 10x 求餘。從第3部分所舉例子可以看出,對於第二個部分積“2632”來說其實應是“26320”, 因為對於乘數中的倒數第二位“7”來說,因其在十位,對應的權值為10,第二個部分積實質上為:376X70=26320。故求部分積的程式段為:
int main ()
{
//...
while(k>0)
{
mul=( mul + ( number%(k*10) )*( number%b - nxuober%(b/10) ) )%a;
/* (部分積+擷取被乘數的後N位*擷取乘數的第M位),%a再擷取部分積*/
k /= 10; /*k為擷取被乘數時的係數*/
b *= 10;
}
//...
return 0;
}
對於整個迴圈來說,變數k是由number的位數確定擷取數位進行乘法時的係數。第1次執行迴圈體時,被乘數的所有位數都影響到平方的尾數,因此第1個部分積=被乘數*乘數的最後一位,將部分積累加到變數mul上,再對a取餘擷取相應的尾數位數;第2次執行迴圈體,影響平方尾數的是被乘數中除了最高位之外的數(所以k先除以10再參加運算),第2個部分積=被乘數*乘數的倒數第二位,( number%b - number%(b/l0) )用來求乘數中影響平方尾數的對應位上的數;第3次、第4次執行迴圈體的過程同上。程式流程圖:
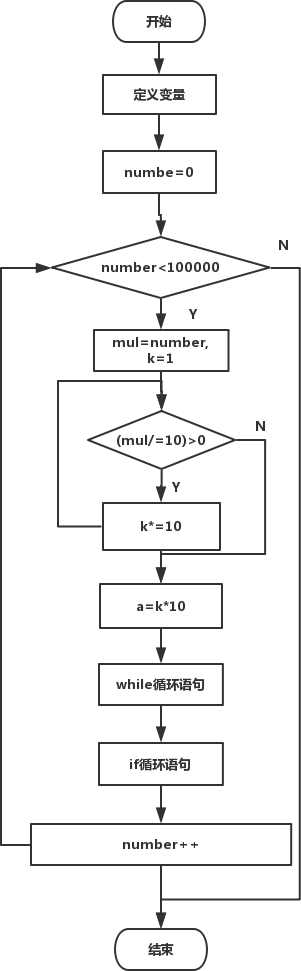
下面是完整的程式碼:
#include<stdio.h>
int main()
{
long mul, number, k, a, b;
printf("It exists following automorphic nmbers small than 100000:n");
for( number=0; number<100000; number++ )
{
for( mul=number, k=1; (mul/=10)>0; k*=10 );
/*由number的位數確定擷取數位進行乘法時的係數k*/
a = k * 10; /*a為擷取部分積時的係數*/
mul = 0; /*積的最後n位*/
b = 10; /*b為擷取乘數相應位時的係數*/
while(k>0)
{
mul=( mul + ( number%(k*10) )*( number%b - number%(b/10) ) )%a;
/*(部分積+擷取被乘數的後N位*擷取乘數的第M位),%a再擷取部分積*/
k /= 10; /*k為擷取被乘數時的係數*/
b *= 10;
}
if(number == mul) /*判定若為自守數則輸出*/
printf("%ld ", number);
}
printf("n");
return 0;
}
執行結果:It exists following automorphic nmbers small than 100000:
0 1 5 6 25 76 376 625 9376 90625