在二元搜尋樹中刪除元素

函式delete()用於從二元搜尋樹中刪除指定的節點。 但是，不能違反二元搜尋樹的屬性。 從二元搜尋樹中刪除節點有三種情況。

1. 要刪除的節點是葉節點

這是最簡單的情況，在這種情況下，用NULL替換葉節點並簡單地釋放分配的空間。
在下圖中，假設要刪除節點85，因為此節點是葉節點，因此節點將被替換為NULL並且將釋放分配的空間。

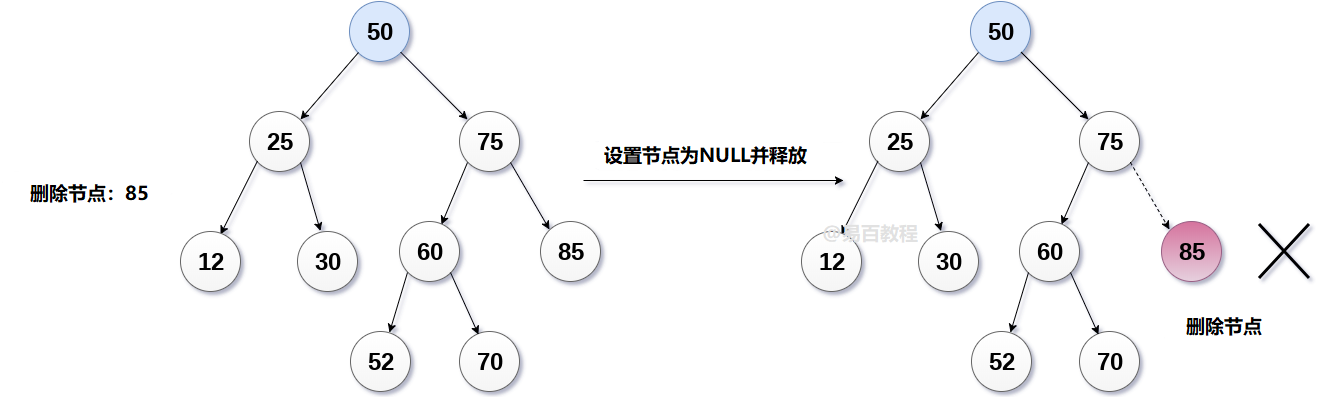
2. 要刪除的節點只有一個子節點

在這種情況下，將節點替換為其子節點並刪除子節點，該子節點現在包含要刪除的值。 只需將其替換為NULL並釋放分配的空間即可。

在下圖中，將刪除節點12。 它只有一個子節點。 該節點將被其子節點替換，並且將簡單地刪除替換的節點12(現在是葉節點)。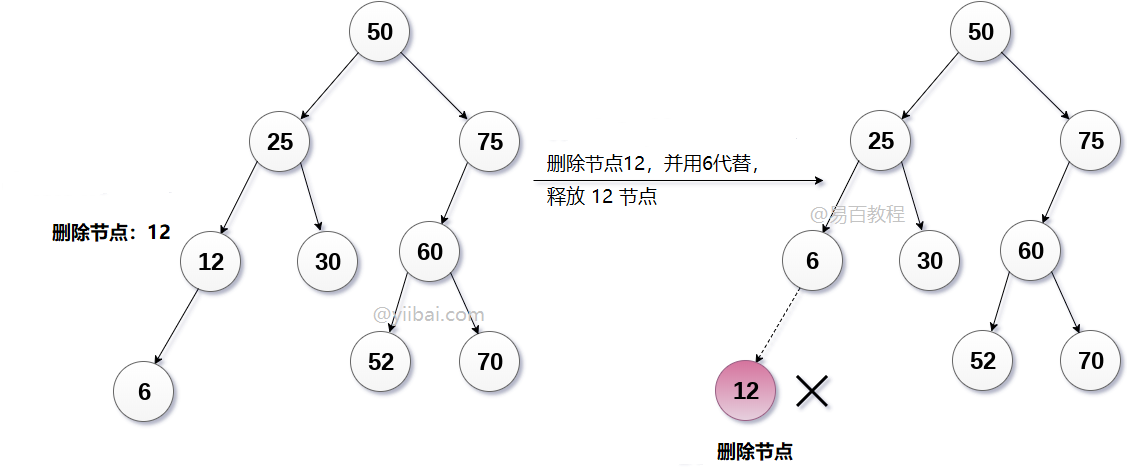

3. 要刪除的節點有兩個子節點

與上面的兩種情況相比，這種情況有點複雜。 但是，要刪除的節點被遞回地替換為其有序後繼或前導，直到將節點值(要刪除)放置在樹的葉子上。 在該過程之後，用NULL替換節點並釋放分配的空間。

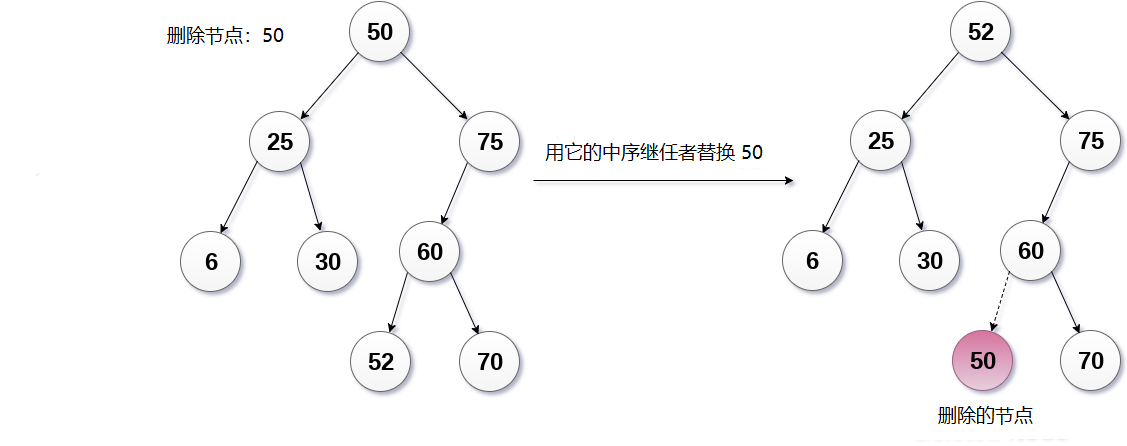
在下面的影象中，要刪除節點50，它是樹的根節點。 下面給出的樹的有序遍歷。

6, 25, 30, 50, 52, 60, 70, 75

用它的中序繼任者替換50。現在，50將被移動到樹的葉子，之後將被刪除。

演算法

Delete (TREE, ITEM)

第1步 : IF TREE = NULL
      提示： "item not found in the tree" ELSE IF ITEM < TREE -> DATA
     Delete(TREE->LEFT, ITEM)
     ELSE IF ITEM > TREE -> DATA
   Delete(TREE -> RIGHT, ITEM)
     ELSE IF TREE -> LEFT AND TREE -> RIGHT
     SET TEMP = findLargestNode(TREE -> LEFT)
     SET TREE -> DATA = TEMP -> DATA
      Delete(TREE -> LEFT, TEMP -> DATA)
     ELSE
   SET TEMP = TREE
   IF TREE -> LEFT = NULL AND TREE -> RIGHT = NULL
      SET TREE = NULL
     ELSE IF TREE -> LEFT != NULL
     SET TREE = TREE -> LEFT
     ELSE
    SET TREE = TREE -> RIGHT
     [IF結束]
  FREE TEMP
[IF結束]
第2步: 結束

使用C語言實現刪除二元搜尋樹的節點，如下 -

void deletion(Node*& root, int item)  
{  
    Node* parent = NULL;  
    Node* cur = root;  

    search(cur, item, parent);  
    if (cur == NULL)  
        return;  

    if (cur->left == NULL && cur->right == NULL)  
    {  
        if (cur != root)  
        {  
            if (parent->left == cur)  
                parent->left = NULL;  
            else  
                parent->right = NULL;  
        }  
        else  
            root = NULL;  

        free(cur);       
    }  
    else if (cur->left && cur->right)  
    {  
        Node* succ  = findMinimum(cur- >right);  

        int val = succ->data;  

        deletion(root, succ->data);  

        cur->data = val;  
    }  

    else  
    {  
        Node* child = (cur->left)? Cur- >left: cur->right;  

        if (cur != root)  
        {  
            if (cur == parent->left)  
                parent->left = child;  
            else  
                parent->right = child;  
        }  

        else  
            root = child;  
        free(cur);  
    }  
}  

Node* findMinimum(Node* cur)  
{  
    while(cur->left != NULL) {  
        cur = cur->left;  
    }  
    return cur;  
}