Kruskal演算法
2019-10-16 22:02:18
Kruskal演算法用於查詢連線加權圖的最小生成樹。該演算法的主要目標是通過使用哪個來找到邊的子集,可以遍歷圖的每個頂點。Kruskal演算法遵循貪婪的方法,在每個階段找到最佳解決方案,而不是專注於全域性最優。
Kruskal演算法如下。
第1步:建立一個森林,使每個圖形都是一個單獨的樹。
第2步:建立包含圖表所有邊緣的優先順序佇列Q。
第3步:重複第4步和第5步,而Q不為空。
第4步:從Q中刪除邊
第5步:如果在步驟4中獲得的邊連線兩個不同的樹,則將其新增到森林中(用於將兩個樹組合成一個樹)。
其他
丟棄邊
第6步:結束
範例:
將Kruskal演算法應用於如下圖表。
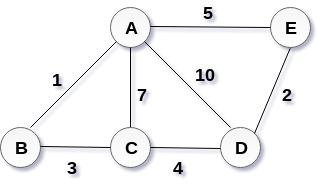
解決方案:
邊的權重如下:
| 邊 | AE | AD | AC | AB | BC | CD | DE |
|---|---|---|---|---|---|---|---|
| 權重 | 5 | 10 | 7 | 1 | 3 | 4 | 2 |
根據權重對邊進行排序。
| 邊 | AB | DE | BC | CD | AE | AC | AD |
|---|---|---|---|---|---|---|---|
| 權重 | 1 | 2 | 3 | 4 | 5 | 7 | 10 |
開始構建樹,將AB新增到MST;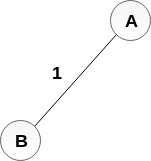
將DE新增到MST;

將BC新增到MST;
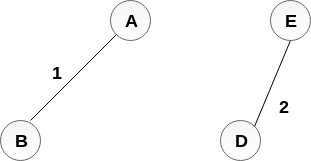
下一步是新增AE,但不能新增它,因為它會導致迴圈。
要新增的下一個邊是AC,但不能新增,因為它會導致迴圈。
要新增的下一個邊是AD,但無法新增,因為它將包含一個迴圈。
因此,最終的MST是步驟4中所示的MST。
MST的成本 = 1 + 2 + 3 + 4 = 10。
使用C++實現上面演算法,程式碼如下所示 -
#include <iostream>
#include <vector>
#include <utility>
#include <algorithm>
using namespace std;
const int MAX = 1e4 + 5;
int id[MAX], nodes, edges;
pair <long long, pair<int, int> > p[MAX];
void init()
{
for(int i = 0;i < MAX;++i)
id[i] = i;
}
int root(int x)
{
while(id[x] != x)
{
id[x] = id[id[x]];
x = id[x];
}
return x;
}
void union1(int x, int y)
{
int p = root(x);
int q = root(y);
id[p] = id[q];
}
long long kruskal(pair<long long, pair<int, int> > p[])
{
int x, y;
long long cost, minimumCost = 0;
for(int i = 0;i < edges;++i)
{
x = p[i].second.first;
y = p[i].second.second;
cost = p[i].first;
if(root(x) != root(y))
{
minimumCost += cost;
union1(x, y);
}
}
return minimumCost;
}
int main()
{
int x, y;
long long weight, cost, minimumCost;
init();
cout <<"Enter Nodes and edges";
cin >> nodes >> edges;
for(int i = 0;i < edges;++i)
{
cout<<"Enter the value of X, Y and edges";
cin >> x >> y >> weight;
p[i] = make_pair(weight, make_pair(x, y));
}
sort(p, p + edges);
minimumCost = kruskal(p);
cout <<"Minimum cost is "<< minimumCost << endl;
return 0;
}
執行上面範例程式碼,得到以下結果:
Enter Nodes and edges5
5
Enter the value of X, Y and edges5
4
3
Enter the value of X, Y and edges2
3
1
Enter the value of X, Y and edges1
2
3
Enter the value of X, Y and edges5
4
3
Enter the value of X, Y and edges23
3
4
Minimum cost is 11