P2014 [CTSC1997]選課(樹形dp)
選課
Description
大學裏實行學分。每門課程都有一定的學分,學生只要選修了這門課並考覈通過就能獲得相應的學分。學生最後的學分是他選修的各門課的學分的總和。
每個學生都要選擇規定數量的課程。其中有些課程可以直接選修,有些課程需要一定的基礎知識,必須在選了其它的一些課程的基礎上才能 纔能選修。例如,《數據結構》必須在選修了《高階語言程式設計》之後才能 纔能選修。我們稱《高階語言程式設計》是《數據結構》的先修課。每門課的直接先修課最多隻有一門。兩門課也可能存在相同的先修課。爲便於表述每門課都有一個課號,課號依次爲1,2,3,……。下面 下麪舉例說明
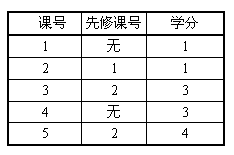
上例中1是2的先修課,即如果要選修2,則1必定已被選過。同樣,如果要選修3,那麼1和2都一定已被選修過。
學生不可能學完大學所開設的所有課程,因此必須在入學時選定自己要學的課程。每個學生可選課程的總數是給定的。現在請你找出一種選課方案,使得你能得到學分最多,並且必須滿足先修課優先的原則。假定課程之間不存在時間上的衝突。
Input
輸入檔案的第一行包括兩個正整數M、N(中間用一個空格隔開)其中M表示待選課程總數(1≤M≤1000),N表示學生可以選的課程總數(1≤N≤M)。
以下M行每行代表一門課,課號依次爲1,2……M。每行有兩個數(用一個空格隔開),第一個數爲這門課的先修課的課號(若不存在先修課則該項爲0),第二個數爲這門課的學分。學分是不超過10的正整數。
Output
輸出檔案第一行只有一個數,即實際所選課程的學分總數。以下N行每行有一個數,表示學生所選課程的課號。
Sample Input
7 4
2 2
0 1
0 4
2 1
7 1
7 6
2 2
Sample Output
13
解題思路
這題和P2015 二叉蘋果樹(樹形dp) 差不多
這題不是一棵2叉樹,而是一棵多叉樹
具體方法就是把第一個兒子放在父節點的左子樹,其他兒子放在其兒子的右子樹上。 定義 f[x,y] 表示根節點x,選y門課,可以得到的最優值。 轉移方程有
F[x,y]=max{F[x.Lson,k-1]+F[x.Rson,y-k]+w[x]} 0<=k<=y
AC程式碼
#include<iostream>
#include<cstdio>
using namespace std;
int n,m,b[305],a[305][305],f[305][305],tree[305][305];
void dp(int x)//dp
{
b[x]=1;//標記
for(int i=1;i<=tree[x][0];i++)//tree[][0]是他的兒子個數,tree[][1-n]是他的兒子
{
if(b[tree[x][i]])continue;//判斷是否標記過,免得形成環
dp(tree[x][i]);//遞回
for(int j=m;j>=0;j--)//dp
for(int k=j-1;k>=0;k--)
f[x][j]=max(f[x][j],f[tree[x][i]][k]+f[x][j-k-1]+a[x][tree[x][i]]);//狀態轉移
}
}
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
{
int x, y;
scanf("%d%d",&x,&y);//輸入
a[x][i]=y;
tree[x][++tree[x][0]]=i;
}
dp(0);//dp
printf("%d",f[0][m]);//輸出
}