title: 慕課網-演算法與數據結構—學習總結
date: 2020-08-12 16:21:41
tags: LearnNotes

慕課網-演算法與數據結構-學習總結

第一章引言

課程原始碼play-with-Algorithms

第二章排序基礎

排序的穩定性
排序後是否改變原序列鍵值相同的序列的先後先後關係
內排序與外排序
外排序：由於排序記錄個數太多，不能同時放置在記憶體中，整個排序過程需要在內外存之間多次交換數據才能纔能進行。外部排序最常用的演算法是多路歸併排序
影響排序的三個方面
- 時間效能
  - 比較
  - 移動
- 輔助空間
- 演算法複雜度

交換排序

氣泡排序
- 基本思想：兩兩交換，將最大（或最小）的交換至佇列前

選擇排序

簡單選擇排序
- 基本思想：在未排序的序列種找到最小（或最大）的元素放到前面

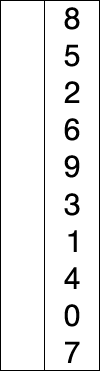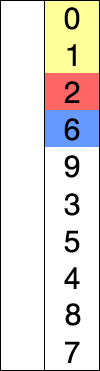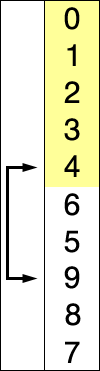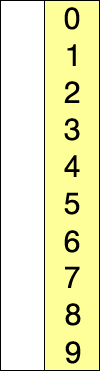
參考實現程式碼（cpp）

    template<typename T>
    void selectionSort(T arr[], int n){

        for(int i = 0 ; i < n ; i ++){

            int minIndex = i;
            for( int j = i + 1 ; j < n ; j ++ )
                if( arr[j] < arr[minIndex] )
                    minIndex = j;

            swap( arr[i] , arr[minIndex] );
        }
    }

直接選擇排序
樹型選擇排序

插入排序及其改進

直接插入排序

基本思想: 將未排序的元素插入到已經排好序的佇列種對應的位置

程式碼

template<typename T>
void insertionSort(T arr[], int n){
    for( int i = 1 ; i < n ; i ++ ) {

    // 尋找元素arr[i]合適的插入位置
    // 寫法1
    //        for( int j = i ; j > 0 ; j-- )
    //            if( arr[j] < arr[j-1] )
    //                swap( arr[j] , arr[j-1] );
    //            else
    //                break;

    // 寫法2
    //        for( int j = i ; j > 0 && arr[j] < arr[j-1] ; j -- )
    //            swap( arr[j] , arr[j-1] );

    // 寫法3
                T e = arr[i];
                int j; // j儲存元素e應該插入的位置
                for (j = i; j > 0 && arr[j-1] > e; j--)
                    arr[j] = arr[j-1];
                arr[j] = e;
    }
    return;
}

改進：

折半插入排序： 找到已排好序種對應位置時用折半查詢

希爾排序:

基本思想：交換不相鄰的元素以對陣列的區域性進行排序
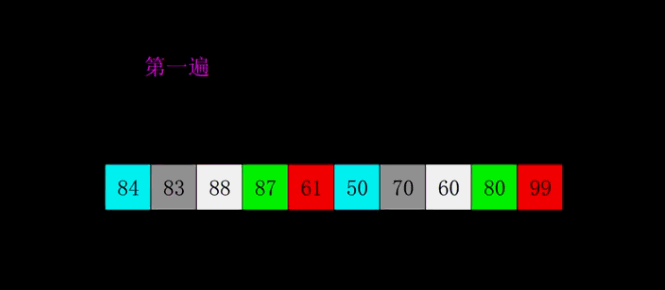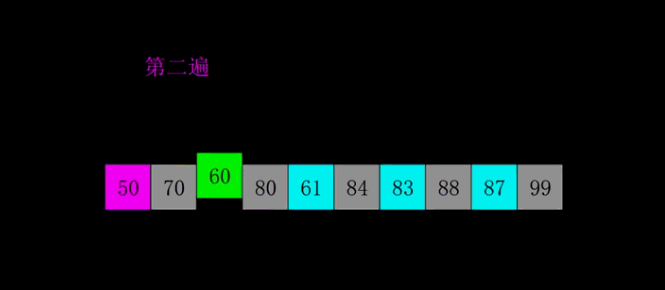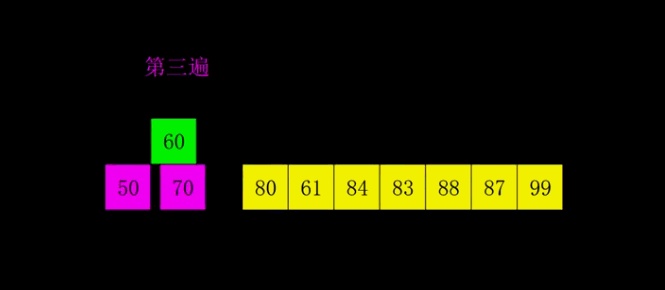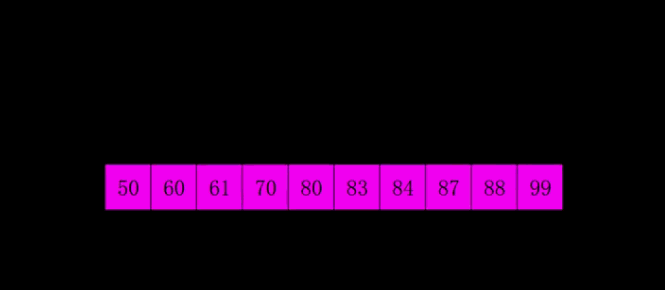
第一個O(n log n)的排序演算法

參考程式碼

template<typename T>
void shellSort(T arr[], int n){

    // 計算 increment sequence: 1, 4, 13, 40, 121, 364, 1093...
    int h = 1;
    while( h < n/3 )
        h = 3 * h + 1;

    while( h >= 1 ){

        // h-sort the array
        for( int i = h ; i < n ; i ++ ){

            // 對 arr[i], arr[i-h], arr[i-2*h], arr[i-3*h]... 使用插入排序
            T e = arr[i];
            int j;
            for( j = i ; j >= h && e < arr[j-h] ; j -= h )
                arr[j] = arr[j-h];
            arr[j] = e;
        }

        h /= 3;
    }
}

希爾排序及其優化

其他：路插入排序,表插入排序等。

第三章高階排序問題

歸併排序及其優化

基本思想： (分治)將排序序列差分成兩個等長的子序列，對子序列進行排序後再歸併

參考核心程式碼(cpp)

    // 使用優化的歸併排序演算法, 對arr[l...r]的範圍進行排序
    template<typename T>
    void __mergeSort2(T arr[], int l, int r){

        // 優化2: 對於小規模陣列, 使用插入排序
        if( r - l <= 15 ){
            insertionSort(arr, l, r);
            return;
        }

        int mid = (l+r)/2;
        __mergeSort2(arr, l, mid);
        __mergeSort2(arr, mid+1, r);

        // 優化1: 對於arr[mid] <= arr[mid+1]的情況,不進行merge
        // 對於近乎有序的陣列非常有效,但是對於一般情況,有一定的效能損失
        if( arr[mid] > arr[mid+1] )
            __merge(arr, l, mid, r);
    }

優化點：
- 當排序的元素少於一定（16）時，直接呼叫插入排序
- 如果第一個序列的最大值小於第二個序列的最小值，則不用比較，直接合併

歸併排序的自底向上寫法（迭代）

核心程式碼參考
```

  // 使用自底向上的歸併排序演算法
  template <typename T>
  void mergeSortBU(T arr[], int n){
      // Merge Sort Bottom Up 優化
      // 對於小陣列, 使用插入排序優化
      for( int i = 0 ; i < n ; i += 16 )
          insertionSort(arr,i,min(i+15,n-1));

      for( int sz = 16; sz < n ; sz += sz )
          for( int i = 0 ; i < n - sz ; i += sz+sz )
              // 對於arr[mid] <= arr[mid+1]的情況,不進行merge
              if( arr[i+sz-1] > arr[i+sz] )
                  __merge(arr, i, i+sz-1, min(i+sz+sz-1,n-1) );
      // Merge Sort BU 也是一個O(nlogn)複雜度的演算法，雖然只使用兩重for回圈
      // 所以，Merge Sort BU也可以在1秒之內輕鬆處理100萬數量級的數據
      // 注意：不要輕易根據回圈層數來判斷演算法的複雜度，Merge Sort BU就是一個反例
      // 關於這部分陷阱，推薦看（liubobo老師）的《玩轉演算法面試》課程，第二章：《面試中的複雜度分析》：）
  }
  ```

快速排序

基本思想：（分治）將選定的元素放到合適的位置，然後遞回排序被該元素分開的前後兩個子序列。(分出來的兩個子序列可能不等長，相差很大，會影響效能)

核心程式碼參考

```
// 對arr[l...r]部分進行partition操作
// 返回p, 使得arr[l...p-1] < arr[p] ; arr[p+1...r] > arr[p]
template <typename T>
int _partition(T arr[], int l, int r){

    // 隨機在arr[l...r]的範圍中, 選擇一個數值作爲標定點pivot
    swap( arr[l] , arr[rand()%(r-l+1)+l] );

    T v = arr[l];
    int j = l;
    for( int i = l + 1 ; i <= r ; i ++ )
        if( arr[i] < v ){
            j ++;
            swap( arr[j] , arr[i] );
        }

    swap( arr[l] , arr[j]);

    return j;
}

// 對arr[l...r]部分進行快速排序
template <typename T>
void _quickSort(T arr[], int l, int r){

    // 對於小規模陣列, 使用插入排序進行優化
    if( r - l <= 15 ){
        insertionSort(arr,l,r);
        return;
    }

    int p = _partition(arr, l, r);
    _quickSort(arr, l, p-1 );
    _quickSort(arr, p+1, r);
}
```

優化：
1. 標定點隨機選（針對基本有序的序列，如果固定選最前面的元素，則分治的兩個子問題不平衡，退化爲O(n^2)的複雜度）
2. 小規模排序，使用插入排序

雙路快排

基本思想：針對鍵值重複過多時，分治的兩個子序列不等長，導致分治不平衡

核心程式碼參考

// 雙路快速排序的partition
// 返回p, 使得arr[l...p-1] <= arr[p] ; arr[p+1...r] >= arr[p]
// 雙路快排處理的元素正好等於arr[p]的時候要注意，詳見下面 下麪的註釋：）
template <typename T>
int _partition2(T arr[], int l, int r){

    // 隨機在arr[l...r]的範圍中, 選擇一個數值作爲標定點pivot
    swap( arr[l] , arr[rand()%(r-l+1)+l] );
    T v = arr[l];

    // arr[l+1...i) <= v; arr(j...r] >= v
    int i = l+1, j = r;
    while( true ){
        // 注意這裏的邊界, arr[i] < v, 不能是arr[i] <= v
        // 思考一下爲什麼?
        while( i <= r && arr[i] < v )
            i ++;

        // 注意這裏的邊界, arr[j] > v, 不能是arr[j] >= v
        // 思考一下爲什麼?
        while( j >= l+1 && arr[j] > v )
            j --;

        // 對於上面的兩個邊界的設定, 有的同學在課程的問答區有很好的回答:)
        // 大家可以參考: http://coding.imooc.com/learn/questiondetail/4920.html

        if( i > j )
            break;

        swap( arr[i] , arr[j] );
        i ++;
        j --;
    }

    swap( arr[l] , arr[j]);

    return j;
}

// 對arr[l...r]部分進行快速排序
template <typename T>
void _quickSort(T arr[], int l, int r){

    // 對於小規模陣列, 使用插入排序進行優化
    if( r - l <= 15 ){
        insertionSort(arr,l,r);
        return;
    }

    // 呼叫雙路快速排序的partition
    int p = _partition2(arr, l, r);
    _quickSort(arr, l, p-1 );
    _quickSort(arr, p+1, r);
}

三路快排

基本思想：針對2路快排的加強，進一步解決鍵值重複過多的問題（增加一個等值區域）

核心程式碼參考

// 遞回的三路快速排序演算法
template <typename T>
void __quickSort3Ways(T arr[], int l, int r){

    // 對於小規模陣列, 使用插入排序進行優化
    if( r - l <= 15 ){
        insertionSort(arr,l,r);
        return;
    }

    // 隨機在arr[l...r]的範圍中, 選擇一個數值作爲標定點pivot
    swap( arr[l], arr[rand()%(r-l+1)+l ] );

    T v = arr[l];

    int lt = l;     // arr[l+1...lt] < v
    int gt = r + 1; // arr[gt...r] > v
    int i = l+1;    // arr[lt+1...i) == v
    while( i < gt ){
        if( arr[i] < v ){
            swap( arr[i], arr[lt+1]);
            i ++;
            lt ++;
        }
        else if( arr[i] > v ){
            swap( arr[i], arr[gt-1]);
            gt --;
        }
        else{ // arr[i] == v
            i ++;
        }
    }

    swap( arr[l] , arr[lt] );

    __quickSort3Ways(arr, l, lt-1);
    __quickSort3Ways(arr, gt, r);
}

template <typename T>
void quickSort3Ways(T arr[], int n){

    srand(time(NULL));
    __quickSort3Ways( arr, 0, n-1);
}
// 比較Merge Sort和雙路快速排序和三路快排三種排序演算法的效能效率
// 對於包含有大量重複數據的陣列, 三路快排有巨大的優勢
// 對於一般性的亂數組和近乎有序的陣列, 三路快排的效率雖然不是最優的, 但是是在非常可以接受的範圍裡
// 因此, 在一些語言中, 三路快排是預設的語言庫函數中使用的排序演算法。比如Java:)

歸併排序和快速排序衍生的問題

* 求逆序對（歸併排序）
* 求陣列中的第N大元素

第四章堆和堆排序

基本概念認識

佇列
- 普通佇列：先進先出
- 優先佇列：根據優先順序出隊
優先佇列應用 對動態的數據排序
優先佇列的三種實現方式

實現方式入隊出隊

普通陣列 O(1) O(n)

順序陣列(元素有序) O(n) O(1)

堆 O(log n) O(log n)

實現方式	入隊	出隊
普通陣列	O(1)	O(n)
順序陣列(元素有序)	O(n)	O(1)
堆	O(log n)	O(log n)

堆的基本儲存

* 用陣列儲存二元堆積
* 陣列的索引次序 對應 二元堆積中 層序遍歷次序
* 對於完全二元樹,對第i個元素，其與其父，其子的關係
    * 根節點索引從0開始
        * parent(i) = （i-1）/2
        * left child (i) = 2*i +1
        * right child (i) = 2*i + 2
    * 根節點索引從1開始
        * parent(i) = i/2
        * left child (i) = 2*i 
        * right child (i) = 2*i + 1

heapfy過程（堆的建立）

- 基本思想：從最後一個非葉子節點（索引爲count/2，在根節點索引從1開始的情況下）開始，shiftdown()，自底向上實現堆
- 將n個元素逐個插入空堆中，演算法複雜度爲O(n log n),而heapfy過程演算法複雜度O(n)  
- 程式碼
```
    // 建構函式, 通過一個給定陣列建立一個最大堆
    // 該構造堆的過程, 時間複雜度爲O(n)
    MaxHeap(Item arr[], int n){
        data = new Item[n+1];
        capacity = n;

        for( int i = 0 ; i < n ; i ++ )
            data[i+1] = arr[i];
        count = n;

        for( int i = count/2 ; i >= 1 ; i -- )
            shiftDown(i);
    }
```

ShiftUp(節點上移比較)

- 程式碼
    ```
        void shiftUp(int k){
        while( k > 1 && data[k/2] < data[k] ){
            swap( data[k/2], data[k] );
            k /= 2;
        }
        }
    ```

ShiftDown（節點下移比較）

- 程式碼
```
    void shiftDown(int k){
    while( 2*k <= count ){
        int j = 2*k; // 在此輪回圈中,data[k]和data[j]交換位置
        if( j+1 <= count && data[j+1] > data[j] )
            j ++;
        // data[j] 是 data[2*k]和data[2*k+1]中的最大值

        if( data[k] >= data[j] ) break;
        swap( data[k] , data[j] );
        k = j;
    }
    }
```

堆排序及其優化

* 堆排序演算法：
    * 建立堆： 一種通過不斷insert()建立O(nlogn)，一種傳入陣列用heapfy建立O(n)
    * 堆頂出堆： 將堆頂與堆尾互換，堆的size-1,並將新的堆頂（原堆尾）shiftDown()
    * 重複第二步  
* 堆排序的實現
    1. 藉助insert()建立堆
    ```
    // heapSort1, 將所有的元素依次新增到堆中, 在將所有元素從堆中依次取出來, 即完成了排序
    // 無論是建立堆的過程, 還是從堆中依次取出元素的過程, 時間複雜度均爲O(nlogn)
    // 整個堆排序的整體時間複雜度爲O(nlogn)
    template<typename T>
    void heapSort1(T arr[], int n){

        MaxHeap<T> maxheap = MaxHeap<T>(n);
        for( int i = 0 ; i < n ; i ++ )
            maxheap.insert(arr[i]);

        for( int i = n-1 ; i >= 0 ; i-- )
            arr[i] = maxheap.extractMax();

    }

    2. 藉助heapfy() 建立堆
    // heapSort2, 藉助我們的heapify過程建立堆
    // 此時, 建立堆的過程時間複雜度爲O(n), 將所有元素依次從堆中取出來, 實踐複雜度爲O(nlogn)
    // 堆排序的總體時間複雜度依然是O(nlogn), 但是比上述heapSort1效能更優, 因爲建立堆的效能更優
    template<typename T>
    void heapSort2(T arr[], int n){

        MaxHeap<T> maxheap = MaxHeap<T>(arr,n);
        for( int i = n-1 ; i >= 0 ; i-- )
            arr[i] = maxheap.extractMax();

    }
    ```
* 堆的實現細節
    *ShiftUp和ShiftDown種使用複製操作替換swap操作*

索引堆

基本思想：分索引陣列和數據陣列，數據陣列存數據元素。索引陣列按堆的次序（比較的是實際元素的鍵值）存對應節點的索引（地址）。ShiftUP和ShiftDown中比較(實際元素的值)，交換對應的索引（儲存地址），而不交換實際的元素。
一點理解：維護了一個數組，既能有堆的特性（取最值），又能保持原有陣列的儲存次序（數據陣列的索引是原陣列的+1）。

ShfitUp()

    // 索引堆中, 數據之間的比較根據data的大小進行比較, 但實際操作的是索引
    void shiftUp( int k ){
    while( k > 1 && data[indexes[k/2]] < data[indexes[k]] ){
        swap( indexes[k/2] , indexes[k] );
        k /= 2;
    }
}

ShiftDown()

    // 索引堆中, 數據之間的比較根據data的大小進行比較, 但實際操作的是索引
    void shiftDown( int k ){
        while( 2*k <= count ){
            int j = 2*k;
            if( j + 1 <= count && data[indexes[j+1]] > data[indexes[j]] )
                j += 1;
            if( data[indexes[k]] >= data[indexes[j]] )
                break;
            swap( indexes[k] , indexes[j] );
            k = j;
        }
    }

增刪實現 (插入操作不是很理解)

    // 向最大索引堆中插入一個新的元素, 新元素的索引爲i, 元素爲item
// 傳入的i對使用者而言,是從0索引的
void insert(int i, Item item){
    assert( count + 1 <= capacity );
    assert( i + 1 >= 1 && i + 1 <= capacity );
    i += 1;
    data[i] = item;
    indexes[count+1] = i;
    count++;
    shiftUp(count);
}

// 從最大索引堆中取出堆頂元素, 即索引堆中所儲存的最大數據
Item extractMax(){
    assert( count > 0 );

    Item ret = data[indexes[1]];
    swap( indexes[1] , indexes[count] );
    count--;
    shiftDown(1);
    return ret;
}

應用：最小生成樹Prim演算法中，用來維護每個節點對應的最小橫切面的權重【同時能輸出當前所有節點最小橫切面中的最小橫切面】

涉及堆的相關問題

- 多路歸併排序 多個元素同時比較的時候用，最小（大）堆
- d叉堆 d-ary heap  
- 最大最小佇列 （最大堆和最小堆同時維護？？）
- 二項堆
- 斐波那契堆

桶排序

基本思想： 分配 + 收集 （先排序低位再排序高位）

排序總結

排序	平均時間複雜度	原地排序	額外空間	穩定排序
插入排序（Insertion Sort）	O(n^2)	是	O(1)	是
歸併排序(Merge Sort)	O（nlogn）	否	O(n)	是
快速排序（Quick Sort）	O(nlogn)	是	O（logn）	否
堆排序（Heap Sort)	O(nlogn)	是	O(1)	否

不同排序演算法的選擇
- n較小：直接插入排序或直接選擇排序
- 基本有序序列，直接插入，冒泡，隨機的快速排序
- n較大，應選複雜度好的：快速排序，歸併排序，堆排序。
  - 快速排序效能平均最好，堆排序更少的輔助空間，歸併排序是穩定的排序。（當排序數少於一定時如16，呼叫直接插入排序）

其他參考
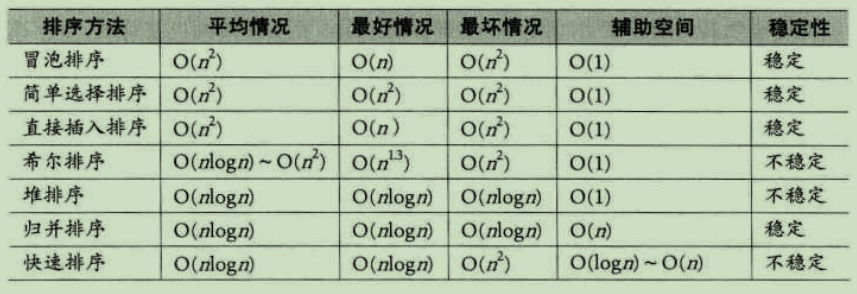
排序算法总结
排序对比

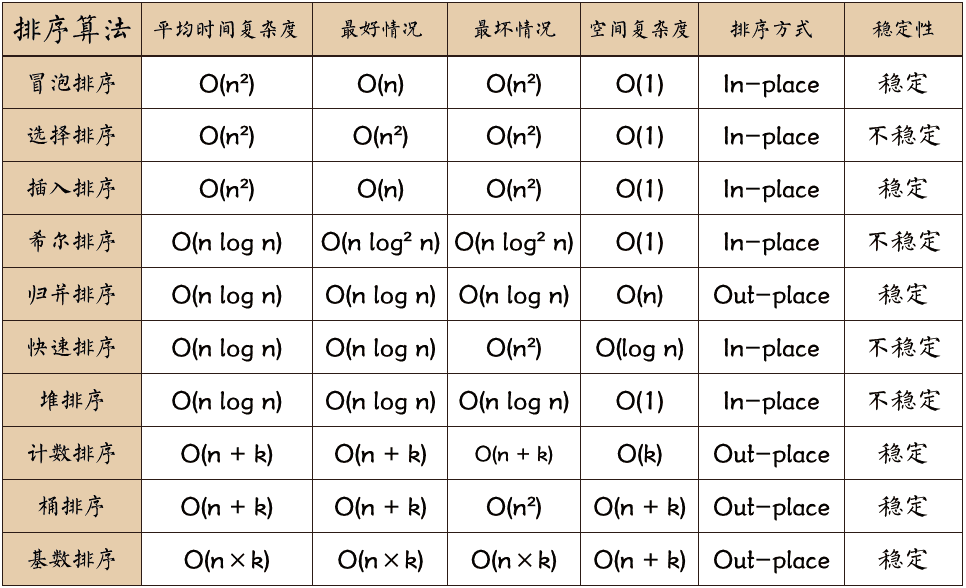
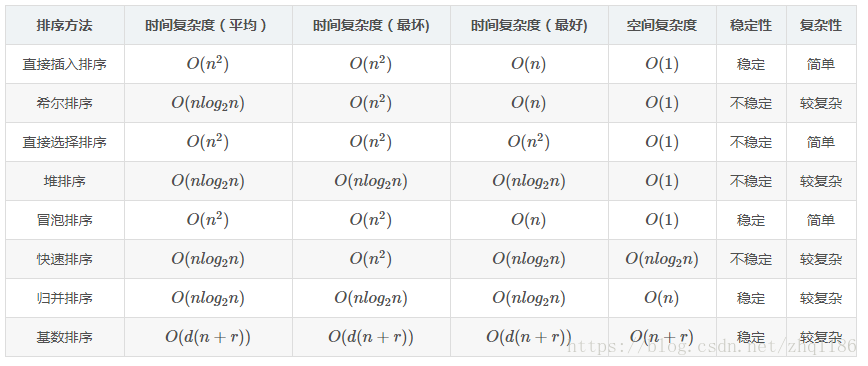
C語言中的14種排序
 14中排序動畫演示

第五章二分搜尋樹

5-1 二分查詢法

基本思想：（遞回分治）對有序序列，不需要逐一比較，只要比較中間值，然後確定目標值的可能區域，再在可能區域遞回二分查詢。
細節：
1. 計算中間值時，注意防止越界（基本型別的範圍）。
  - 合理寫法： int mid = left + (right-left)/2 ，
  - 危險寫法： int mid = (left + right)/2
2. 二分查詢返回的只有一個索引，而序列中可能存在重複值。如何返回所有重複值？
  - 練習：對於存在重複值的序列，返回目標值索引的floor(第一個索引)和ceil（最後一個索引）
改進：（選不同的分割點）
- 插值查詢（按比值分割）
  - mid = left + (right-left)*{(key-a[left])/(a[right]-a[left])}
- 斐波那契查詢
  - mid = left + F_block - 1 (黃金分割)

5-2 二分搜尋樹

二分搜尋樹的定義：
- 左子樹>(<) 根 >(<) 右子樹 [一般不考慮鍵值重複的問題]
二分搜尋樹的優勢
- 高效(（O(nlogn))的維護數據的有序性：min,max,floor,ceil,rank,select

二分搜尋樹的節點插入

實現方式：

遞回(返回子樹根節點)[從根節點開始搜尋，找到key值則替換，未找到則根據比較關係遞回子樹]

    // 向以node爲根的二分搜尋樹中, 插入節點(key, value), 使用遞回演算法
    // 返回插入新節點後的二分搜尋樹的根
    private Node insert(Node node, Key key, Value value)\{

        if( node == null ){
            count ++;
            return new Node(key, value);
        }

        if( key.compareTo(node.key) == 0 )
            node.value = value;
        else if( key.compareTo(node.key) < 0 )
            node.left = insert( node.left , key, value);
        else    // key > node->key
            node.right = insert( node.right, key, value);

        return node;
    }

迭代
- 當作練習

二分搜尋書的查詢
- 基本思想: 二分查詢
二分搜尋樹的遍歷
- （深度優先遍歷）
  - 前序遍歷，中序遍歷，後序遍歷
- （廣度優先遍歷）
  - 層序遍歷
刪除最大值，最小值
- 實現：
  - 遞回：（不斷遞回(左/右)子樹，直到節點沒有（左/右）子樹，刪除該節點，返回其的（右/左）子樹賦值給上一節點的（左/右）子樹）
刪除Key對應的節點
- 實現：
  - 遞回
    - 從根節點開始遞回搜尋
      - 如果目標值在根節點則刪除根節點，選新的中間值上位（左子樹最右（大/小）的節點，右子樹最左（小/大）的節點）
      - 否則根據比較次序，選擇（左/右）子樹遞回搜尋，根節點的（左/右）子樹 = 返回刪除最值後的子樹的根節點

5-3 二分搜尋樹的特性

順序性
- minimum/maximum
- successor/predecessor 後繼/前繼
- floor/ceil （存在鍵值重複時，索引的範圍）
- rank/select 已知key獲取排名/已知排名獲取key,value
侷限性：(不平衡) 依照順序或逆序插入元素，二分搜尋樹退化爲鏈表（跟節點爲第一個元素，在最左，或最右）。
支援重複鍵值的二分搜尋樹
- 思路一：讓鍵值重複節點的右子樹或左子樹包含鍵值重複的節點。
- 思路二：每個節點增加一個區域（鏈表或陣列），存鍵值相等的元素

二叉平衡樹

- 平衡二元樹：
    - 左右子樹高度差不超過1的二元搜尋樹，即平衡二元樹所有結點的平衡因子絕對值不超過1（平衡因子 = 結點左子樹的高度 - 結點右子樹的高度）。
- 實現方式：
    - AVL樹
    - 紅黑樹
    - 2-3樹
    - Splay樹

AVL 樹

基本思想，每插入一個節點，自底向上維護樹的平衡，以及每個節點的平衡因子
平衡調整的四種類型：
- LL型右旋調整調整後涉及到的節點的平衡因子（bf）均爲0
- RR型左旋調整調整後涉及到的節點的平衡因子(bf)均爲0
- LR型先左旋調整至LL型，然後右旋調整 bf的維護如下：
- RL型先右旋調整至RR型，然後左旋調整
  [外連圖片轉存失敗,源站可能有防盜鏈機制機製,建議將圖片儲存下來直接上傳(img-5QTnPk8V-1597323215794)(/source/pictures/平衡調整的四種類型.bmp)]
插入操作思路整理：
- 考慮當前節點的子樹是否新增了新節點
  - 沒有則不用維護，直接返回
  - 左子樹新增了新節點 >>> 當前節點的平衡因子要加一( $bf= bf+1$ )
    - 若 $bf>1$ (需要平衡調整) >>> 進行左平衡調整
  - 右子樹新增了新節點 >>> 當前節點的平衡因子要減一( $bf = bf -1$ )
    - 若 $bf<-1$ ，需要平衡調整 >>> 進行右平衡調整
左平衡調整(cur.bf > 1)
- 看cur的左子節點L 的平衡因子 L.bf
  - L.bf == 1 >>> LL型 >>> 右旋操作
  - L.bf == -1 >>> LR型 >>> 先左旋調整至LL型，然後右旋調整
右平衡調整(cur.bf < -1)
- 看cur節點的右孩子節點R 的平衡因子R.bf
  - R.bf == -1 >>> RR型 >>> 左旋操作
  - R.bf == 1 >>> RL型 >>> 先右旋調整至RR型，然後左旋調整
插入操作程式碼

	//插入操作
	void insert(K key,V value) {
		taller = false; //增加了新的一層？？
		root = __insert(root,key,value);
	}
	
	//返回插入新節點後的根節點
	private AVLNode __insert(AVLNode curNode,K key,V value) {
		if(curNode==null) {
			curNode = new AVLNode(key,value);
			taller = true; //增加了新節點
			return curNode;//
		}
		else {
			if(key.compareTo(curNode.key)==0) {
				return curNode;//節點已經存在，返回（不覆蓋舊值）
			}
			else if(key.compareTo(curNode.key)<0) {
				curNode.left = __insert(curNode.left,key,value); //往左子樹新增節點
				if(taller) {//增加了新節點
					switch(curNode.bf) {
						case 0: //新增節點沒有打破平衡，但bf+1
							curNode.bf = 1;//左邊新加一個點
							taller = true;//此處很重要，自底 向上傳遞平衡資訊
							break;
						case 1:  //本來左子樹多一個結點，然後taller爲true,左子樹又增加了一個結點
							curNode = leftBalance(curNode); //左平衡時必須保證 curNode具有左孩子
							taller = false; //左平衡後 達到平衡
							break;
						case -1: //新增節點使得curNode左右平衡
							curNode.bf = 0;
							taller = false;
							break;
					}
				}
				return curNode;
			}
			else { //往當前節點的右子樹增添節點
				curNode.right = __insert(curNode.right,key,value);//往右子樹增加節點
				if(taller) {
					switch(curNode.bf) {
						case 0:
							curNode.bf = -1;
							taller = true;
							break;
						case 1:
							 curNode.bf = 0;
							 taller = false;
							 break;
						case -1:
							curNode = rightBalance(curNode);
							taller = false;
							break;		
					}
				}
				return curNode;
			}
		}
	}

左平衡調整程式碼

	/*
	 * 左平衡操作
	 */
	//[當前curNode的bf>0，又再左子樹增加節點時需要左平衡操作]
	AVLNode leftBalance(AVLNode curNode) {
		AVLNode L = curNode.left;
		if(L.bf==1) { //LL型需要左旋
			curNode.bf = 0;//右旋平衡
			L.bf = 0;//右旋平衡
			return rightRotate(curNode);
		}
		else if(L.bf==-1) {//LR型需要 先左旋  後右旋
			AVLNode LR = L.right; //左孩子的右孩子
			//以下程式碼不是很理解,,,畫一下實際例子可以明白，，但爲啥子LR.bf不會一直被維護爲0？（因爲LR不一定是新增節點?）
			switch(LR.bf) {
				case 1:
					curNode.bf = -1;
					L.bf = 0;
					break;
				case 0:
					curNode.bf = 0;
					L.bf = 0;
					break;
				case -1:
					curNode.bf = 0;
					L.bf = 1;
					break;
			}
			LR.bf = 0;
			curNode.left = leftRotate(curNode.left);
			return rightRotate(curNode);
		}
		else {//不需要左平衡處理
			return curNode;
		}
	}

右平衡調整程式碼

	//右平衡操作
	/*
	 * curNode bf本已經-1的基礎上，在右方又新增節點
	 */
	AVLNode rightBalance(AVLNode curNode) {
		AVLNode R = curNode.right;
		if(R.bf==-1) { //RR型 
			curNode.bf = 0;
			R.bf = 0;
			return leftRotate(curNode);
		}
		else if(R.bf==1) {//RL型
			AVLNode RL = R.left;
			switch(RL.bf) {
				case 0:
					curNode.bf = 0;
					R.bf = 0;
					break;
				case 1:
					R.bf =-1;
					curNode.bf = 0;
					break;
				case -1:
					curNode.bf = 1;
					R.bf = 0;
					break;
			}
			RL.bf = 0;
			curNode.right = rightRotate(R);
			return leftRotate(curNode);
			
		}
		else {
			return curNode;
		}
	}

左旋操作

	//左旋操作
	AVLNode leftRotate(AVLNode curNode) {
		AVLNode subRoot = curNode.right;
		curNode.right = subRoot.left;
		subRoot.left = curNode;
		return subRoot;
	}

右旋操作

	//右旋操作
	AVLNode rightRotate(AVLNode curNode) {
		AVLNode subRoot = curNode.left;//左孩子上位
		curNode.left = subRoot.right;//把你的右孩子給我，作爲我的左孩子(保證排序性)
		subRoot.right = curNode;//你上位後我成爲你的有孩子
		return subRoot;
	}

其他操作實現：
- 可參考<<數據結構從應用到時間（Java版）>>

5-5 多路查詢樹

多路查詢樹的意義

對於樹來說，一個結點只能儲存一個元素，那麼在元素非常多的時候，就會使得要麼樹的度非常大（結點擁有子樹的個數的最大值），要麼樹的高度非常大，甚至兩者都必須足夠大才行，這就使得記憶體存取外存次數非常多，這顯然成了時間效率上的瓶頸，這迫使我們要打破每一個結點只儲存一個元素的限制，爲此引入了多路查詢樹的概念
2-3 樹
- 每個結點都具有兩個孩子（我們稱它爲 2 結點）或三個孩子（我們稱它爲 3 結點）的樹
- 特性
  一個 2 結點包含一個元素和兩個孩子（或沒有孩子），且左子樹數據元素小於該元素右子樹數據元素大於該元素
  一個 3 結點包含一小一大兩個元素和三個孩子（或沒有孩子）
  如果有 3 個孩子的話
  左子樹包含小於較小元素的元素
  右子樹包含大於較大元素的元素
  中間子樹包含介於兩元素之間的元素
2-3-4 樹
B 樹

5-6 樹形問題和更多樹。

平衡二元樹和堆的結合Treap
trie ：查詢效率與單詞長度有關，與單詞中的單詞數量無關
其他樹形(遞回)問題：
- 一條龍遊戲
- 8 數碼問題
- 8 皇後問題
- 數獨
- 搬運工
更多樹的結構
- KD樹
- 區間樹
- 哈夫曼樹

第六章:並查集

6-1 並查集基礎

解決的問題：
- 連線問題，數學中集合類的實現，
- 路徑問題
並查集的基本方法
- union(p,q) 將p與q 聯合（同屬一個集合（連通分支））
- find§ 查詢p所在集合序號
- isConnect(p,q)
並查集的實現
- 陣列實現（QuickFind）（陣列索引爲元素鍵值，陣列值爲對應的集合號）
  - union(p,q) 需要遍歷更新所有元素的集合號，時間複雜度O(n)
  - find§ 直接陣列下標查詢，O(1)
  - isConnect() 複雜度O(1)
- 樹形實現（陣列索引爲元素鍵值，陣列值爲該節點的父節點的索引）
  - union(p,q) 時間複雜度O(h)，h爲樹的高度
  - find§ 需要回溯到(所在分支的)跟節點，O(h)，h爲樹的高度
  - isConnect() 複雜度O(h，h爲樹的高度
  - 樹形實現中 union() 的三種實現方式（不斷改進（降低）樹的高度h）
    - 隨機合併
    - 基於size的優化
      - 維護一個size陣列，存每個分支的元素多少
      - 將元素較少的樹合併到元素較多的的樹新的分支size = size1 + size2
    - 基於rank的優化
      - 維護一個rank陣列，存每個分支對應樹的高度
      - 將高度小的和平到高度大的
  - find() 過程中的路徑壓縮（降低樹的高度）
    - 基本思想：基於樹形實現的並查集，在find()時，需要回溯到分支樹的根節點，在回溯的過程，可以將樹的高度進行調整。
    - 具體實現思路：回溯過程中，將當前節點的父節點不斷向上更新
    - 程式碼
```
    // 查詢過程, 查詢元素p所對應的集合編號
    // O(h)複雜度, h爲樹的高度
    private int find(int p){
        assert( p >= 0 && p < count );

        // path compression 1
        while( p != parent[p] ){
            parent[p] = parent[parent[p]]; //指向父節點的父節點
            p = parent[p];
        }
        return p;

        // path compression 2, 遞回演算法
//            if( p != parent[p] )
//                parent[p] = find( parent[p] );
//            return parent[p];
    }
```
並查集的應用
- 題目
  - leetcode130_被圍繞的區域

第七章: 圖

7-1 圖論基礎

圖的應用
- 通訊網路
- 社羣網路
- 狀態機等
圖的分類
- 無權圖與有權圖
- 有向圖與無向圖
圖的表示
- （n,m） n個頂點，m條邊
- 鄰接矩陣 $n * n$ 矩陣適合稠密圖
- 鄰接表適合稀疏圖
- 其他

7-2 相鄰點迭代器

圖遍歷過程中，避不開的便是遍歷當前節點的相鄰節點
迭代器的思想：對外提供存取數據的功能，同時避免內部數據直接暴露在外
複雜度分析
- 鄰接矩陣 O(n)
- 鄰接表 O(m)

7-4 圖的演算法框架

讀圖方式（僅限本課程）
- 不斷新增邊（需要知道頂點數）

7-5 深度優先遍歷和聯通分量

深度優先遍歷（DFS)
- 基本思想遞回
- 複雜分析
  - 鄰接表O（V+E）
  - 鄰接矩陣O(V^2)
求連通分支
- 維護一個size爲頂點數的vis陣列（可以存每個節點是否被存取，也可以每個節點存屬於哪個分支）
- 對每一個沒有被存取的節點進行深度優先遍歷
尋路
- 維護一個from 陣列，from[i]存第i個節點在dfs(s)過程中的上一個節點
- 從 $s$ 節點開始 dfs()
- 從目的點d 開始，根據from陣列回溯，得到s到d的路徑

7-7 廣度優先遍歷和最短路徑

廣度優先遍歷
- 基本思想迭代
- 實現細節
  - 處理環：相對於樹來說圖存在環的可能，所以遍歷的時候是將加入佇列的元素標記爲已存取，而不是存取結點時才標記。
- 複雜度分析
  - 鄰接表O（V+E）
  - 鄰接矩陣O(V^2)
- 求無權圖的 最短路徑
  - 維護一個from（回溯）陣列，from[i]存第i個節點到dfs(s)過程中的上一個節點
  - 維護一個order陣列， order[i] 存第i個節點在從s開始的bfs過程中的第幾層（最短距離）
  - 從 $s$ 節點開始 bfs()
  - 從 d 開始，根據from陣列回溯

7-8 更多無權圖的應用

迷宮生成，ps摳圖等

第八章：最小生成樹

8-1 最小生成樹問題和切分定理

最小生成樹的應用
- 電纜佈線設計，網路設計，電路設計等。
最小生成樹的適用範圍
- 主要針對帶權無向連通圖
切分定理
- 相關概念
  - 切分
  - 橫切邊
- 切分定理：給定任意切分，橫切邊中權值最小的邊必然屬於最小生成樹

8-2 Prim演算法及其優化

Lazy Prim 演算法
- 基本思想：迭代/遞回貪心（每次根據切分定理得到區域性最優）動態規劃？
- 演算法流程
  - 遞回/迭代遍歷節點
  - 將節點集合分爲已經被存取過的節點和未被存取過的節點，並將切分這兩個集合的橫切邊存入最小堆中
  - 每次選擇最小堆中的橫切邊出堆
    - 若該橫切邊的兩個端點均已經被存取，丟棄該邊，不做操作
    - 否則，將該邊加入最小生成樹中，繼續遍歷該邊中未被存取的點。
- lazy體現在（侷限性）:
  - 最小堆中，維護的橫切邊中，有很多不再時橫切邊的沒有及時丟棄。
  - 複雜度 O(ElogE)
Prim演算法的優化
- 用索引堆 (pq)來維護
  - 每個已經被存取的點對應的最小橫切邊的權重。pq.get（i）表示第i個節點關聯的當前最小橫切邊權重
  - 上述橫切邊集閤中的最小橫切邊的權重（最小中的最小）（及堆頂）
  - 用 edgeTo 輔助維護邊的資訊（起始點）
- 用 vis 陣列來維護節點是否已被存取
- Prim 演算法流程
  - 初始化：將起始點的橫切邊的權值加入索引堆pq中，起始點標記爲已經被存取
  - 回圈：
    - 選pq中最小權值的橫切邊e 加入到最小生成樹的邊集合
    - 遞回選出來邊e的兩個端點中未被存取的節點v：
      - 端點v 標記爲已經被存取
      - 遍歷端點v 的鄰接邊adjEdge，鄰接邊的另一個端點w
        
        保證**pq[w]**小（(與w節點關聯的當前最小橫切邊的權重）
        
        若pq[w]) 爲空，則將 adjEdge 的權重更新至 pq[w]
        
        或者若adjEdge的權重小於 pq[w] 則將 adjEdge 的權重更新至pq[w]
- 複雜度分析 O(ElogV)

8-3 Krusk演算法

基本思想：貪心不斷將不與已新增的邊構成圈的最小邊 加入到生成樹邊集合種
數據結構
- 用最小堆，維護邊集合，保證每次能取出剩餘邊中的最小邊
- 用並查集，維護節點在當前生成樹邊集合下的連通度，判斷新增邊是否構成環
演算法流程
- 對邊進行排序(複雜度O(ElogE))，用最最小堆來維護邊集合。
- 將最小邊出堆，並加入生成樹的集合。
- 回圈開始：
  - 將剩餘邊集閤中最小邊出堆
    - 判斷改邊與生成樹邊集閤中的邊是否構成環（用並查集判斷）
      - 若成環拋棄，繼續找下一個邊
      - 將改邊加入生成樹的邊集合
複雜度分析 O(ElogE)

8-6 最小生成樹演算法的思考

其他最小生成樹的演算法
- Vyssotsky’s Algorithm 將邊逐漸新增到生成樹中，一旦形成環，刪除環中權值最大的邊

慕課網-演算法與數據結構—學習總結

title: 慕課網-演算法與數據結構—學習總結 date: 2020-08-12 16:21:41 tags: LearnNotes

第一章 引言

第二章 排序基礎

交換排序

選擇排序

插入排序及其改進

第三章 高階排序問題

歸併排序及其優化

快速排序

歸併排序和快速排序衍生的問題

第四章 堆和堆排序

基本概念認識

堆的基本儲存

heapfy過程（堆的建立）

ShiftUp(節點上移比較)

ShiftDown（節點下移比較）

堆排序及其優化

索引堆

涉及堆 的相關問題

桶排序

排序總結

第五章 二分搜尋樹

5-1 二分查詢法

5-2 二分搜尋樹

5-3 二分搜尋樹的特性

二叉平衡樹

AVL 樹

5-5 多路查詢樹

5-6 樹形問題和更多樹。

第六章:並查集

6-1 並查集基礎

第七章: 圖

7-1 圖論基礎

7-2 相鄰點迭代器

7-4 圖的演算法框架

7-5 深度優先遍歷和聯通分量

7-7 廣度優先遍歷和最短路徑

7-8 更多無權圖的應用

第八章：最小生成樹

8-1 最小生成樹問題和切分定理

8-2 Prim演算法及其優化

8-3 Krusk演算法

8-6 最小生成樹演算法的思考

第九章：最短路徑

9-1 最短路徑問題和鬆弛操作

9-2 Dijkstra演算法的思想

9-3 實現Dijkstra演算法

9-4 負權邊和Bellman-Ford演算法

9-5 實現Bellman-Ford演算法

9-6 更多和最短路徑相關的思考

第十章：結束語

title: 慕課網-演算法與數據結構—學習總結
date: 2020-08-12 16:21:41
tags: LearnNotes

第一章引言

第二章排序基礎

第三章高階排序問題

第四章堆和堆排序

涉及堆的相關問題

第五章二分搜尋樹