Numpy

學習目標

瞭解Numpy運算速度上的優勢
知道陣列的屬性，形狀、型別
應用Numpy實現陣列的基本操作
應用亂數組的建立實現正態分佈應用
應用Numpy實現陣列的邏輯運算
應用Numpy實現陣列的統計運算
應用Numpy實現陣列之間的運算

4.1 Numpy優勢

學習目標

目標
- 瞭解Numpy運算速度上的優勢
- 知道Numpy的陣列記憶體塊風格
- 知道Numpy的並行化運算

1 Numpy介紹

Numpy（Numerical Python）是一個開源的Python科學計算庫，用於快速處理任意維度的陣列。

Numpy支援常見的陣列和矩陣操作。對於同樣的數值計算任務，使用Numpy比直接使用Python要簡潔的多。

Numpy使用ndarray物件來處理多維陣列，該物件是一個快速而靈活的大數據容器。

2 ndarray介紹

NumPy provides an N-dimensional array type, the ndarray, 
which describes a collection of 「items」 of the same type.

NumPy提供了一個N維陣列型別ndarray，它描述了相同類型的「items」的集合。

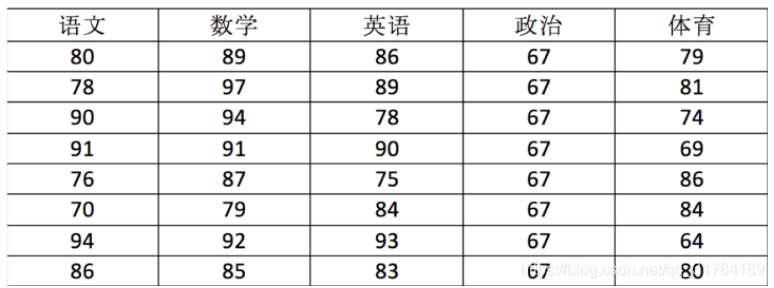
用ndarray進行儲存：

import numpy as np

# 建立ndarray
score = np.array(
[[80, 89, 86, 67, 79],
[78, 97, 89, 67, 81],
[90, 94, 78, 67, 74],
[91, 91, 90, 67, 69],
[76, 87, 75, 67, 86],
[70, 79, 84, 67, 84],
[94, 92, 93, 67, 64],
[86, 85, 83, 67, 80]])

score

返回結果：

array([[80, 89, 86, 67, 79],
       [78, 97, 89, 67, 81],
       [90, 94, 78, 67, 74],
       [91, 91, 90, 67, 69],
       [76, 87, 75, 67, 86],
       [70, 79, 84, 67, 84],
       [94, 92, 93, 67, 64],
       [86, 85, 83, 67, 80]])

提問:

使用Python列表可以儲存一維陣列，通過列表的巢狀可以實現多維陣列，那麼爲什麼還需要使用Numpy的ndarray呢？

3 ndarray與Python原生list運算效率對比

在這裏我們通過一段程式碼執行來體會到ndarray的好處

import random
import time
import numpy as np
a = []
for i in range(100000000):
    a.append(random.random())

# 通過%time魔法方法, 檢視當前行的程式碼執行一次所花費的時間
%time sum1=sum(a)

b=np.array(a)

%time sum2=np.sum(b)

其中第一個時間顯示的是使用原生Python計算時間,第二個內容是使用numpy計算時間:

CPU times: user 852 ms, sys: 262 ms, total: 1.11 s
Wall time: 1.13 s
CPU times: user 133 ms, sys: 653 µs, total: 133 ms
Wall time: 134 ms

從中我們看到ndarray的計算速度要快很多，節約了時間。

機器學習的最大特點就是大量的數據運算，那麼如果沒有一個快速的解決方案，那可能現在python也在機器學習領域達不到好的效果。

Numpy專門針對ndarray的操作和運算進行了設計，所以陣列的儲存效率和輸入輸出效能遠優於Python中的巢狀列表，陣列越大，Numpy的優勢就越明顯。

思考：

ndarray爲什麼可以這麼快？

4 ndarray的優勢

4.1 記憶體塊風格

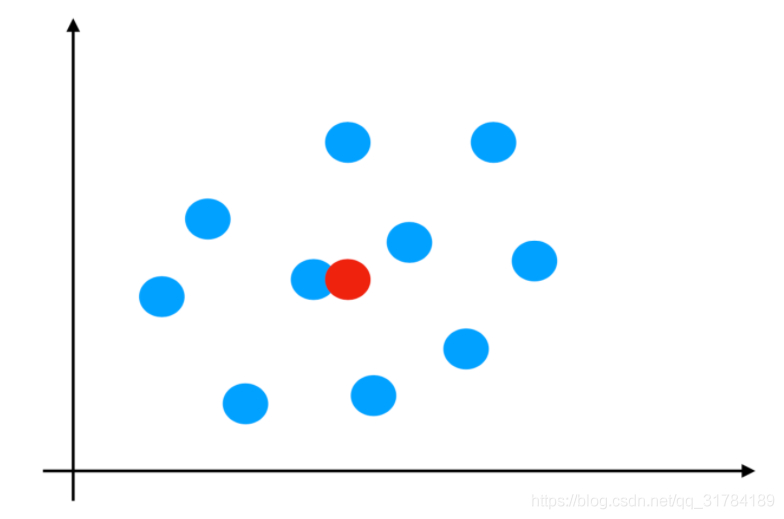
ndarray到底跟原生python列表有什麼不同呢，請看一張圖：

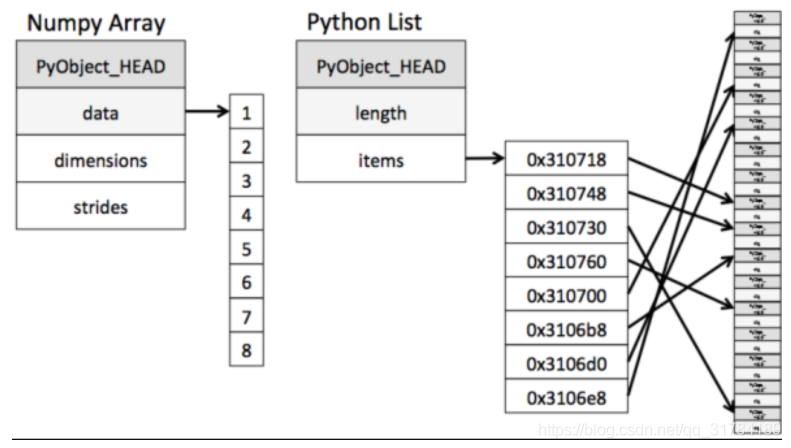
從圖中我們可以看出ndarray在儲存數據的時候，數據與數據的地址都是連續的，這樣就給使得批次運算元組元素時速度更快。

這是因爲ndarray中的所有元素的型別都是相同的，而Python列表中的元素型別是任意的，所以ndarray在儲存元素時記憶體可以連續，而python原生list就只能通過定址方式找到下一個元素，這雖然也導致了在通用效能方面Numpy的ndarray不及Python原生list，但在科學計算中，Numpy的ndarray就可以省掉很多回圈語句，程式碼使用方面比Python原生list簡單的多。

4.2 ndarray支援並行化運算（向量化運算）

numpy內建了並行運算功能，當系統有多個核心時，做某種計算時，numpy會自動做並行計算

4.3 效率遠高於純Python程式碼

Numpy底層使用C語言編寫，內部解除了GIL（全域性直譯器鎖），其對陣列的操作速度不受Python直譯器的限制，所以，其效率遠高於純Python程式碼。

5 小結

numpy介紹【瞭解】
- 一個開源的Python科學計算庫
- 計算起來要比python簡潔高效
- Numpy使用ndarray物件來處理多維陣列
ndarray介紹【瞭解】
- NumPy提供了一個N維陣列型別ndarray，它描述了相同類型的「items」的集合。
- 生成numpy物件:np.array()
ndarray的優勢【掌握】
- 記憶體塊風格
  - list -- 分離式儲存,儲存內容多樣化
  - ndarray -- 一體式儲存,儲存型別必須一樣
- ndarray支援並行化運算（向量化運算）
- ndarray底層是用C語言寫的,效率更高,釋放了GIL

===============================================

4.2 N維陣列-ndarray

學習目標

目標
- 說明陣列的屬性，形狀、型別

1 ndarray的屬性

陣列屬性反映了陣列本身固有的資訊。

屬性名字	屬性解釋
ndarray.shape	陣列維度的元組
ndarray.ndim	陣列維數
ndarray.size	陣列中的元素數量
ndarray.itemsize	一個數組元素的長度（位元組）
ndarray.dtype	陣列元素的型別

2 ndarray的形狀

首先建立一些陣列。

# 建立不同形狀的陣列
>>> a = np.array([[1,2,3],[4,5,6]])
>>> b = np.array([1,2,3,4])
>>> c = np.array([[[1,2,3],[4,5,6]],[[1,2,3],[4,5,6]]])

分別列印出形狀

>>> a.shape
>>> b.shape
>>> c.shape

(2, 3)  # 二維陣列
(4,)    # 一維陣列
(2, 2, 3) # 三維陣列

如何理解陣列的形狀？

二維陣列：

三維陣列：

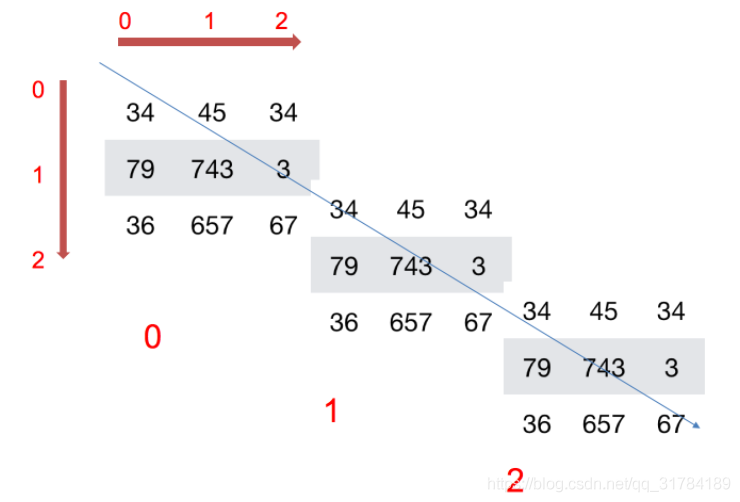
3 ndarray的型別

>>> type(score.dtype)

<type 'numpy.dtype'>

dtype是numpy.dtype型別，先看看對於陣列來說都有哪些型別

名稱	描述	簡寫
np.bool	用一個位元組儲存的布爾型別（True或False）	'b'
np.int8	一個位元組大小，-128 至 127	'i'
np.int16	整數，-32768 至 32767	'i2'
np.int32	整數，-2^31 至 2^32 -1	'i4'
np.int64	整數，-2^63 至 2^63 - 1	'i8'
np.uint8	無符號整數，0 至 255	'u'
np.uint16	無符號整數，0 至 65535	'u2'
np.uint32	無符號整數，0 至 2^32 - 1	'u4'
np.uint64	無符號整數，0 至 2^64 - 1	'u8'
np.float16	半精度浮點數：16位元，正負號1位，指數5位，精度10位	'f2'
np.float32	單精度浮點數：32位元，正負號1位，指數8位元，精度23位	'f4'
np.float64	雙精度浮點數：64位元，正負號1位，指數11位，精度52位	'f8'
np.complex64	複數，分別用兩個32位元浮點數表示實部和虛部	'c8'
np.complex128	複數，分別用兩個64位元浮點數表示實部和虛部	'c16'
np.object_	python物件	'O'
np.string_	字串	'S'
np.unicode_	unicode型別	'U'

建立陣列的時候指定型別

>>> a = np.array([[1, 2, 3],[4, 5, 6]], dtype=np.float32)
>>> a.dtype
dtype('float32')

>>> arr = np.array(['python', 'tensorflow', 'scikit-learn', 'numpy'], dtype = np.string_)
>>> arr
array([b'python', b'tensorflow', b'scikit-learn', b'numpy'], dtype='|S12')

注意：若不指定，整數預設int64，小數預設float64

4 總結

陣列的基本屬性【知道】

屬性名字	屬性解釋
ndarray.shape	陣列維度的元組
ndarray.ndim	陣列維數
ndarray.size	陣列中的元素數量
ndarray.itemsize	一個數組元素的長度（位元組）
ndarray.dtype	陣列元素的型別

=============================================

4.3 基本操作

學習目標

目標
- 理解陣列的各種生成方法
- 應用陣列的索引機制機製實現陣列的切片獲取
- 應用維度變換實現陣列的形狀改變
- 應用型別變換實現陣列型別改變
- 應用陣列的轉換

1 生成陣列的方法

1.1 生成0和1的陣列

np.ones(shape, dtype)
np.ones_like(a, dtype)
np.zeros(shape, dtype)
np.zeros_like(a, dtype)

ones = np.ones([4,8])
ones

返回結果:

array([[1., 1., 1., 1., 1., 1., 1., 1.],
       [1., 1., 1., 1., 1., 1., 1., 1.],
       [1., 1., 1., 1., 1., 1., 1., 1.],
       [1., 1., 1., 1., 1., 1., 1., 1.]])

np.zeros_like(ones)

返回結果:

array([[0., 0., 0., 0., 0., 0., 0., 0.],
       [0., 0., 0., 0., 0., 0., 0., 0.],
       [0., 0., 0., 0., 0., 0., 0., 0.],
       [0., 0., 0., 0., 0., 0., 0., 0.]])

1.2 從現有陣列生成

1.2.1 生成方式

np.array(object, dtype)
np.asarray(a, dtype)

a = np.array([[1,2,3],[4,5,6]])
# 從現有的陣列當中建立
a1 = np.array(a)
# 相當於索引的形式，並沒有真正的建立一個新的
a2 = np.asarray(a)

1.2.2 關於array和asarray的不同

1.3 生成固定範圍的陣列

1.3.1 np.linspace (start, stop, num, endpoint)

建立等差陣列 — 指定數量
參數:
- start:序列的起始值
- stop:序列的終止值
- num:要生成的等間隔樣例數量，預設爲50
- endpoint:序列中是否包含stop值，預設爲ture

# 生成等間隔的陣列
np.linspace(0, 100, 11)

返回結果：

array([  0.,  10.,  20.,  30.,  40.,  50.,  60.,  70.,  80.,  90., 100.])

1.3.2 np.arange(start,stop, step, dtype)

建立等差陣列 — 指定步長
參數
- step:步長,預設值爲1

np.arange(10, 50, 2)

返回結果：

array([10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30, 32, 34, 36, 38, 40, 42,
       44, 46, 48])

1.3.3 np.logspace(start,stop, num)

建立等比數列
參數:
- num:要生成的等比數列數量，預設爲50

# 生成10^x
np.logspace(0, 2, 3)

返回結果:

array([  1.,  10., 100.])

1.4 生成亂數組

1.4.1 使用模組介紹

np.random模組

1.4.2 正態分佈

一、基礎概念複習：正態分佈（理解）

a. 什麼是正態分佈

正態分佈是一種概率分佈。正態分佈是具有兩個參數μ和σ的連續型隨機變數的分佈，第一參數μ是服從正態分佈的隨機變數的均值，第二個參數σ是此隨機變數的方差，所以正態分佈記作N(μ，σ )。

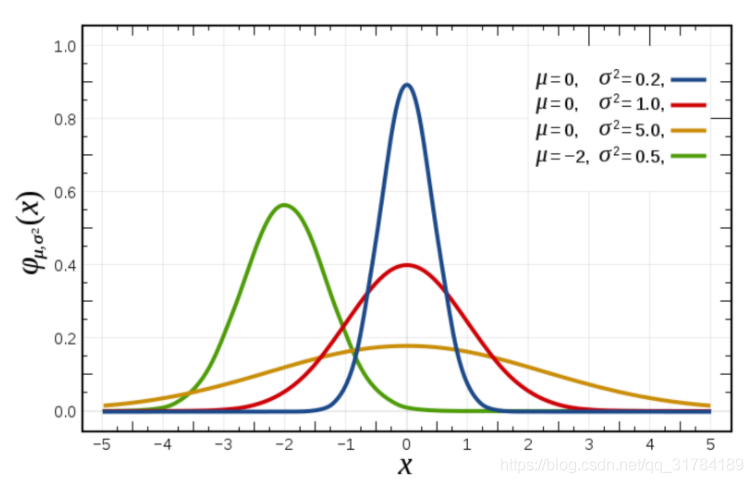
b. 正態分佈的應用

生活、生產與科學實驗中很多隨機變數的概率分佈都可以近似地用正態分佈來描述。

c. 正態分佈特點

μ決定了其位置，其標準差σ決定了分佈的幅度。當μ = 0,σ = 1時的正態分佈是標準正態分佈。

標準差如何來？

方差

是在概率論和統計方差衡量一組數據時離散程度的度量

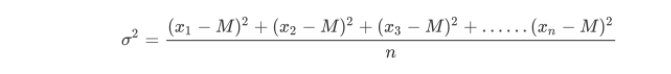
其中M爲平均值，n爲數據總個數，σ 爲標準差，σ ^2可以理解一個整體爲方差

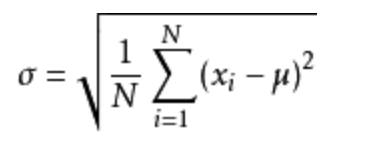
標準差與方差的意義

可以理解成數據的一個離散程度的衡量

二、正態分佈建立方式

np.random.randn(d0, d1, …, dn)

功能：從標準正態分佈中返回一個或多個樣本值
np.random.normal(loc=0.0, scale=1.0, size=None)

loc：float

此概率分佈的均值（對應着整個分佈的中心centre）

scale：float

此概率分佈的標準差（對應於分佈的寬度，scale越大越矮胖，scale越小，越瘦高）

size：int or tuple of ints

輸出的shape，預設爲None，只輸出一個值
np.random.standard_normal(size=None)

返回指定形狀的標準正態分佈的陣列。

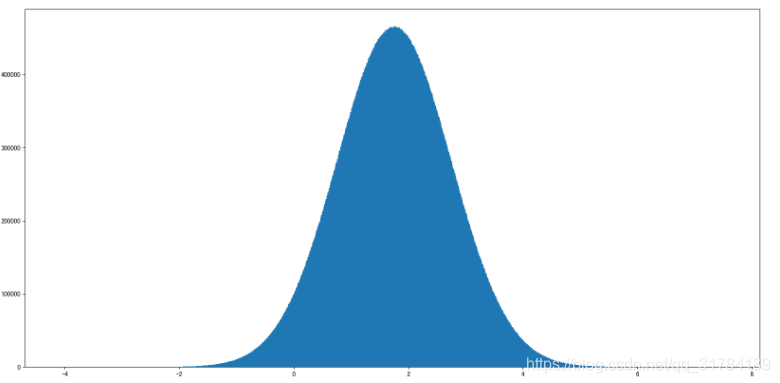
舉例1：生成均值爲1.75，標準差爲1的正態分佈數據，100000000個

x1 = np.random.normal(1.75, 1, 100000000)

返回結果：

array([2.90646763, 1.46737886, 2.21799024, ..., 1.56047411, 1.87969135,
       0.9028096 ])

# 生成均勻分佈的亂數
x1 = np.random.normal(1.75, 1, 100000000)

# 畫圖看分佈狀況
# 1）建立畫布
plt.figure(figsize=(20, 10), dpi=100)

# 2）繪製直方圖
plt.hist(x1, 1000)

# 3）顯示影象
plt.show()

例如：我們可以模擬生成一組股票的漲跌幅的數據

舉例2：隨機生成4支股票1周的交易日漲幅數據

4支股票，一週(5天)的漲跌幅數據，如何獲取？

隨機生成漲跌幅在某個正態分佈內，比如均值0，方差1

股票漲跌幅數據的建立

# 建立符合正態分佈的4只股票5天的漲跌幅數據
stock_change = np.random.normal(0, 1, (4, 5))
stock_change

返回結果：

array([[ 0.0476585 ,  0.32421568,  1.50062162,  0.48230497, -0.59998822],
       [-1.92160851,  2.20430374, -0.56996263, -1.44236548,  0.0165062 ],
       [-0.55710486, -0.18726488, -0.39972172,  0.08580347, -1.82842225],
       [-1.22384505, -0.33199305,  0.23308845, -1.20473702, -0.31753223]])

1.4.2 均勻分佈

np.random.rand(d0, d1, ..., dn)
- 返回[0.0，1.0)內的一組均勻分佈的數。
np.random.uniform(low=0.0, high=1.0, size=None)
- 功能：從一個均勻分佈[low,high)中隨機採樣，注意定義域是左閉右開，即包含low，不包含high.
- 參數介紹:
  - low: 採樣下界，float型別，預設值爲0；
  - high: 採樣上界，float型別，預設值爲1；
  - size: 輸出樣本數目，爲int或元組(tuple)型別，例如，size=(m,n,k), 則輸出mnk個樣本，預設時輸出1個值。
- 返回值：ndarray型別，其形狀和參數size中描述一致。
np.random.randint(low, high=None, size=None, dtype='l')
- 從一個均勻分佈中隨機採樣，生成一個整數或N維整數陣列，
- 取數範圍：若high不爲None時，取[low,high)之間隨機整數，否則取值[0,low)之間隨機整數。

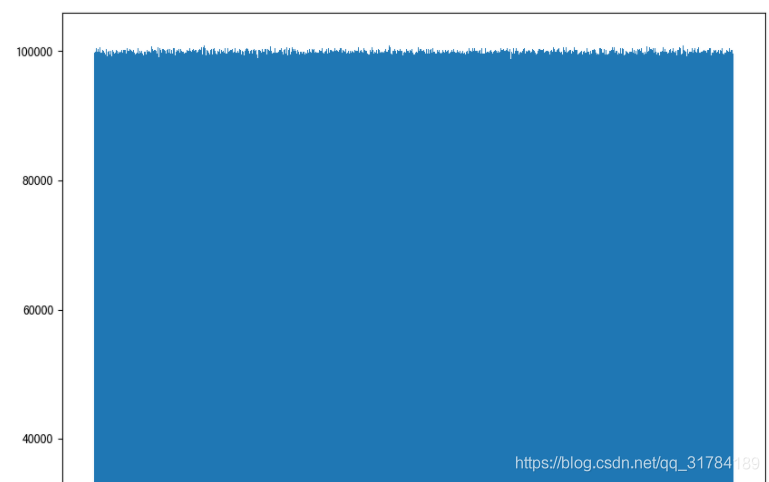
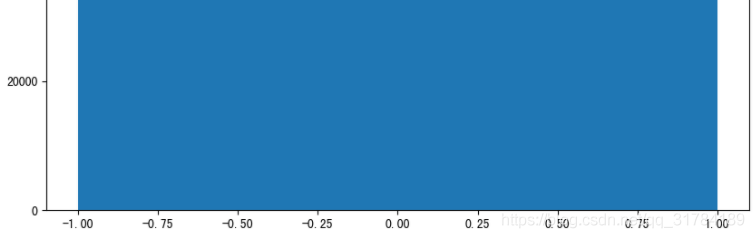
# 生成均勻分佈的亂數
x2 = np.random.uniform(-1, 1, 100000000)

返回結果：

array([ 0.22411206,  0.31414671,  0.85655613, ..., -0.92972446,
0.95985223,  0.23197723])

畫圖看分佈狀況：

import matplotlib.pyplot as plt

# 生成均勻分佈的亂數
x2 = np.random.uniform(-1, 1, 100000000)

# 畫圖看分佈狀況
# 1）建立畫布
plt.figure(figsize=(10, 10), dpi=100)

# 2）繪製直方圖
plt.hist(x=x2, bins=1000)  # x代表要使用的數據，bins表示要劃分割區間數

# 3）顯示影象
plt.show()

2 陣列的索引、切片

一維、二維、三維的陣列如何索引？

直接進行索引,切片
物件[:, :] -- 先行後列

二維陣列索引方式：

舉例：獲取第一個股票的前3個交易日的漲跌幅數據

# 二維的陣列，兩個維度 
stock_change[0, 0:3]

返回結果：

array([-0.03862668, -1.46128096, -0.75596237])

三維陣列索引方式：

# 三維
a1 = np.array([ [[1,2,3],[4,5,6]], [[12,3,34],[5,6,7]]])
# 返回結果
array([[[ 1,  2,  3],
        [ 4,  5,  6]],

       [[12,  3, 34],
        [ 5,  6,  7]]])
# 索引、切片
>>> a1[0, 0, 1]   # 輸出: 2

3 形狀修改

3.1 ndarray.reshape(shape, order)

返回一個具有相同數據域，但shape不一樣的檢視
行、列不進行互換

# 在轉換形狀的時候，一定要注意陣列的元素匹配
stock_change.reshape([5, 4])
stock_change.reshape([-1,10])  # 陣列的形狀被修改爲: (2, 10), -1: 表示通過待計算

3.2 ndarray.resize(new_shape)

修改陣列本身的形狀（需要保持元素個數前後相同）
行、列不進行互換

stock_change.resize([5, 4])

# 檢視修改後結果
stock_change.shape
(5, 4)

3.3 ndarray.T

陣列的轉置
將陣列的行、列進行互換

stock_change.T.shape
(4, 5)

4 型別修改

4.1 ndarray.astype(type)

返回修改了型別之後的陣列

stock_change.astype(np.int32)

4.2 ndarray.tostring([order])或者ndarray.tobytes([order])

構造包含陣列中原始數據位元組的Python位元組

arr = np.array([[[1, 2, 3], [4, 5, 6]], [[12, 3, 34], [5, 6, 7]]])
arr.tostring()

4.3 jupyter輸出太大可能導致崩潰問題【瞭解】

如果遇到

IOPub data rate exceeded.
    The notebook server will temporarily stop sending output
    to the client in order to avoid crashing it.
    To change this limit, set the config variable
    `--NotebookApp.iopub_data_rate_limit`.

這個問題是在jupyer當中對輸出的位元組數有限制，需要去修改組態檔

建立組態檔

jupyter notebook --generate-config
vi ~/.jupyter/jupyter_notebook_config.py

取消註釋,多增加

## (bytes/sec) Maximum rate at which messages can be sent on iopub before they
#  are limited.
c.NotebookApp.iopub_data_rate_limit = 10000000

但是不建議這樣去修改，jupyter輸出太大會崩潰

5 陣列的去重

5.1 np.unique()

temp = np.array([[1, 2, 3, 4],[3, 4, 5, 6]])
>>> np.unique(temp)
array([1, 2, 3, 4, 5, 6])

6 小結

建立陣列【掌握】
- 生成0和1的陣列
  - np.ones()
  - np.ones_like()
- 從現有陣列中生成
  - np.array -- 深拷貝
  - np.asarray -- 淺拷貝
- 生成固定範圍陣列
  - np.linspace()
    - nun -- 生成等間隔的多少個
  - np.arange()
    - step -- 每間隔多少生成數據
  - np.logspace()
    - 生成以10的N次冪的數據
- 生層亂數組
  - 正態分佈
    - 裏面需要關注的參數:均值:u, 標準差:σ
      - u -- 決定了這個圖形的左右位置
      - σ -- 決定了這個圖形是瘦高還是矮胖
    - np.random.randn()
    - np.random.normal(0, 1, 100)
  - 均勻
    - np.random.rand()
    - np.random.uniform(0, 1, 100)
    - np.random.randint(0, 10, 10)
陣列索引【知道】
- 直接進行索引,切片
- 物件[:, :] -- 先行後列
陣列形狀改變【掌握】
- 物件.reshape()
  - 沒有進行行列互換,新產生一個ndarray
- 物件.resize()
  - 沒有進行行列互換,修改原來的ndarray
- 物件.T
  - 進行了行列互換
陣列去重【知道】
- np.unique(物件)

============================================

4.4 ndarray運算

學習目標

目標
- 應用陣列的通用判斷函數
- 應用np.where實現陣列的三元運算

問題

如果想要操作符合某一條件的數據，應該怎麼做？

1 邏輯運算

# 生成10名同學，5門功課的數據
>>> score = np.random.randint(40, 100, (10, 5))

# 取出最後4名同學的成績，用於邏輯判斷
>>> test_score = score[6:, 0:5]

# 邏輯判斷, 如果成績大於60就標記爲True 否則爲False
>>> test_score > 60
array([[ True,  True,  True, False,  True],
       [ True,  True,  True, False,  True],
       [ True,  True, False, False,  True],
       [False,  True,  True,  True,  True]])

# BOOL賦值, 將滿足條件的設定爲指定的值-布爾索引
>>> test_score[test_score > 60] = 1
>>> test_score
array([[ 1,  1,  1, 52,  1],
       [ 1,  1,  1, 59,  1],
       [ 1,  1, 44, 44,  1],
       [59,  1,  1,  1,  1]])

2 通用判斷函數

np.all()

# 判斷前兩名同學的成績[0:2, :]是否全及格
>>> np.all(score[0:2, :] > 60)
False

np.any()

# 判斷前兩名同學的成績[0:2, :]是否有大於90分的
>>> np.any(score[0:2, :] > 80)
True

3 np.where（三元運算子）

通過使用np.where能夠進行更加複雜的運算

np.where()

# 判斷前四名學生,前四門課程中，成績中大於60的置爲1，否則爲0
temp = score[:4, :4]
np.where(temp > 60, 1, 0)

複合邏輯需要結合np.logical_and和np.logical_or使用

# 判斷前四名學生,前四門課程中，成績中大於60且小於90的換爲1，否則爲0
np.where(np.logical_and(temp > 60, temp < 90), 1, 0)

# 判斷前四名學生,前四門課程中，成績中大於90或小於60的換爲1，否則爲0
np.where(np.logical_or(temp > 90, temp < 60), 1, 0)

4 統計運算

如果想要知道學生成績最大的分數，或者做小分數應該怎麼做？

4.1 統計指標

在數據挖掘/機器學習領域，統計指標的值也是我們分析問題的一種方式。常用的指標如下：

min(a, axis)
- Return the minimum of an array or minimum along an axis.
max(a, axis])
- Return the maximum of an array or maximum along an axis.
median(a, axis)
- Compute the median along the specified axis.
mean(a, axis, dtype)
- Compute the arithmetic mean along the specified axis.
std(a, axis, dtype)
- Compute the standard deviation along the specified axis.
var(a, axis, dtype)
- Compute the variance along the specified axis.

4.2 案例：學生成績統計運算

進行統計的時候，axis 軸的取值並不一定，Numpy中不同的API軸的值都不一樣，在這裏，axis 0代表列, axis 1代錶行去進行統計

# 接下來對於前四名學生,進行一些統計運算
# 指定列 去統計
temp = score[:4, 0:5]
print("前四名學生,各科成績的最大分：{}".format(np.max(temp, axis=0)))
print("前四名學生,各科成績的最小分：{}".format(np.min(temp, axis=0)))
print("前四名學生,各科成績波動情況：{}".format(np.std(temp, axis=0)))
print("前四名學生,各科成績的平均分：{}".format(np.mean(temp, axis=0)))

結果：

前四名學生,各科成績的最大分：[96 97 72 98 89]
前四名學生,各科成績的最小分：[55 57 45 76 77]
前四名學生,各科成績波動情況：[16.25576821 14.92271758 10.40432602  8.0311892   4.32290412]
前四名學生,各科成績的平均分：[78.5  75.75 62.5  85.   82.25]

如果需要統計出某科最高分對應的是哪個同學？

np.argmax(temp, axis=)
np.argmin(temp, axis=)

print("前四名學生，各科成績最高分對應的學生下標：{}".format(np.argmax(temp, axis=0)))

結果：

前四名學生，各科成績最高分對應的學生下標：[0 2 0 0 1]

5 小結

邏輯運算【知道】
- 直接進行大於,小於的判斷
- 合適之後,可以直接進行賦值
通用判斷函數【知道】
- np.all()
- np.any()
統計運算【掌握】
- np.max()
- np.min()
- np.median()
- np.mean()
- np.std()
- np.var()
- np.argmax(axis=) — 最大元素對應的下標
- np.argmin(axis=) — 最小元素對應的下標

==========================================

4.5 陣列間運算

學習目標

目標
- 知道陣列與數之間的運算
- 知道陣列與陣列之間的運算
- 說明陣列間運算的廣播機制機製

1 陣列與數的運算

arr = np.array([[1, 2, 3, 2, 1, 4], [5, 6, 1, 2, 3, 1]])
arr + 1
arr / 2

# 可以對比python列表的運算，看出區別
a = [1, 2, 3, 4, 5]
a * 3

2 陣列與陣列的運算

arr1 = np.array([[1, 2, 3, 2, 1, 4], [5, 6, 1, 2, 3, 1]])
arr2 = np.array([[1, 2, 3, 4], [3, 4, 5, 6]])

上面這個能進行運算嗎，結果是不行的！

2.1 廣播機制機製

陣列在進行向量化運算時，要求陣列的形狀是相等的。當形狀不相等的陣列執行算術運算的時候，就會出現廣播機制機製，該機制機製會對陣列進行擴充套件，使陣列的shape屬性值一樣，這樣，就可以進行向量化運算了。下面下麪通過一個例子進行說明：

arr1 = np.array([[0],[1],[2],[3]])
arr1.shape
# (4, 1)

arr2 = np.array([1,2,3])
arr2.shape
# (3,)

arr1+arr2
# 結果是：
array([[1, 2, 3],
       [2, 3, 4],
       [3, 4, 5],
       [4, 5, 6]])

上述程式碼中，陣列arr1是4行1列，arr2是1行3列。這兩個陣列要進行相加，按照廣播機制機製會對陣列arr1和arr2都進行擴充套件，使得陣列arr1和arr2都變成4行3列。

下面下麪通過一張圖來描述廣播機制機製擴充套件陣列的過程：

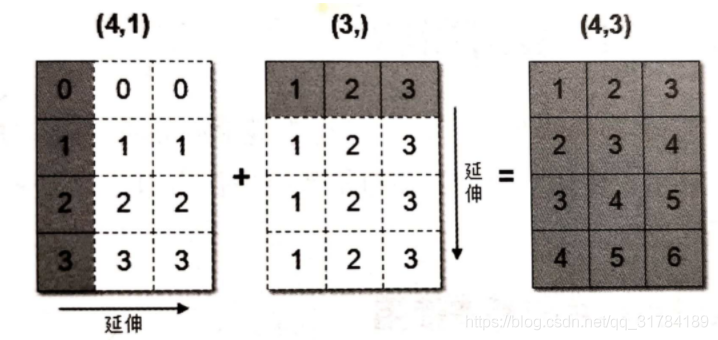
廣播機制機製實現了時兩個或兩個以上陣列的運算，即使這些陣列的shape不是完全相同的，只需要滿足如下任意一個條件即可。

1.陣列的某一維度等長。
2.其中一個數組的某一維度爲1 。

廣播機制機製需要擴充套件維度小的陣列，使得它與維度最大的陣列的shape值相同，以便使用元素級函數或者運算子進行運算。

如果是下面下麪這樣，則不匹配：

A  (1d array): 10
B  (1d array): 12
A  (2d array):      2 x 1
B  (3d array):  8 x 4 x 3

思考：下面下麪兩個ndarray是否能夠進行運算？

arr1 = np.array([[1, 2, 3, 2, 1, 4], [5, 6, 1, 2, 3, 1]])
arr2 = np.array([[1], [3]])

3 小結

陣列運算,滿足廣播機制機製,就OK【知道】
- 1.維度相等
- 2.shape(其中對應的地方爲1,也是可以的)

================================================

4.6 數學：矩陣

學習目標

目標
- 知道什麼是矩陣和向量
- 知道矩陣的加法,乘法
- 知道矩陣的逆和轉置
- 應用np.matmul、np.dot實現矩陣運算

1 矩陣和向量

1.1 矩陣

矩陣，英文matrix，和array的區別矩陣必須是2維的，但是array可以是多維的。

如圖:這個是 3×2 矩陣，即 3 行 2 列，如 m 爲行，n 爲列，那麼 m×n 即 3×2

矩陣的維數即行數×列數

矩陣元素(矩陣項):

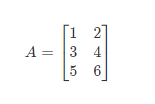
Aij 指第 i 行，第 j 列的元素。

1.2 向量

向量是一種特殊的矩陣，講義中的向量一般都是列向量，下面下麪展示的就是三維列向量(3×1)。)

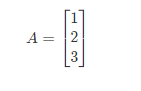
2 加法和標量乘法

矩陣的加法:行列數相等的可以加。

例:

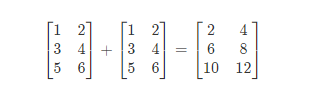
矩陣的乘法:每個元素都要乘。

例:

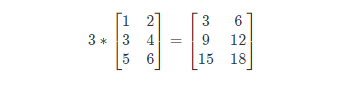
組合演算法也類似。

3 矩陣向量乘法

矩陣和向量的乘法如圖：m×n 的矩陣乘以 n×1 的向量，得到的是 m×1 的向量

例:

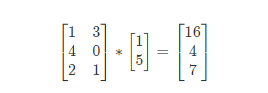
1*1+3*5 = 16
4*1+0*5 = 4
2*1+1*5 = 7

矩陣乘法遵循準則：

(M行, N列)*(N行, L列) = (M行, L列)

4 矩陣乘法

矩陣乘法：

m×n 矩陣乘以 n×o 矩陣，變成 m×o 矩陣。

舉例：比如說現在有兩個矩陣 A 和 B，那麼它們的乘積就可以表示爲圖中所示的形式。

練一練

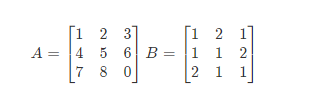
求矩陣AB的結果

答案：

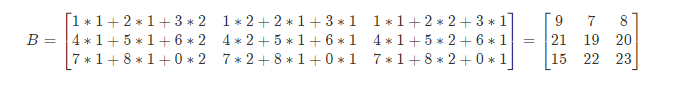
5 矩陣乘法的性質

矩陣的乘法不滿足交換律：A×B≠B×A

矩陣的乘法滿足結合律。即：A×（B×C）=（A×B）×C

單位矩陣：在矩陣的乘法中，有一種矩陣起着特殊的作用，如同數的乘法中的 1,我們稱這種矩陣爲單位矩陣．它是個方陣，一般用 I 或者 E 表示，從左上角到右下角的對角線（稱爲主對角線）上的元素均爲 1 以外全都爲 0。如：

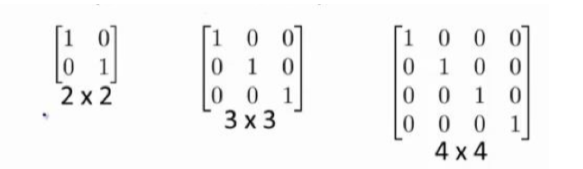
6 逆、轉置

矩陣的逆：如矩陣 A 是一個 m×m 矩陣（方陣），如果有逆矩陣，則：

低階矩陣求逆的方法:

1.待定係數法

2.初等變換

矩陣的轉置：設 A 爲 m×n 階矩陣（即 m 行 n 列），第 i 行 j 列的元素是 a(i,j)，即：

A=a(i,j)

定義 A 的轉置爲這樣一個 n×m 階矩陣 B，滿足 B=a(j,i)，即 b (i,j)=a (j,i)（B 的第 i 行第 j 列元素是 A 的第 j 行第 i 列元素），記 AT =B。

直觀來看，將 A 的所有元素繞着一條從第 1 行第 1 列元素出發的右下方 45 度的射線作鏡面反轉，即得到 A 的轉置。

例：

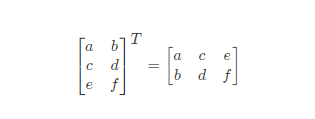
7 矩陣運算

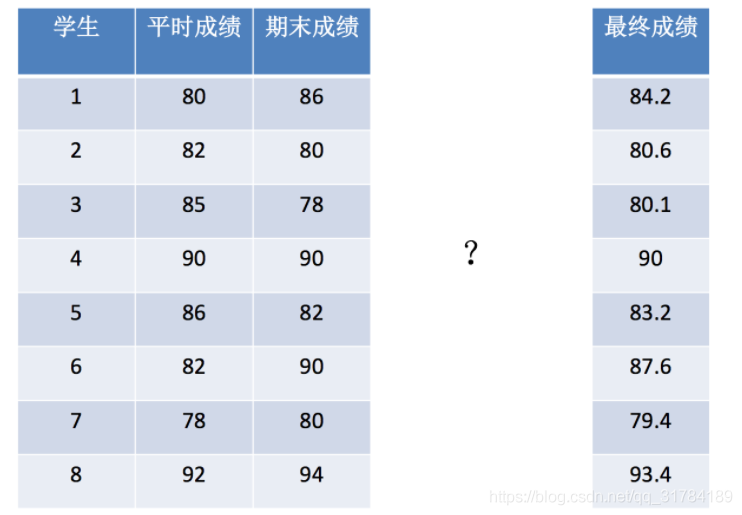
7.1 矩陣乘法api：

np.matmul
np.dot

>>> a = np.array([[80, 86],
[82, 80],
[85, 78],
[90, 90],
[86, 82],
[82, 90],
[78, 80],
[92, 94]])
>>> b = np.array([[0.7], [0.3]])

>>> np.matmul(a, b)
array([[81.8],
       [81.4],
       [82.9],
       [90. ],
       [84.8],
       [84.4],
       [78.6],
       [92.6]])

>>> np.dot(a,b)
array([[81.8],
       [81.4],
       [82.9],
       [90. ],
       [84.8],
       [84.4],
       [78.6],
       [92.6]])

np.matmul和np.dot的區別:

二者都是矩陣乘法。 np.matmul中禁止矩陣與標量的乘法。在向量乘向量的內積運算中，np.matmul與np.dot沒有區別。

7 小結

1.矩陣和向量【知道】
- 矩陣就是特殊的二維陣列
- 向量就是一行或者一列的數據
2.矩陣加法和標量乘法【知道】
- 矩陣的加法:行列數相等的可以加。
- 矩陣的乘法:每個元素都要乘。
3.矩陣和矩陣(向量)相乘【知道】
- (M行, N列)*(N行, L列) = (M行, L列)
4.矩陣性質【知道】
- 矩陣不滿足交換率,滿足結合律
5.單位矩陣【知道】
- 對角線都是1的矩陣,其他位置都爲0
6.矩陣運算【掌握】
- np.matmul
- np.dot
- 注意：二者都是矩陣乘法。 np.matmul中禁止矩陣與標量的乘法。在向量乘向量的內積運算中，np.matmul與np.dot沒有區別。

Python_機器學習_Numpy（4）

Numpy

學習目標

4.1 Numpy優勢

學習目標

1 Numpy介紹

2 ndarray介紹

3 ndarray與Python原生list運算效率對比

4 ndarray的優勢

5 小結

4.2 N維陣列-ndarray

學習目標

1 ndarray的屬性

2 ndarray的形狀

3 ndarray的型別

4 總結

4.3 基本操作

學習目標

1 生成陣列的方法

1.1 生成0和1的陣列

1.2 從現有陣列生成

1.3 生成固定範圍的陣列

1.4 生成亂數組

2 陣列的索引、切片

3 形狀修改

3.1 ndarray.reshape(shape, order)

3.2 ndarray.resize(new_shape)

3.3 ndarray.T

4 型別修改

4.1 ndarray.astype(type)

4.2 ndarray.tostring([order])或者ndarray.tobytes([order])

4.3 jupyter輸出太大可能導致崩潰問題【瞭解】

5 陣列的去重

5.1 np.unique()

6 小結

4.4 ndarray運算

學習目標

問題

1 邏輯運算

2 通用判斷函數

3 np.where（三元運算子）

4 統計運算

4.1 統計指標

4.2 案例：學生成績統計運算

5 小結

4.5 陣列間運算

學習目標

1 陣列與數的運算

2 陣列與陣列的運算

2.1 廣播機制 機製

3 小結

4.6 數學：矩陣

學習目標

1 矩陣和向量

1.1 矩陣

1.2 向量

2 加法和標量乘法

3 矩陣向量乘法

4 矩陣乘法

5 矩陣乘法的性質

6 逆、轉置

7 矩陣運算

7.1 矩陣乘法api：

7 小結

2.1 廣播機制機製