技術文章 » 【路徑追蹤】前置知識1--輻射度測量學 Radiometry

【路徑追蹤】前置知識1--輻射度測量學 Radiometry

2020-08-13 21:06:28

Intro

什麼是輻射度測量學? 爲什麼需要輻射度測量學?
輻射度測量學爲我們提供了用於描述光線傳播和反射的相關概念以及數學工具.
圖學早期, 在各種條件的制約下, 我們一般通過諸如 Lambert 漫反射模型、Blinn-Phong 高光模型等計算表面光照. 這些經驗模型能在一定程度上滿足了人們對效率和效果的需求, 但是與產生令人信服的真實感渲染結果依舊存在較大的差距.
輻射度測量學就是用來解決這一問題的工具. 輻射度測量學通過精準表達光學的物理資訊, 讓我們得以在物理正確的基礎上進行與光照相關的計算, 從而得到物理正確的結果.

光線追蹤系統中對輻射度測量學的基本假設

雖然輻射度測量學是物理正確的, 但對於圖學來說, 我們只在集合光學領域進行計算. 在相關的討論中都隱含着如下假設:

  1. 線性 Linearity: 光學系統中兩個輸入的合成效果通常等價於各自輸入之和. 這一特性十分重要, 線性可加性極大的簡化了我們對光線傳輸的分析與計算
  2. 能量守恆 Energy conservation
  3. 忽略偏振現象 No polarization
  4. 忽略熒光或磷光現象 No fluorescence or Phosphorescence
  5. 穩態 Steady state: 假設光線在環境中已經達到了穩定的狀態, 所以 radiance 的分佈不會隨着時間的變化而變化. (在現實中光線的穩態往往在瞬間完成, 所以這一假設並不是系統產生的限制條件)

PS: 在這些條件下, 依舊難以有效表示的現象是光線的幹涉和衍射現象. 產生這些現象的時候, 兩片區域的全部 FLux 並不等於各自區域 Flux 的和.

輻射度測量學中的關鍵物理量

1. Radiant Energy
2. Flux(Power)
3. Intensity
4. Irradiance
5. Radiance

Radiant Energy

能量是輻射度測量學的起點, 單位是焦耳. 由於能量會隨着時間不斷累積, 所以在圖學領域很少使用能量進行研究, 但是我們需要使用的物理量都是由能量開始不斷計算得出的.
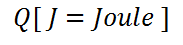
Energy

Flux(Power)

Flux表示單位時間內輻射出的能量, Flux也被稱爲功率(Power).
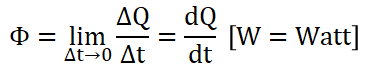
Power
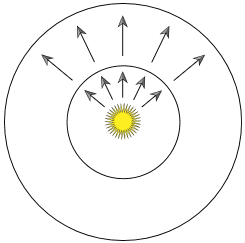
在渲染時, 我們一般用 Flux 來表示光源的總髮射量. 以點光源爲例, 我們通過設定包圍點光源的球殼來分析 Flux. 需要注意的是, 雖然大球殼上通過任何一個微面元的能量都小於小球殼上的, 但是由於大球殼同時擁有更大的表面積, 所以大小兩個球殼上的總 Flux 是相等的.

Point Light

衡量光源資訊的重要物理量

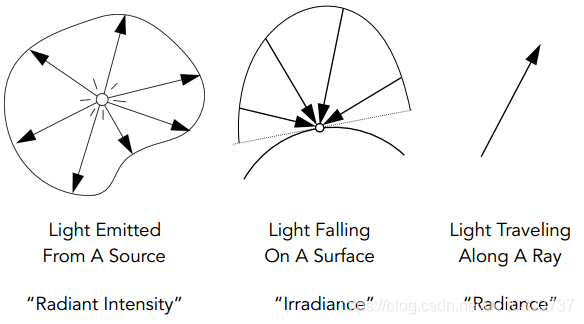
Radiance

  • Intensity : 定義光源輻射出多少能量
  • Irradiance : 定義物體表面可以接收到多少能量
  • Radiance : 定義光線在傳播時的能量

Intensity

Intensity 表示單位立體角(Solid Angle)上光源輻射的 power.
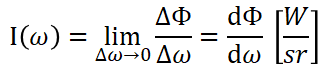
Intensity

那麼什麼是立體角? 我們知道平面上的一個角等於其對應的弧長除以半徑. 立體角也採用非常類似的定義方式, 我們從球心發射一個類錐體會在球面上擷取出一個面積, 立體角就等於這個面積除以半徑的平方(注意! 我們所說的面積是在球面上的投影面積).
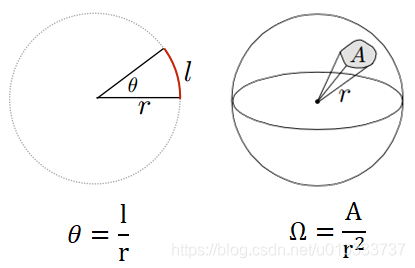角和立体角下圖展示了微分立體角, 計算非常直觀不再贅述.

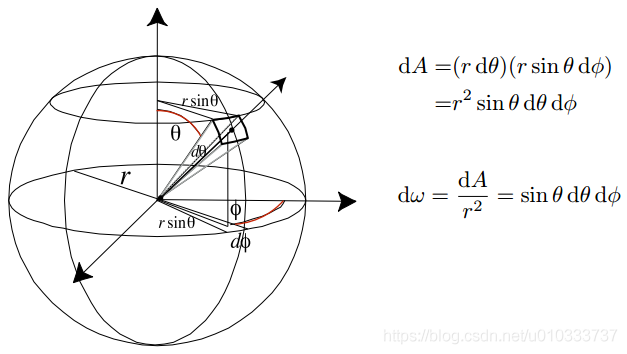
微分立体角

Irradiance

Irradiance 表示物體表面上單位面積上接收到的 power.

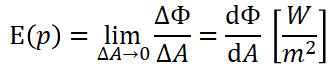
Irradiance

如下圖所示, Irradiance 的定義同時也解釋了 Lambert Cosine Law 的含義.
(Lambert Cosine Law : 到達物體表面的光能與光線方向和表面法線夾角的餘弦成正比)

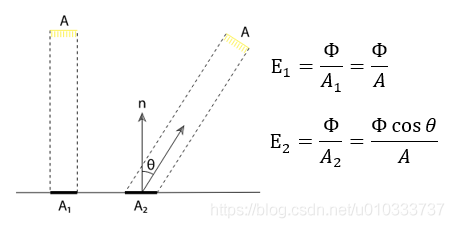
Lambert Cosine Law
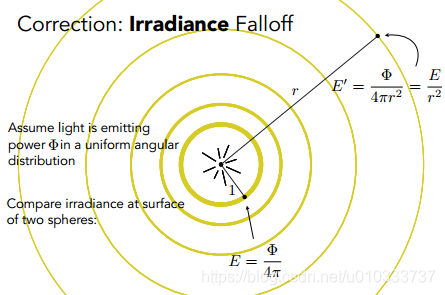
與之類似, 我們同樣可以直接利用 Irradiance 的定義來解釋爲什麼點光源會以距離平方的形式不斷衰減. 同時這裏我們可以進一步明確一點, 我們所說的衰減, 是 Irradiance 在衰減, Intensity 並不會衰減.

点光衰减

Radiance

Irradiance 告訴了我們表面上單位面積內接收到的 power 是多少. 這其中有一個關鍵的問題是 Irradiance 並沒有體現出 power 在不同方向上的分佈, 而光線追蹤的過程明顯是與方向相關的, 所以我們定義了 Radiance 來表達這一屬性.
Radiance 是指輻射源在某一方向, 每單位投影面積, 每單位立體角內的 power.
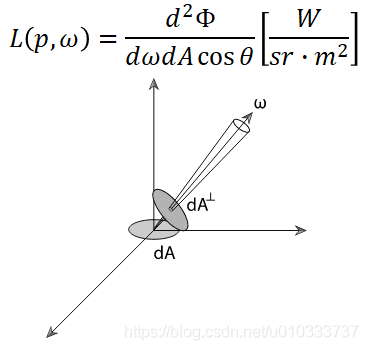Radiance接下來我們嘗試使用"傳輸理論"來解釋 Radiance 定義中的餘弦項從何而來.
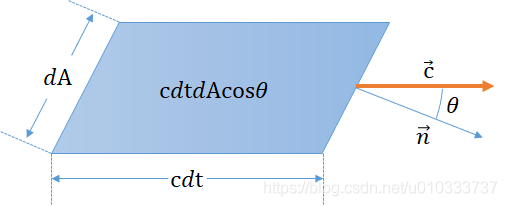
傳輸理論涉及物理量(如能量, 電荷, 品質)的傳輸或流動. 假設我們已知 x 處的光粒子密度爲 p(x), 那麼在一個很小的體積 dV 內光粒子的個數就是 p(x)dV. 下面 下麪再考慮這些粒子在時間 dt 內穿過一些不同的表面 dA. 假設光粒子的速度爲 c, 那麼這段時間內流過表面的體積就是 cdtdAcosθ, 那麼穿過表面的粒子數量就是 p(x)cdtdAcosθ. 這很直觀的說明了我們爲什麼要使用投影面積以及 radiance 中餘弦項的來源.

传输理论

參考資料