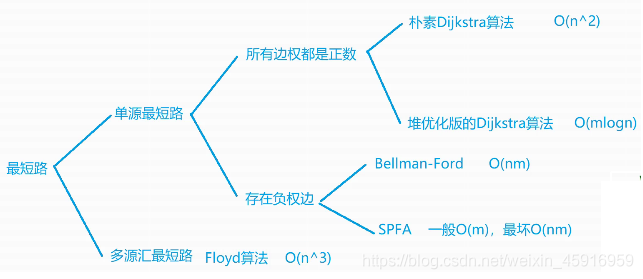
最短路

樸素Dijkstra

1、思路
*0、定義陣列 dis[n] (從1到其它點的距離）, s[n](已經確定最短距離的點）；
*1、初始化 dis[1] = 0, dis[其它點] = 正無窮；
*2、 for(1 ~ n);——————————回圈 n 次,更新所有的點 t；
*3 找到 不在s中的，距離最近的點 t；
*4 將t加入s;
*5 用t更新其它點的距離;————————回圈n次
（這裏是兩 層 回圈， 所以時間複雜度是 n^2）
*6 返回

例題

#include<bits/stdc++.h>
using namespace std;
const int N = 510;

int n, m;
int g[N][N];
int djs[N];
bool s[N];

int djst(){
    memset(djs, 0x3f3f3f3f, sizeof djs);/* *1 */
    djs[1] = 0;							/* *1 */
    
    for(int i = 0; i < n; i ++){		/* *2 */
        int t = -1;										/* *3 */
        for(int j = 1; j <= n; j ++)					/* *3 */
            if(!s[j] && (t == -1 || djs[t] > djs[j]))	/* *3 */ 
                t = j;									/* *3 */
            
        s[t] = 1;										/* *4 */
        
        for(int j = 1; j <= n; j ++)					/* *5 */
            djs[j] = min(djs[j], djs[t] + g[t][j]);		/* *5 */
    }
    if(djs[n] == 0x3f3f3f3f) return -1;					/* *6 */
    return djs[n];										/* *6 */
}

int main(){
    cin >> n >> m;
    memset(g, 0x3f3f3f3f, sizeof g);
    while(m --){
        int a, b, c;
        cin >> a >>b >>c;
        g[a][b] = min(g[a][b], c);
    }
    int t = djst();
    
    cout << t;
    
    return 0;
}
/*
0x3f3f3f3f 代表 正無窮。
*/

優化Dijkstra ：

可以更新的地方：
分析：


*2、 for(1 ~ n);·；
*3	找到 不在s中的，距離最近的點 t；——————*2、*3共回圈 n^2 次來找點 t;（用堆來做可時間O(n)）
*4	將t加入s;——————————————————這裏是n次
*5	用t更新其它點的距離;—————————————具體操作時m次嗎,遍歷所有的邊來更新
堆優化後 整個計算量最大是 O(m log n）。
堆的寫法：
手寫或用優先佇列，兩者時間是一個級別的，用優先佇列，不需要手寫堆。

#include<bits/stdc++.h>
using namespace std;
const int N = 150010;

int n, m;
int djs[N];
bool st[N];
int ne[N], e[N], h[N], w[N], idx = 0;

typedef pair<int ,int> P;

void add(int a, int b, int c){
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++;
}

int djst(){
    memset(djs, 0x3f, sizeof djs);
    djs[1] = 0;
    
    priority_queue< P, vector<P>, greater<P> > heap;/* *1 */
    heap.push( {0, 1} );
    
    while(heap.size()){
        auto t = heap.top();
        heap.pop();
        
        int ver = t.second, distance = t.first;
        if(st[ver]) continue;
        
        st[ver] = 1;								/* *2 */
        
        for(int i = h[ver]; i != -1; i = ne[i]){
            int j = e[i];
            if(djs[j] > distance + w[i]){
                djs[j] = distance + w[i];
                heap.push({djs[j], j});
            }
        }
    }       
   
    if(djs[n] == 0x3f3f3f3f) return -1;
    return djs[n];
}

int main(){
    cin >> n >> m;
    memset(h, -1, sizeof h);
    while(m --){
        int a, b, c;
        cin >> a >>b >>c;
        add(a, b, c);
    }
    cout << djst() << endl;
    return 0;
}

給定一個n個點m條邊的有向圖，圖中可能存在重邊和自環，所有邊權均爲非負值。

請你求出1號點到n號點的最短距離，如果無法從1號點走到n號點，則輸出-1。

輸入格式
第一行包含整數n和m。

接下來m行每行包含三個整數x，y，z，表示存在一條從點x到點y的有向邊，邊長爲z。

輸出格式
輸出一個整數，表示1號點到n號點的最短距離。

如果路徑不存在，則輸出-1。

數據範圍
1≤n,m≤1.5×105,
圖中涉及邊長均不小於0，且不超過10000。

輸入樣例：
3 3
1 2 2
2 3 1
1 3 4
輸出樣例：
3
*1 強調：「>」不要兩個拼在一起。
less是從大到小，greater是從小到大。
第一個參數爲數據型別。
第二個參數爲容器型別。
第三個參數爲比較函數。
*2 千萬不要忘記。