概念

生成樹：一個連通圖含有全部$n$個頂點，但只有足以構成一棵樹的$n-1$條邊。一顆n個頂點的生成樹有且僅有$n-1$條邊，如果生成樹當中再新增一條邊，必定成環。
最小生成樹($MST$)：在聯通網中的所有生成樹中，所有邊代價最小的生成樹，成爲最小生成樹。

prim

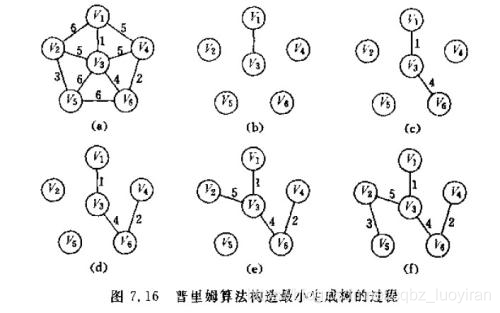
原理：從起點頂點開始，選擇當前可用的最小權值和，把對應的頂點加入到當前建立的生成樹當中。
令初始狀態爲$u$，所有頂點結合爲$V$，當前剩餘沒用的頂點集合爲$v$。
1.初始化：$u={s},v=V-u$
2.找出一條連線集合$u$和$v$的最小代價的邊$(u0,v0)$,把他連起來，並將$v0$加入到$u$中，修改相關的值。
3.重複操作2，直到所有頂點都被連上。

程式碼：

#define MAXN 1000
#define INF 1<<30
int closest[MAXN],lowcost[MAXN],m;//m爲節點的個數
int G[MAXN][MAXN];//鄰接矩陣
int prim()
	{
	for(int i=0;i<m;i++)
	{
		lowcost[i]=INF;
	}
	for(int i=0;i<m;i++)
	{
		closest[i]=0;
	}
	closest[0]=-1;//加入第一個點，-1表示該點在集合U中，否則在集合V中
	int num=0,ans=0,e=0;//e爲最新加入集合的點
	while(num<m-1)//加入m-1條邊
	{
		int micost=INF,miedge=-1;
		for(int i=0;i<m;i++)
		if(closest[i]!=-1)
		{
		int temp=G[e][i];
		if(temp<lowcost[i])
		{
		lowcost[i]=temp;
		closest[i]=e;
		}
		if(lowcost[i]<micost)
		micost=lowcost[miedge=i];
		}
		ans+=micost;
		closest[e=miedge]=-1;
		num++;
	}
	return ans;
}

kruskal演算法

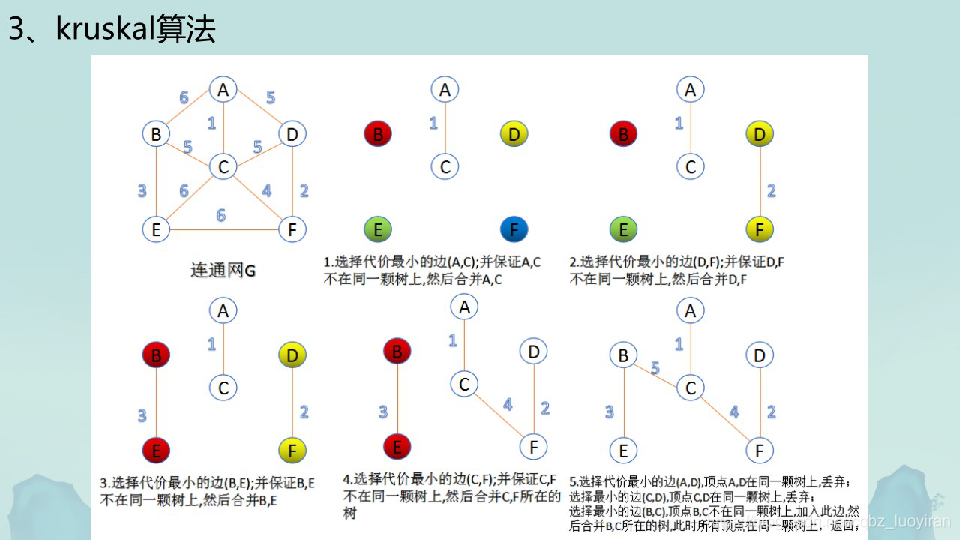
原理：從邊出發，初始狀態下最小生成樹選取0條邊，在計算過程中，每次新增一條滿足條件的邊進入最小生成樹中，知道選完爲止。
步驟：
1.把邊從小到大排序
2.並查集判斷祖先
3.加邊，重複2操作

程式碼：

int kruskal() {
	sort(c + 1,c + k + 1);
	for(int i = 1;i <= n;i ++)
	fa[i] = i;
	for(int i = 1;i <= k;i ++) {
		int x = Find_Set(c[i].u);
		int y = Find_Set(c[i].v);
		if(x == y)
		continue;
		fa[x] = y;
		ans += c[i].w;
	}
}