最近在知乎上看到了一個話題：世界上有哪些程式碼量很少，但很牛逼很經典的演算法或專案案例？其中有一個回答是雷神之錘3中的快速逆平方根演算法，我本以爲是電影中雷神3中出現的程式碼，就特別好奇點進去看了一下，結果真是對應了程式碼註釋中的一句話「what the fuck?」。

越不會越好奇，查過之後才知道這是一款遊戲中的部分程式碼，1999年發佈，2005年開源，距離現在已經有20年了，據說這部分程式碼出現在公共場合時，幾乎震住了所有人，也就是下面 下麪這幾行程式碼：

float Q_rsqrt( float number )
{
  long i;
  float x2, y;   #公衆號【測試員小何】
  const float threehalfs = 1.5f;
  x2 = number * 0.5f;
  y  = number;
  i  = * ( long * ) &y;  // evil floating point bit level hacking
  i  = 0x5f3759df - ( i >> 1 ); // what the fuck?
  y  = * ( float * ) &i;
  y  = y * ( threehalfs - ( x2 * y * y ) ); // 1st iteration
  // y  = y * ( threehalfs - ( x2 * y * y ) ); // 2nd iteration, this can be removed
  return y;
}

可能很多程式設計師老手都知道這段牛B的程式碼，但對於很多人應該是空白的。求一個數的平方根我們通常會用到庫中的內建方法，也就是sqrt，比如C語言中求一個數的平方根倒數，利用float(1.0/sqrt(x))即可。

可能那個時候沒有sqrt方法，作者被「被逼無奈」想到了這種方法，但是最牛逼的是這種方法要比sqrt方法快的多，據說在有的CPU上可以快4倍，也有說快20%的，但我的電腦上編譯是要快接近30%，而快的很大原因之一是因爲程式碼中的一串神祕的數位0x5f3759df。下面 下麪結合一些相關知識和推導來介紹作者幾個騷操作，最終的目的都是爲了得到這個神祕數位。

首先我們要先明確一個基礎知識，即單精度浮點數在32位元中是如何儲存的。32bit可以共分爲三個部分S、E、M，其中S只有1位，0表示正數、1表示負數；E表示小數，共有8位元；M表示尾數，共有23位，如下圖：

以數位4.25爲例，整數4的二進制表示爲0100；與二進制表示整數同理，小數也是如此，比如202^020右側就是2−12^{-1}2−1，那麼4.25轉化爲二進制形式就是0100.01。將二進制形式轉用科學計數法的形式可以表示爲1.0001×22=(1+0.0001)×221.0001\times2^2=(1+0.0001)\times2^21.0001×22=(1+0.0001)×22。

這裏先用s、e、m表示，因爲S、E、M另有含義

由於4.25是正數，那麼s位就儲存爲0，然後可以將指數處的2+127以二進制形式儲存至e中，加上127的理由是將指數的範圍由(-127,128)移碼至(0,255)，這樣就可以用指數位置就不用考慮符號問題。最後將小數點後的0001儲存至m中，因爲後面的數足以確定小數點前爲1，所以沒有必要再儲存1，綜上就是一個單精度浮點數在32位元記憶體中的儲存方式，如下圖：

所以對於一個要開放的浮點數x，有以下表示形式，先暫稱爲儲存表達式(這個表達式下文需要用到)：

x=(−1)s+(1+m)×2ex = (-1)^s+(1+m)\times 2^ex=(−1)s+(1+m)×2e

雖然e和m表示的實際意義是浮點數，但是畢竟二進制是都可以轉換成十進制的整數嘛，那麼如果從整數的角度看，整數E和浮點數e、整數M和浮點數m有沒有某種關係呢？答案是肯定有的，但是理由呢我不知道=.=

E=127+eE = 127+eE=127+e

M=1019mM = 10^{19}mM=1019m

加127的原因上文已經介紹了，就是爲了調整指數的符號範圍；101910^{19}1019是m中1後所需補零的個數，因爲當從浮點數角度看時，1左邊的0是有起到佔位作用的，而如果從整數角度看時，1右邊的0纔有實際意義，所以在原基礎的m上乘以1後零個數的次冪就可以轉化至整M。

我們再回到最初的問題，對於一個浮點數x,求它的逆平方根：

y=1x√=x−12y = \frac{1}{\sqrt{x} \quad} = x^ {- \frac{1}{2}}y=x​1​=x−21​

如果對等式兩邊同時取對數：

log2y=−12log2xlog_2 y = - \frac{1}{2} log_2xlog2​y=−21​log2​x

如果結合上面的儲存表達式，又可以得到一個新的等式：

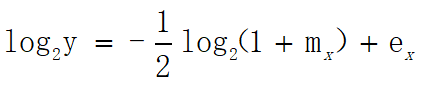
對於上式中的log2(1+mx)log_2(1+m_x)log2​(1+mx​)可以繪製出一條平滑的曲線，我們可以用直線y=mxy=m_xy=mx​對比(如下圖)，可以看到兩條線在(0,1)之間非常相近，那麼如果再將這條直線向上平移一點點，可以假設這個平移的距離爲b，那麼兩條線就有一種近似相等的關係：log2(1+mx)≈mx+blog_2(1+m_x)\approx m_x+blog2​(1+mx​)≈mx​+b。

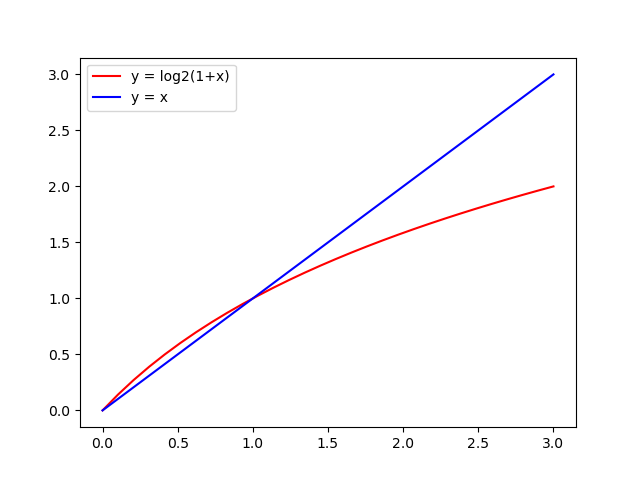
需要注意的是這種關係成立的前提是0≤mx≤10\leq m_x\leq 10≤mx​≤1，經代入得到下面 下麪式子：

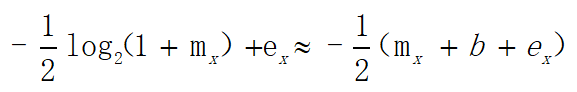
如果對log2ylog_2 ylog2​y做相同處理，那麼就有下面 下麪式子：

my+ey+b≈−12(mx+ex+b)m_y+e_y+b \approx -\frac{1}{2}(m_x+e_x+b)my​+ey​+b≈−21​(mx​+ex​+b)

上面我們不是利用整數型的M和E分別表示m和e嘛，那麼自然可以用整數型套用上式中的浮點型，對於不同數位，整數型和浮點型之間的關係也不同，所以這裏統一用常數B和L表示，如下：

E=B+eE = B+eE=B+e

M=LmM = LmM=Lm

用整數型替換浮點型可以得到新式子：

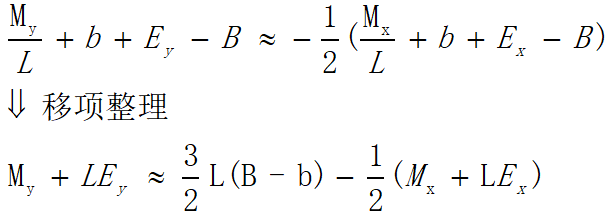
可以看到整理後的式子左右有一個相同的部分M+LEM+LEM+LE，我們已經知道了這三個字母代表的意思，但合在一起表達的又是一個新概念，合併兩個整數是一個很簡單的問題，比如合併33和55，33×100+55=335533\times100+55=335533×100+55=3355，那麼LE+MLE+MLE+M不就是這個道理嘛，只不過前者是十進制後者是二進制，所以LE+MLE+MLE+M的作用就是將M和E儲存的數位捆綁在一起，用來表示儲存的數位，有人想前面不是還有一位S嗎？S的作用是表示儲存數位的正負，根號下的數位一定爲正，所以S這位一定爲0，沒有實際意義。有沒有感覺真的秒！

既然這個組合用來表示一個數字，那麼就可以用另一個變數I來表示：

Iy≈32L(B−b)−12IxI_y \approx \frac{3}{2}L(B-b) - \frac{1}{2}I_xIy​≈23​L(B−b)−21​Ix​

其實程式碼中下面 下麪這條語句就是套用的這個公式。

程式碼中利用了一個右移運算表示公式中的12\frac{1}{2}21​，而32L(B−b)\frac{3}{2}L(B-b)23​L(B−b)就是求出程式碼中這串神祕數位的基礎，至於怎麼求得的，只有作者知道。後面又有一位大佬對這串數位進行推導，經過精密的演算求得了一串新的數位0x5f375a86，它略優於原常數，大佬只管算，我們膜拜就好。

因爲上文中含I的公式是從整型的角度計算的，所以需要強制型別轉換將整形轉回浮點型，緊接着最後一行程式碼是利用牛頓迭代法提高結果的精確度，沒有什麼驚奇之處，下面 下麪回顧一下上文過程中作者的幾個騷操作：

• 用整數型表示浮點型
• log2(1+mx)≈mx+blog_2(1+m_x)\approx m_x+blog2​(1+mx​)≈mx​+b約等關係的替換
• LE+MLE+MLE+M捆綁二進制

也許作者利用的想法是已經存在了很久的理論，但是能把這些理論相組合並靈活運用創造出這種新興高效的演算法，真的不得不感嘆一句NiuB，但需要注意的是這個演算法依賴於浮點數的儲存和位元組順序，所以在Mac上行不通。

上面程式碼可以再精簡一些，但是原理一致，只是將一些變數簡化：

float InSqrt(float x)
{
	float xhalf = 0.5f * x;  #公衆號【測試員小何
	int i = *(int*)&x;
	i = 0x5f3759df - (i>>i);
	x = *(float*)&i;
	x = x*(1.5f-xhalf*x*x);
	return x; 
}

可能你看到最後還是那句"what the fuck"，畢竟太多的公式推導都並沒有相應的理論依據，只是靠着作者這些腦洞大開的想法，難道就是「我不要你覺得，我只要我覺得?」，關鍵還是要瞭解一下流程中幾處很牛逼的想法，平時程式設計中不失爲一種辦法嘛，也可以當成一次知識拓展。

如果對軟體測試有興趣，想瞭解更多的測試知識，解決測試問題,以及入門指導，
幫你解決測試中遇到的困惑，我們這裏有技術高手。如果你正在找工作或者剛剛學校出來，
又或者已經工作但是經常覺得難點很多，覺得自己測試方面學的不夠精想要繼續學習的，
想轉行怕學不會的，都可以加入我們644956177。
羣內可領取最新軟體測試大廠面試資料和Python自動化、介面、框架搭建學習資料！