字串匹配的KMP演算法

字串匹配是計算機的基本任務之一。

演算法複雜度O(m+n)

舉例來說，有一個字串"BBC ABCDAB ABCDABCDABDE"，我想知道，裏面是否包含另一個字串"ABCDABD"？

許多演算法可以完成這個任務，Knuth-Morris-Pratt演算法（簡稱KMP）是最常用的之一。它以三個發明者命名，起頭的那個K就是著名科學家Donald Knuth。

這種演算法不太容易理解，網上有很多解釋，但讀起來都很費勁。直到讀到Jake Boxer的文章，我才真正理解這種演算法。下面 下麪，我用自己的語言，試圖寫一篇比較好懂的KMP演算法解釋。

首先，字串"BBC ABCDAB ABCDABCDABDE"的第一個字元與搜尋詞"ABCDABD"的第一個字元，進行比較。因爲B與A不匹配，所以搜尋詞後移一位。

因爲B與A不匹配，搜尋詞再往後移。

就這樣，直到字串有一個字元，與搜尋詞的第一個字元相同爲止。

接着比較字串和搜尋詞的下一個字元，還是相同。

直到字串有一個字元，與搜尋詞對應的字元不相同爲止。

這時，最自然的反應是，將搜尋詞整個後移一位，再從頭逐個比較。這樣做雖然可行，但是效率很差，因爲你要把"搜尋位置"移到已經比較過的位置，重比一遍。

一個基本事實是，當空格與D不匹配時，你其實知道前面六個字元是"ABCDAB"。KMP演算法的想法是，設法利用這個已知資訊，不要把"搜尋位置"移回已經比較過的位置，繼續把它向後移，這樣就提高了效率。

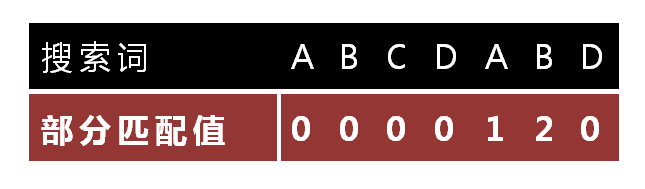
怎麼做到這一點呢？可以針對搜尋詞，算出一張《部分匹配表》（Partial Match Table）。這張表是如何產生的，後面再介紹，這裏只要會用就可以了。

已知空格與D不匹配時，前面六個字元"ABCDAB"是匹配的。查表可知，最後一個匹配字元B對應的"部分匹配值"爲2，因此按照下面 下麪的公式算出向後移動的位數：

移動位數 = 已匹配的字元數 - 對應的部分匹配值

因爲 6 - 2 等於4，所以將搜尋詞向後移動4位元。

因爲空格與Ｃ不匹配，搜尋詞還要繼續往後移。這時，已匹配的字元數爲2（「AB」），對應的"部分匹配值"爲0。所以，移動位數 = 2 - 0，結果爲 2，於是將搜尋詞向後移2位。

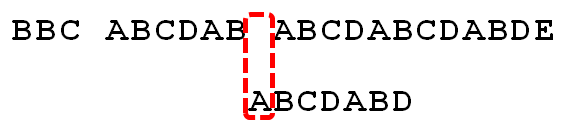
因爲空格與A不匹配，繼續後移一位。

逐位比較，直到發現C與D不匹配。於是，移動位數 = 6 - 2，繼續將搜尋詞向後移動4位元。

逐位比較，直到搜尋詞的最後一位，發現完全匹配，於是搜尋完成。如果還要繼續搜尋（即找出全部匹配），移動位數 = 7 - 0，再將搜尋詞向後移動7位，這裏就不再重複了。

下面 下麪介紹《部分匹配表》是如何產生的。

首先，要瞭解兩個概念：「字首"和"後綴」。 "字首"指除了最後一個字元以外，一個字串的全部頭部組合；"後綴"指除了第一個字元以外，一個字串的全部尾部組合。

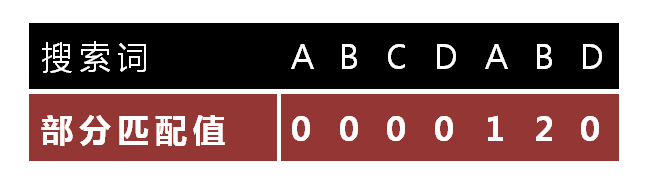
"部分匹配值"就是"字首"和"後綴"的最長的共有元素的長度。以"ABCDABD"爲例，

－　"A"的字首和後綴都爲空集，共有元素的長度爲0；

－　"AB"的字首爲[A]，後綴爲[B]，共有元素的長度爲0；

－　"ABC"的字首爲[A, AB]，後綴爲[BC, C]，共有元素的長度0；

－　"ABCD"的字首爲[A, AB, ABC]，後綴爲[BCD, CD, D]，共有元素的長度爲0；

－　「ABCDA"的字首爲[A, AB, ABC, ABCD]，後綴爲[BCDA, CDA, DA, A]，共有元素爲"A」，長度爲1；

－　「ABCDAB"的字首爲[A, AB, ABC, ABCD, ABCDA]，後綴爲[BCDAB, CDAB, DAB, AB, B]，共有元素爲"AB」，長度爲2；

－　"ABCDABD"的字首爲[A, AB, ABC, ABCD, ABCDA, ABCDAB]，後綴爲[BCDABD, CDABD, DABD, ABD, BD, D]，共有元素的長度爲0。

"部分匹配"的實質是，有時候，字串頭部和尾部會有重複。比如，「ABCDAB"之中有兩個"AB」，那麼它的"部分匹配值"就是2（"AB"的長度）。搜尋詞移動的時候，第一個"AB"向後移動4位元（字串長度-部分匹配值），就可以來到第二個"AB"的位置。