Python計算機視覺程式設計第六章 影象聚類
本章將介紹幾種聚類方法,並展示如何利用他們對影象進行聚類,從而尋找相似的影象組。聚類可以用於識別、劃分影象數據集,組織和導航。此外,我們還會對聚類後的影象進行相似性視覺化。
1 K-means聚類
K-means是一種將輸入數據劃分成k個簇的簡單聚類演算法。K-means反覆 反復提煉初始評估的類中心,步驟如下:
1)以隨機或猜測的方式初始化類中心,i=1…k;
2)將每個數據點歸併到離他距離最近的類中心所屬的類;
3)對所有屬於該類的數據點球平均,將平均值作爲新的類中心;
4)重複步驟2)和步驟3)直到收斂。
K-means試圖使類內總方差最小:xj是輸入數據,並且是向量。該演算法是啓發式提煉演算法,在很多情況下都適用,但是並不能保證得到最優的結果。爲了避免初始化類中心是沒選取好類中心初值所造成的的影響,該演算法通常會初始化不同的類中心進行多次運算,然後選擇方差V最小的結果。
K-means演算法最大的缺陷是必須餘弦設定聚類數k,如果選擇不恰當則會導致聚類出來的結果很差。其優點是很容易實現,可以並行計算,並且對於很多別的問題不需要任何調整就能夠直接使用。
1.1 Scipy聚類包
儘管K-means演算法很容易實現,但我們沒有必要自己實現它,Scipy向量量化包scipy.cluster.vq中有K-means的實現,下面 下麪是使用方法:
from pylab import *
from scipy.cluster.vq import *
# 生成簡單的二維數據
class1 = 1.5 * randn(100,2)
class2 = randn(100,2) + array([5,5])
features = vstack((class1, class2))
# 用k=2對這些數據進行聚類
centroids, variance = kmeans(features, 2)
# 由於Scipy中實現的K-means會預設計算20次,併爲我們選擇方法最下的結果,所有這裏返回的方差並不是我們所需要的。
# 現在,可以用Scipy包中的向量量化函數對每個數據點進行歸類
code, distance = vq(features, centroids)
# 通過上面得到的code,我們可以檢查是否有歸類錯誤。
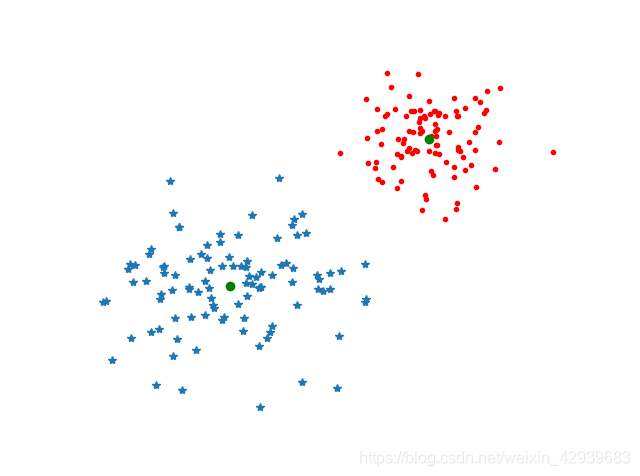
# 爲了將其視覺化,我們可以畫出這些數據點及最終的聚類中心
figure()
ndx = where(code==0)[0]
plot(features[ndx,0],features[ndx,1],'*')
ndx = where(code==1)[0]
plot(features[ndx,0],features[ndx,1],'r.')
plot(centroids[:,0],centroids[:,1],'go')
axis('off')
show()
1.2 影象聚類
我們用K-means對字型影象進行聚類。檔案selectedfontimage.zip包含66幅來自該字型數據集fontimages的影象,用pickle模組載入模型檔案,在主成分上對影象進行投影,然後用下面 下麪的方法聚類:
from PCV.tools import imtools
import pickle
from scipy import *
from pylab import *
from PIL import Image
from scipy.cluster.vq import *
from PCV.tools import pca
# 獲取selected-fontimages 檔案下影象檔名,並儲存在列表中
imlist = imtools.get_imlist('D:\\123\影象處理\Image Processing\Image Processing\Chapter6\selectedfontimages\\a_selected_thumbs')
imnbr = len(imlist)
# 獲取影象列表和他們的尺寸
im = array(Image.open(imlist[0]))
m, n = im.shape[:2]
imnbr = len(imlist)
# 建立矩陣,儲存所有拉成一組形式後的影象
immatrix = array([array(Image.open(im)).flatten() for im in imlist],'f')
# PCA降維
V, S, immean = pca.pca(immatrix)
# 儲存均值和主成分
# f = open('D:\\123\影象處理\Image Processing\Image Processing\Chapter6\\font_pca_modes.pkl','wb')
# pickle.dump(immean, f)
# pickle.dump(V, f)
# f.close()
# 載入模型檔案
with open('D:\\123\影象處理\Image Processing\Image Processing\Chapter6\\font_pca_modes.pkl','rb') as f:
immean = pickle.load(f)
V = pickle.load(f)
# 投影到前40個主成分上
immean = immean.flatten()
projected = array([dot(V[:40], immatrix[i] - immean) for i in range(imnbr)])
# 進行k-means聚類
projected = whiten(projected)
centroids, distortion = kmeans(projected,4)
code, distance = vq(projected, centroids)
# 繪製聚類簇
for k in range(4):
ind = where(code==k)[0]
figure()
gray()
for i in range(minimum(len(ind), 40)):
subplot(4,10,i+1)
imshow(immatrix[ind[i]].reshape((25,25)))
axis('off')
show()

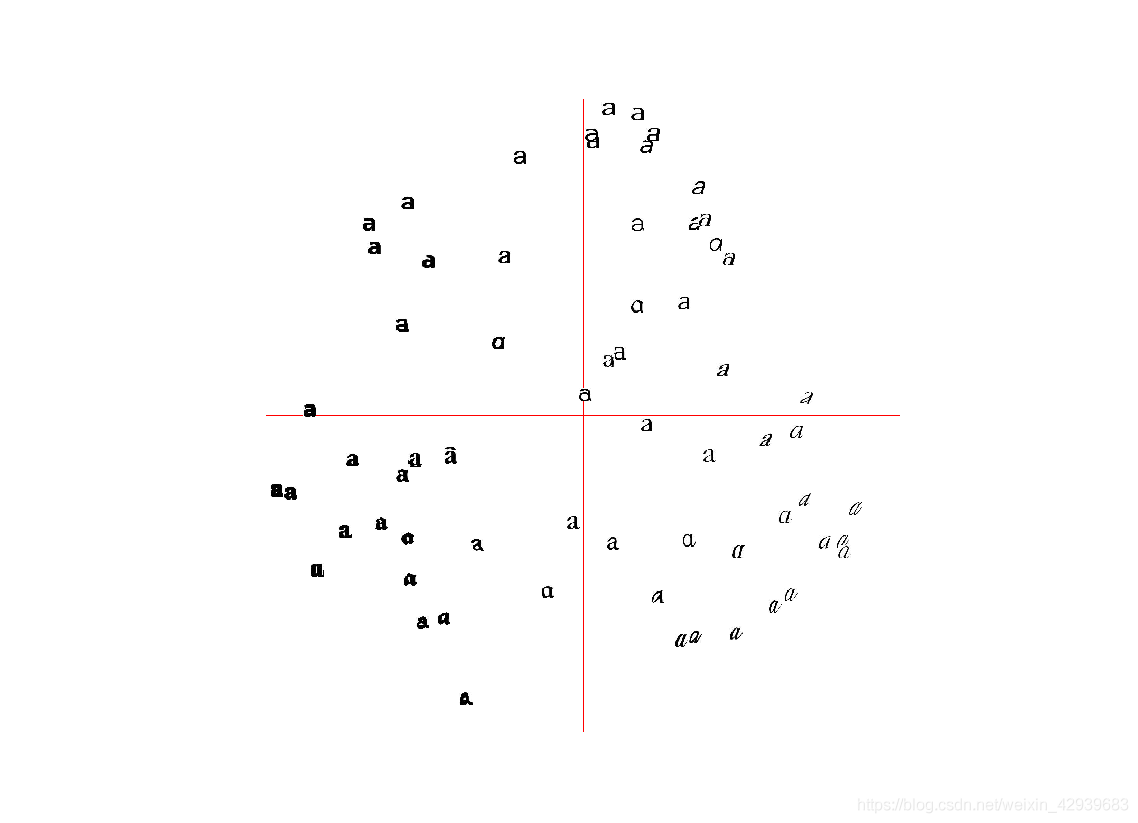
1.3 在主成分上視覺化影象
爲了便於觀察上面是如何利用主成分進行聚類的,我們可以在一對主成分方向的座標上視覺化這些影象。一種方法是將影象投影到兩個主成分上,改變投影爲:
projected = array([dot(V[[0,2]],immatrix[i]-immean) for i in range(imnbr)]
以得到相應的座標(在這裏V[[0,2]]分別是第一個和第三個主成分)。當然,你也可以將其投影到所有成分上,之後挑選出你需要的列:
from PCV.tools import imtools, pca
from PIL import Image, ImageDraw
from pylab import *
from PCV.clustering import hcluster
imlist = imtools.get_imlist('D:\\123\影象處理\Image Processing\Image Processing\Chapter6\selectedfontimages\\a_selected_thumbs')
imnbr = len(imlist)
# Load images, run PCA.
immatrix = array([array(Image.open(im)).flatten() for im in imlist], 'f')
V, S, immean = pca.pca(immatrix)
# Project on 2 PCs.
projected = array([dot(V[[0, 1]], immatrix[i] - immean) for i in range(imnbr)])
# 高和寬
h, w = 1200, 1200
# 建立一幅白色背景圖
img = Image.new('RGB', (w, h), (255, 255, 255))
draw = ImageDraw.Draw(img)
# 繪製座標軸
draw.line((0, h / 2, w, h / 2), fill=(255, 0, 0))
draw.line((w / 2, 0, w / 2, h), fill=(255, 0, 0))
# 縮放以適應座標系
scale = abs(projected).max(0)
scaled = floor(array([(p / scale) * (w / 2 - 20, h / 2 - 20) + (w / 2, h / 2)
for p in projected])).astype(int)
# 貼上每幅影象的縮圖到白色背景圖片
for i in range(imnbr):
nodeim = Image.open(imlist[i])
nodeim.thumbnail((25, 25))
ns = nodeim.size
box = (scaled[i][0] - ns[0] // 2, scaled[i][1] - ns[1] // 2,
scaled[i][0] + ns[0] // 2 + 1, scaled[i][1] + ns[1] // 2 + 1)
img.paste(nodeim, box)
tree = hcluster.hcluster(projected)
hcluster.draw_dendrogram(tree, imlist, filename='fonts.png')
figure()
imshow(img)
axis('off')
img.save('D:\\123\影象處理\Image Processing\Image Processing\Chapter6\\pca_font.png')
show()
1.4 畫素聚類
在結束本節之前,我們來看一個對單幅影象中的畫素而非全部影象進行聚類的例子。將影象區域或畫素合併成有意義的部分稱爲影象分割。單純在畫素水平上應用 K-means可以用於一些簡單影象的影象分割,但是對於複雜影象得出的結果往往是毫無意義的。要產生有意義的結果,往往需要更復雜的類模型而非平均畫素色彩或空間一致性。
from scipy.cluster.vq import *
from scipy import *
from pylab import *
from PIL import Image
steps = 50 # 影象被劃分成steps×steps的區域
im = array(Image.open('D:\\123\影象處理\Image Processing\Image Processing\Chapter6\empire.jpg'))
dx = im.shape[0] // steps
dy = im.shape[1] // steps
# 計算每個區域的顏色特徵
features = []
for x in range(steps):
for y in range(steps):
R = mean(im[x*dx:(x+1)*dx, y*dy:(y+1)*dy,0])
G = mean(im[x*dx:(x+1)*dx, y*dy:(y+1)*dy,1])
B = mean(im[x*dx:(x+1)*dx, y*dy:(y+1)*dy,2])
features.append([R,G,B])
features = array(features,'f')
# 聚類
centroids, variance = kmeans(features, 3)
code, distance = vq(features, centroids)
# 用聚類標記建立影象
codeim = code.reshape(steps, steps)
#codeim = imresize(codeim, im.shape[:2], 'nearest')
figure()
ax1 = subplot(121)
title('Original Image')
axis('off')
imshow(im)
ax2 = subplot(122)
title('After Clustering')
axis('off')
imshow(codeim)
show()
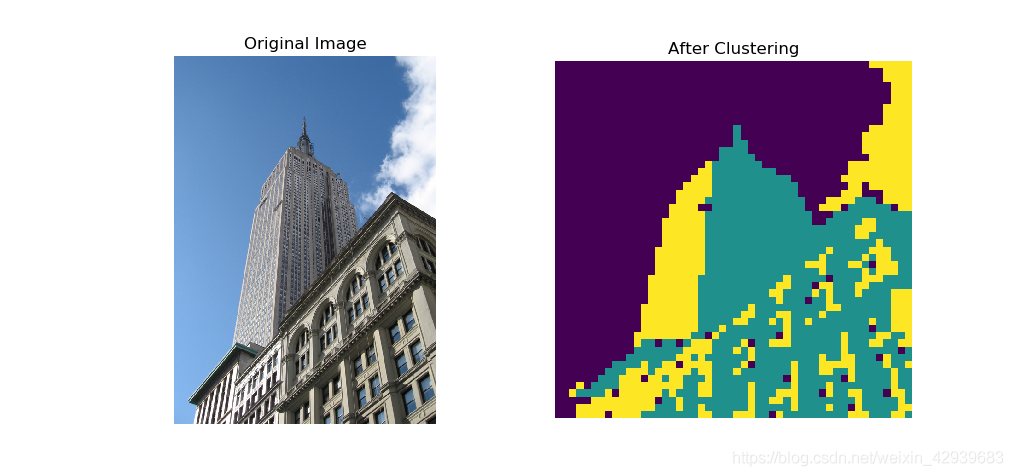
從結果可以看出畫素聚類還是具有一定的可行性的,演算法將影象分爲了天空,樓房的向陽面和向陰面。儘管利用視窗對影象進行了下採樣,但結果仍然是由噪聲的。如果影象某些區域沒有空間一致性,則很難將其分開,如圖中向陽面中的屋檐處。空間一致性和更好的分割方法以及其他的影象分割演算法會在後面討論,現在,讓我們繼續來看下一個基本的聚類演算法。
2 層次聚類
層次聚類(或凝聚式聚類)是另一種簡單但有效的聚類演算法,其思想是基於樣本間成對距離建立一個簡相似性樹。該演算法首先將特徵向量距離最近的兩個樣本歸併爲一組,並在樹中建立一個「平均節點」,將這兩個距離最近的樣本作爲該「平均」節點下的子節點;然後在剩下的包含任意平均節點的樣本中尋找下一個最近的對,重複進行前面的操作。在每一個節點處儲存了兩個子節點之間的距離。遍歷整個樹,通過設定的閾值,遍歷過程可以在比閾值大的節點位置終止,從而提取出聚類簇。
層次聚類由若幹優點,例如,利用樹結構可以視覺化數據間的關係,並顯示這些簇是如何關聯的。在樹中,一個好的特徵向量可以給出一個很好的分離結果。另外一個優點是,對於給定的不同的閾值,可以直接利用原來的樹,而不需要重新計算。不足之處是,對於實際需要的聚類簇,我們需要選擇一個合適的閾值。
建立檔案hcluster.py,將下面 下麪程式碼新增進去:
from itertools import combinations
from pylab import *
class ClusterNode(object):
def __init__(self,vec,left,right,distance=0.0,count=1):
self.left = left
self.right = right
self.vec = vec
self.distance = distance
self.count = count
def extract_clusters(self, dist):
"""從層次聚類樹中提取距離小於dist的子樹簇羣列表"""
if self.distance < dist:
return [self]
return self.left.extract_clusters(dist) + self.right.extract_clusters(dist)
def get_cluster_elements(self):
"""在聚類子樹中返回元素的id"""
return self.left.get_cluster_elements() + self.right.get_cluster_elements()
def get_height(self):
"""返回節點的高度,高度是各分支的和"""
return self.left.get_height() + self.right.get_height()
def get_depth(self):
"""返回節點的深度,深度是每個子節點取最大再加上它的自身距離"""
return max(self.left.get_depth(), self.right.get_depth()) + self.distance
class ClusterLeafNode(object):
def __init__(self,vec,id):
self.vec = vec
self.id = id
def extract_clusters(self, dist):
return [self]
def get_cluster_elements(self):
return [self.id]
def get_height(self):
return 1
def get_depth(self):
return 0
def L2dist(v1,v2):
return sqrt(sum((v1-v2)**2))
def L1dist(v1,v2):
return sum(abs(v1-v2))
def hcluster(features,distfcn=L2dist):
"""用層次聚類對行特徵進行聚類"""
# 用於儲存計算出的距離
distances = {}
# 每行初始化爲一個簇
node = [(ClusterLeafNode(array(f), id=i) for i, f in enumerate(features))]
while len(node) > 1:
closet = float('Inf')
# 遍歷每對,尋找最小距離
for ni, nj in combinations(node, 2):
if (ni, nj) not in distances:
distances[ni, nj] = distfcn(ni.vec, nj.vec)
d = distances[ni, nj]
if d < closet:
closet = d
lowestpair = (ni, nj)
ni, nj = lowestpair
# 對兩個簇求平均
new_vec = (ni.vec + nj.vec) / 2.0
# 建立新的節點
new_node = ClusterNode(new_vec, left=ni, right=nj, distance=closet)
node.remove(ni)
node.remove(nj)
node.append(new_node)
return node[0]
我們爲樹節點建立了兩個類,即ClusterNode和ClusterLeafNode,這兩個類將用於建立聚類樹,其中函數hcluster()用於建立樹。首先建立一個包含葉節點的列表,然後根據選擇的距離度量方式將距離最近的對歸併到一起,返回的終節點即爲樹的根。對於一個行爲特徵向量的矩陣,執行hcluster()會建立和返回聚類樹。
距離度量的選擇依賴於實際的特徵向量,利用歐式距離L2(同時提供了L1距離度量函數),可以建立任意距離度量函數,並將它作爲參數傳遞給hcluster()。對於每個子樹,計算其所有節點特徵向量的平均值,作爲新的特徵向量來表示該子樹,並將每個子樹視爲一個物件。當然,還有其他將哪兩個節點合併在一起的方案,比如在兩個子樹中使用物件間距離最小的單向鎖,及在兩個子樹中用物件間距離最大的完全鎖。選擇不同的鎖會生成不同類型的聚類樹。
下面 下麪,我們在一個簡單例子中觀察該聚類過程:
class1 = 1.5 * randn(100, 2)
class2 = randn(100, 2) + array([5, 5])
features = vstack((class1, class2))
tree = hcluster.hcluster(features)
clusters = tree.extract_clusters(5)
print('number of clusters', len(clusters))
for c in clusters:
print(c.get_cluster_elements())

全連線的凝聚層次聚類的操作步驟:
1、獲取所有樣本的距離矩陣
2、將每個數據點作爲一個單獨的簇
3、基於最不相似(距離最遠)樣本的距離,合併兩個最接近的簇
4、更新樣本的距離矩陣
5、重複2到4,直到所有樣本都屬於同一個簇爲止。
下面 下麪編寫程式碼實現上面的操作:
1、獲取樣本
隨機產生5個樣本,每個樣本包含3個特徵(x,y,z)
import pandas as pd
import numpy as np
np.random.seed(1)
# 設定特徵名稱
variable = ["x","y","z"]
# 設定標號
labels = ["s1","s2","s3","s4","s5"]
# 產生一個(5,3)的陣列
data = np.random.random_sample([5,3])*10
# 通過pandas將陣列轉化成一個DataFrame
df = pd.DataFrame(data,columns=variable,index=labels)
# 檢視數據
print(df)
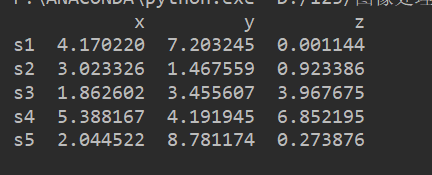
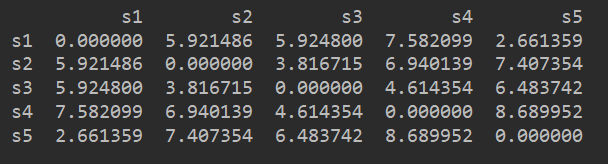
2、獲取所有樣本的距離矩陣
通過SciPy來計算距離矩陣,計算每個樣本間兩兩的歐式距離,將矩陣矩陣用一個DataFrame進行儲存,方便檢視:
from scipy.spatial.distance import pdist,squareform
# 獲得距離矩陣
"""
pdist:計算兩兩樣本間的歐式距離,返回的是一個一維陣列
squareform:將陣列轉換成一個對稱矩陣
"""
dist_matrix = pd.DataFrame(squareform(pdist(df,metric="euclidean")),
columns=labels,index=labels)
print(dist_matrix)
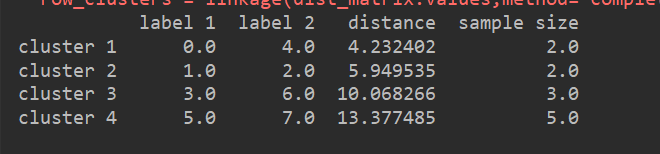
3、獲取全連線矩陣的關聯矩陣
通過scipy的linkage函數,獲取一個以全連線作爲距離判定標準的關聯矩陣(linkage matrix)
from scipy.cluster.hierarchy import linkage
# 以全連線作爲距離判斷標準,獲取一個關聯矩陣
row_clusters = linkage(dist_matrix.values,method="complete",metric="euclidean")
#將關聯矩陣轉換成爲一個DataFrame
clusters = pd.DataFrame(row_clusters,columns=["label 1","label 2","distance","sample size"],
index=["cluster %d"%(i+1) for i in range(row_clusters.shape[0])])
print(clusters)
4、通過關聯矩陣繪製樹狀圖
使用scipy的dendrogram來繪製樹狀圖
from scipy.cluster.hierarchy import dendrogram
import matplotlib.pyplot as plt
row_dendr = dendrogram(row_clusters,labels=labels)
plt.tight_layout()
plt.ylabel("歐式距離")
plt.show()
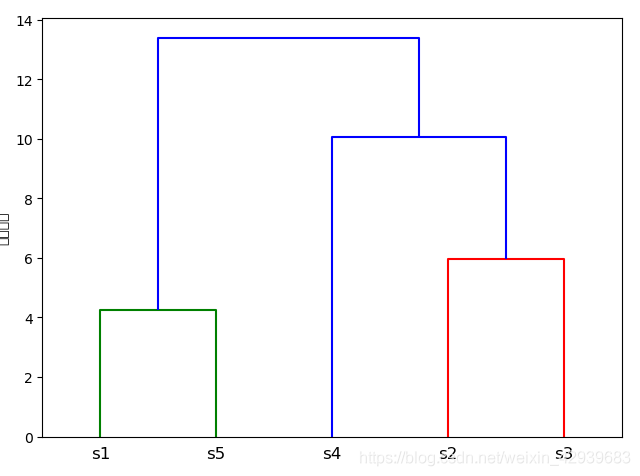
通過上面的樹狀圖,可以直觀的發現。首先是s1和s5合併,s2和s3合併,然後s2、s3、s4合併,最後再和s1、s5合併。
我們下面 下麪來看一個基於影象顏色資訊對影象進行聚類的例子。檔案sunsets.zip中包含100張影象。在這個例子中,我們用顏色直方圖作爲每幅影象的特徵向量。雖然這樣處理有些簡單粗糙,但仍然能夠很好地說明分層聚類地過程。在包含這些日落影象的資料夾中執行下面 下麪的程式碼:
import os
from PCV.clustering import hcluster
from matplotlib.pyplot import *
from numpy import *
from PIL import Image
# 建立影象列表
path = 'D:\\123\影象處理\Image Processing\Image Processing\Chapter6\\flickr-sunsets-small\\'
imlist = [os.path.join(path,f) for f in os.listdir(path) if f.endswith('.jpg')]
# 提取特徵向量,每個顏色通道量化成8個小區間
features = zeros([len(imlist), 512])
for i,f in enumerate(imlist):
im = array(Image.open(f))
# 多維直方圖
h, edges = histogramdd(im.reshape(-1, 3), 8, normed=True, range=[(0, 255), (0, 255), (0, 255)])
features[i] = h.flatten()
tree = hcluster.hcluster(features)
# 設定一些(任意的)閾值以視覺化聚類簇
clusters = tree.extract_clusters(0.23 * tree.distance)
# 繪製聚類簇中元素超過 3 個的那些影象
for c in clusters:
elements = c.get_cluster_elements()
nbr_elements = len(elements)
if nbr_elements > 3:
figure()
for p in range(minimum(nbr_elements, 20)):
subplot(4, 5, p + 1)
im = array(Image.open(imlist[elements[p]]))
imshow(im)
axis('off')
show()
hcluster.draw_dendrogram(tree, imlist, filename='sunset.jpg')



3 譜聚類
譜聚類方法是一種有趣的聚類演算法,與前面的K-means和層次聚類方法截然不同。
對於n個元素(如n幅影象),相似矩陣(或親和矩陣,有時也稱爲距離矩陣)是一個n×n的矩陣,矩陣每個元素表示兩兩之間的相似性分數。譜聚類是由相似性矩陣構建譜矩陣而得名的。對該譜矩陣進行特徵分解得到的特徵向量可以用於降維,然後聚類。
譜聚類的優點之一是僅需輸入相似性矩陣,並且可以採用你所想到的任意度量方式構建該相似性矩陣。像K-means和層次聚類需要計算那些特徵向量求平均;爲了計算平均值,會將特徵或描述子限製爲向量。而對於譜方法,特徵向量就沒有類別限制,只要有一個「距離」或「相似性」的概念即可。
下面 下麪說明譜聚類的過程。給定一個n×n的相似矩陣S,sij爲相似性分數,我們可以建立一個矩陣,稱爲拉普拉斯矩陣:其中,I是單位矩陣,D是對角矩陣,對角線上的元素是S對應行元素之和,D=diag(di),di=sij。拉普拉斯矩陣的D-1/2爲:爲了簡潔表示,使用較小的值並且要求sij⩾0。
計算L的特徵向量,並使用k個最大特徵值對應的k個特徵向量,構建出一個特徵向量集,從而可以找到聚類簇。建立一個矩陣,該矩陣的各列是由之前求出的k個特徵向量構成,每一行可以看作一個新的特徵向量,長度爲k。本質上,譜聚類演算法是將原始空間中的數據轉換成更容易聚類的新特徵向量。在某些情況下,不會首先使用聚類演算法。
我們來看看真實的例子中譜聚類演算法的程式碼,使用K-means例子中的字型影象:
from PCV.tools import imtools, pca
from PIL import Image, ImageDraw
from pylab import *
from scipy.cluster.vq import *
# 獲取selected-fontimages 檔案下影象檔名,並儲存在列表中
imlist = imtools.get_imlist('D:\\123\影象處理\Image Processing\Image Processing\Chapter6\selectedfontimages\\a_selected_thumbs')
imnbr = len(imlist)
# 建立矩陣,儲存所有拉成一組形式後的影象
immatrix = array([array(Image.open(im)).flatten() for im in imlist],'f')
# PCA降維
V, S, immean = pca.pca(immatrix)
# 投影到前兩個主成分上
projected = array([dot(V[[0, 1]], immatrix[i] - immean) for i in range(imnbr)])
n = len(projected)
# 計算距離矩陣
S = array([[ sqrt(sum((projected[i]-projected[j]) **2 )) for i in range(n) ] for j in range(n)], 'f')
# 建立拉普拉斯矩陣
rowsum = sum(S, axis=1)
D = diag(1 / sqrt(rowsum))
I = identity(n)
L = I - dot(D,dot(S,D))
# 計算矩陣L的特徵向量
U, sigma, V = linalg.svd(L)
k = 5
# 從矩陣L的前k個特徵向量(eigenvector)中建立特徵向量(feature vector)
# 疊加特徵向量作爲陣列的列
features = array(V[:k]).T
# k-means 聚類
features = whiten(features)
centroids, distortion = kmeans(features, k)
code, distance = vq(features, centroids)
# 繪製聚類簇
for c in range(k):
ind = where(code == c)[0]
figure()
gray()
for i in range(minimum(len(ind), 39)):
im = Image.open(imlist[ind[i]])
subplot(4, 10, i + 1)
imshow(array(im))
axis('equal')
axis('off')
show()
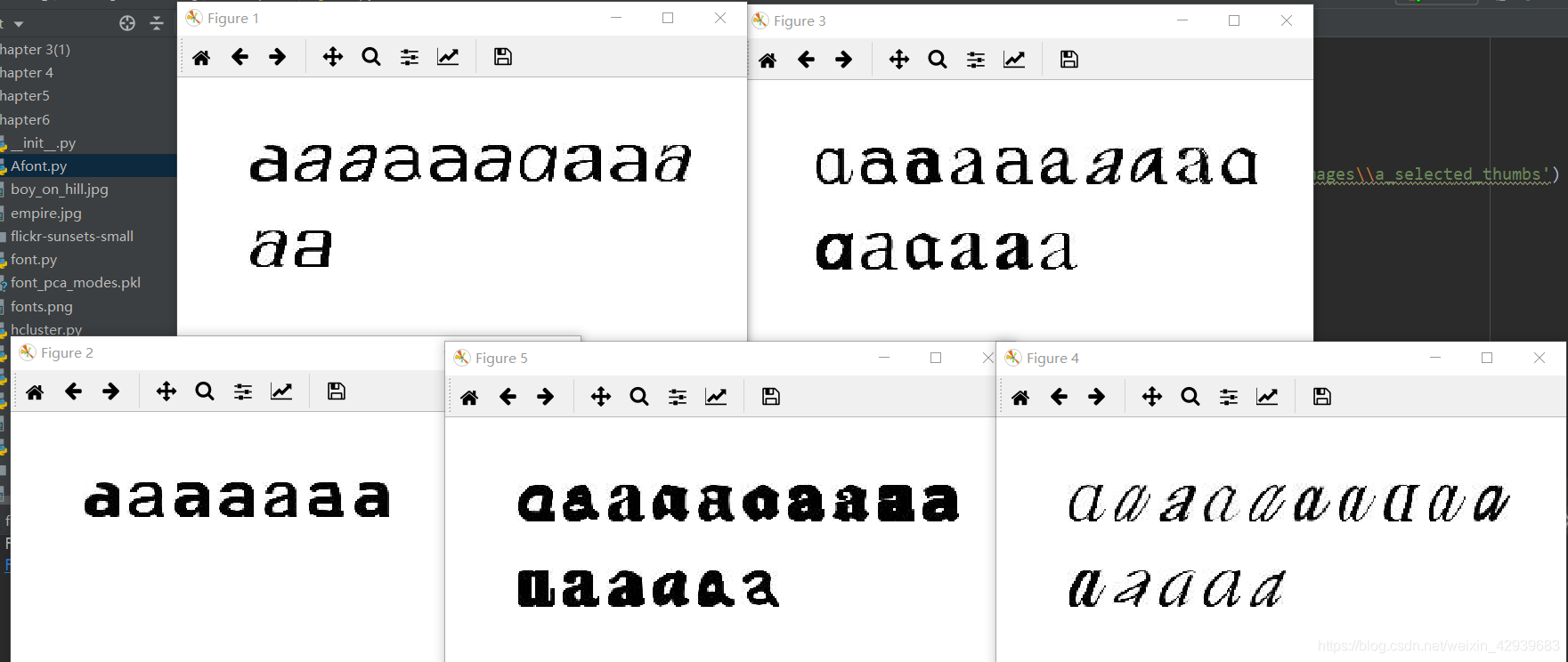
實驗中,用兩兩間的歐式距離建立矩陣S,並對k個特徵向量用常規的K-means進行聚類。注意,矩陣V包含的是對特徵值進行排序後的特徵向量。然後,繪製出這些聚類簇。觀察到,上面分別顯示出了五類,根據不同的特徵向量,將相同的類聚集起來,形成這些聚類影象。