初步學習k-NN演算法以及使用GridSearchCV進行調參

k最近鄰演算法 (k-NN)

  k最近鄰 (k-Nearst Neighbor, k-NN) 演算法是一種比較簡單易懂的機器學習演算法，1968年由Cover和Hart提出，常應用於字元識別、文字分類、影象識別等領域。該演算法的思想是：一個樣本與數據集中的k個樣本最相似，如果這k個樣本中的大多數屬於某一個類別，則該樣本也屬於這個類別。
  在sklearn庫中，k-NN包含在sklearn.neighbors中，有k最近鄰分類KNeighborsClassifier和k最近鄰迴歸KNeighborsRegressor。本文以k-NN分類器爲例進行學習。
  sklearn庫中的k-NN方法有很多超參數，常用的超參數如下：
  1. weights：用於分配權重。基本的最近鄰迴歸使用統一的權重，即本地鄰域內的每個鄰點對查詢點的分類貢獻一致。在某些環境下，對鄰點加權可能是有利的，使得附近點對於迴歸所作出的貢獻多於遠處點。預設爲weights = 'uniform'，表示爲所有點分配同等權重。weights = 'distance'表示分配的權重與查詢點距離呈反比。此外，我們還可以自定義一個距離函數用來計算權重。
  2. n_neighbors：鄰居個數。
  3. p：p參數只有在weights = 'distance'時纔有。p是一個大於或等於1的值。p = 1表示曼哈頓距離 (Manhattan Distance)，p = 2表示歐式距離 (Euclidean Distance)，p = ∞表示它是各個座標距離的最大值。
  下面 下麪介紹一下三種距離計算公式。設特徵空間$\mathcal{X}$是$n$維實數向量空間$R_{n}$，$x_{i},x_{j}\in\mathcal{X}$，$x_{i}=(x_{i}^{(1)},x_{i}^{(2)},...,x_{i}^{(n)})^{T}$，$x_{j}=(x_{j}^{(1)},x_{j}^{(2)},...,x_{j}^{(n)})^{T}$，$x_{i},x_{j}$的$L_{p}$距離定義爲$L_p(x_i,x_j) = (\sum_{l=1}^{n} \; |x_i^{(l)}-x_j^{(l)}|^p)^{\frac{1}{p}}.$上式中$p\geq1$. 當$p=1$時，稱爲曼哈頓距離，此時$L_1(x_i,x_j)= \sum_{l=1}^{n} |x_i^{(l)}-x_j^{(l)}|.$當$p=2$時，稱爲歐式距離，此時$L_2(x_i,x_j) = (\sum_{l=1}^{n} \; |x_i^{(l)}-x_j^{(l)}|^{2})^{\frac{1}{2}}.$當$p=\infty$時，表示各個座標距離的最大值，此時$L_{\infty}(x_i,x_j)= \mathop{max}_l \; |x_i^{(l)}-x_j^{(l)}|.$
  接下來簡單說明一下k-NN的演算法流程。輸入訓練數據集$T=(x_{1},y_{1}),(x_{2},y_{2}),...,(x_{N},y_{N}),$其中$x_{i}\in\mathcal{X}\subseteq R^{n}$爲範例的特徵向量，$y_{i}\in\mathcal{Y}=\{c_1,c_2,...,c_k\}$爲範例的類別，$i=1,2,...,N$；範例特徵向量$x$.
  1. 根據給點的距離度量，在訓練集$T$中找出與$x$最近鄰的$k$個點，涵蓋着$k$個點的領域，記爲$N_k(x)$.
  2. 在$N_k(x)$中根據分類決策規則（如多數表決），決定$x$的類別$y$：$y=arg \mathop{\; max}_{c_j} {\sum}_{x_i \in N_k(x)} \; I(y_i=c_j) , i=1,2,...,N;$在上式中，$I$爲指示函數，即當$y_i=c_j$時，$I$爲$1$，否則$I$爲$0$.
  最後輸出範例$x$所屬的類$y$.
  k-NN的特殊情況是k=1的情形，稱爲最近鄰演算法。對於輸入的範例點（特徵向量）$x$，最近鄰演算法將訓練數據集中與$x$最近鄰點的類作爲$x$的類。

GridSearchCV調參

  GridSearchCV包含在sklearn.model_selection中。它可以拆分爲「GridSearch」和「CV」兩個部分，即網格搜尋和交叉驗證。網格搜尋用於選取模型的最優超參數。獲取最優超參數的方式可以繪製驗證曲線，但是驗證曲線只能每次獲取一個最優超參數。如果多個超參數有很多排列組合的話，就可以使用網格搜尋尋求最優超參數的組合。網格搜尋針對超參數組合列表中的每一個組合，範例化給定的模型，進行交叉驗證，將平均得分最高的超參數組合作爲最佳的選擇，返回模型物件。

GridSearchCV(estimator, param_grid, scoring=None, fit_params=None, n_jobs=1, iid=True,
             refit=True, cv=None, verbose=0, pre_dispatch='2*n_jobs', error_score='raise',
             return_train_score=True)

  以下是GridSearchCV方法中常用的超參數。
  1. estimator：建立的演算法物件。
  2. param_grid：值爲字典或者列表，需要最佳化的參數的取值。
  3. scoring：準確度評價標準，預設None,這時需要使用score函數；或者如scoring='roc_auc'，根據所選模型不同，評價準則不同。字串（函數名）或是可呼叫物件，需要其函數簽名，形如scorer(estimator, X, y)；如果是None，則使用estimator的誤差估計函數。
  4. n_jobs：並行數，預設爲1，n_jobs = -1表示跟CPU核數一致。
  5. cv：交叉驗證參數，預設None，使用三折交叉驗證。指定fold數量，預設爲3，也可以是yield訓練或測試數據的生成器。
  6. verbose：日誌冗長度。verbose = 0表示不輸出訓練過程，verbose = 1表示偶爾輸出，verbose > 1表示對每個子模型都輸出。
  GridSearchCV還內建了一些屬性。
  1. best_estimator_：效果最好的分類器。
  2. best_score_：成員提供優化過程期間觀察到的最好的評分。
  3. best_params_：描述了已取得最佳結果的參數的組合。
  4. best_index_：對應於最佳候選參數設定的索引（cv_results_陣列的索引）。

優化Titanic生存預測程式碼

  在上一篇部落格中，我使用決策樹和k-NN兩種分類器對處理後的Titanic數據集進行了分類預測，其中k-NN分類器的training set score爲0.82，test set score爲0.72，還有一部分優化空間。下面 下麪用網格搜尋和交叉驗證進行調參。

# 使用GridSearchCV進行調參
from sklearn.model_selection import GridSearchCV

knn = KNeighborsClassifier()
param_grid = [
    {
        'weights': ['uniform'],
        'n_neighbors': [i for i in range(1, 11)]
    },
    {
        'weights': ['distance'],
        'n_neighbors': [i for i in range(1, 11)],
        'p': [i for i in range(1, 6)]
    }
]
grid_search = GridSearchCV(knn, param_grid, n_jobs=-1, verbose=2)

%%time
grid_search.fit(X_train, y_train)

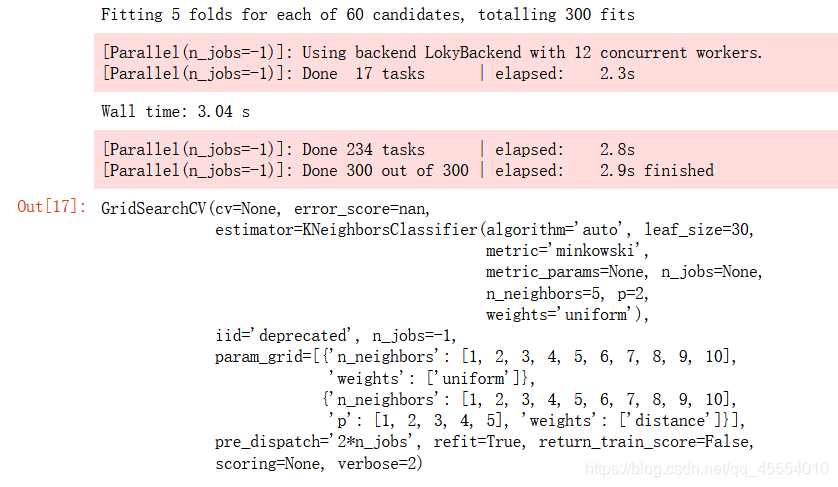
  接下來檢視一下GridSearchCV的屬性。

# 最優超參數組合對應的分類器
grid_search.best_estimator_

# 最優超參數組合
grid_search.best_params_

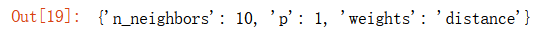
# 最優超參數組合對應的準確率
grid_search.best_score_

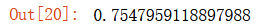
  最後我們使用最優的分類器模型對測試集進行預測。

knn = grid_search.best_estimator_
y_predict = knn.predict(X_test)
print(y_predict)
print('Training set score: {:.2f}'.format(knn.score(X_train, y_train)))
print('Test set score: {:.2f}'.format(knn.score(X_test, y_test)))

  可以看出training set score有了明顯的提升（從0.82提升到0.98），但是test set score的提升不是很多（從0.72提升到0.73）。