拓撲排序(C語言)

拓撲排序使用的是廣度優先遍歷
要求：圖中沒有環
給定一個圖 選出一個沒有入度的點 作爲起始點 之後 將這個點從圖中刪除 並且以該點爲入度的點要-1
[圖片選自數據結構與演算法分析© P229 圖9-4]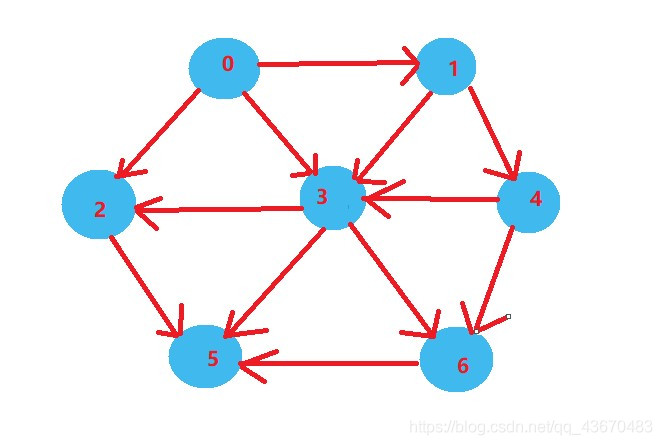
如上圖 第一次存取0點 並且將0點從圖中刪除 並且將與之相鄰的點的入度減1 如果存在入度爲0的點 則選擇 那麼這裏能夠選擇的點是 1 依次類推 直到選擇完 如果無法選擇點 那麼圖中就存在環 就無法使用拓撲排序

使用的鄰接表+佇列
首先定義出鄰接表和佇列的結構

#define MAX  10
#define WHITE 0 // 未存取
#define BLACK 1 // 已經存取
typedef int bool;
// 鄰接表實現對有向圖的儲存
typedef struct Node Node;
typedef struct Node* Vertex;
typedef struct Node* adjustlist;
struct Node {
	int visit; // 用來標記是否存取
	int item; // item用來記錄標號
	int indegree; // 入度
	int outdegree; // 出度
	struct Node* next; // 指向下一個節點
};
typedef struct queue queue;
typedef struct queue* pqueue;
typedef pqueue* ppqueue; // 指向佇列節點的指針
struct queue
{
	adjustlist vertex;   //指向 鄰接表的節點的指針
	struct queue* next;  // 指向佇列的下一個元素
};

上面寫出了的WHITE 和BLACK 是後續廣度優先遍歷的時候 用來記錄點是否已經存取 防止多次存取

生成鄰接鏈表和初始化賦值鄰接表

// 生成一個鄰接表
static adjustlist createadjustlist(int vertex)
{
	// vertex 是圖的頂點
	// 假定 圖的頂點都是從0開始到vertex
	adjustlist ad = (adjustlist)malloc(sizeof(Node) * vertex);
	if (ad == NULL)
	{
		printf(" Out of space\n");
		return NULL;
	}
	// 順便初始化
	for (int i = 0; i < vertex; i++)
	{
		ad[i].visit = ad[i].item = ad[i].indegree = ad[i].outdegree = 0;
		ad[i].next = NULL;
	}
	return ad;
}

static void initialadjustlist(adjustlist ad, int vertex)
{
	for (int i = 0; i < vertex; i++)
	{ // 圖頂點從0開始
		int k, v, u;  // v 用來確定出度  u用來確定入度 k表示標號
		scanf("%d %d %d", &k, &v, &u); // 確定每一個點的出度  出度表明這個頂點到那幾個點
		ad[k].item = k;
		ad[k].indegree = u; // 入度
		ad[k].outdegree = v; // 出度
		for (int j = 0; j < v; j++)
		{
			adjustlist V = (adjustlist)malloc(sizeof(Node));
			if (V == NULL)
			{
				printf("Out of space\n");
				return;
			}
			scanf("%d", &V->item); // 確定後續得節點是什麼
			// 使用頭插法
			V->next = ad[k].next;
			ad[k].next = V;
		}
	}
}

關於後續節點的儲存 我使用的是新生成一個鄰接節點 然後儲存 實際上由於是數位節點 可以在鄰接節點中使用 int陣列或者指針 實現儲存 這個大家可以去實現一下

佇列的建立

static pqueue createqueue()
{
	// 構造一個佇列 實際上就是一個鏈表 所以並不需要大小
	// 但是 使用頭結點 第一個節點用於空出來
	pqueue Q = (pqueue)malloc(sizeof(queue));
	if (Q == NULL)
	{
		printf(" Out of space\n");
		return NULL;
	}
	Q->next = NULL;
	Q->vertex = NULL;
	return Q;
}

佇列的方法 加入 刪除 釋放

static pqueue Enqueue(adjustlist V, pqueue tail)
{   // tail 指向生成的佇列Q的末尾
	pqueue q = createqueue();
	q->vertex = V;
	tail->next = q;
	tail = tail->next;
	return tail;
}

static adjustlist dequeue(pqueue head, ppqueue tail)
{
	// 也要變換tail指針內容
	pqueue q = head->next; // head是頭結點 實際上是無法儲存數據 也就是從head.next開始儲存數據
	head->next = head->next->next;
	if (q == *tail)
	{ // 說明 佇列中只有一個元素 並且要刪除它
		*tail = head; // 將其指向 head
	}
	adjustlist ad = q->vertex;
	free(q);
	return ad;
}

static bool IsEmpty(pqueue head)
{  // 判斷佇列是否爲空
	return head->next == NULL;
}

static void freequeue(pqueue Q)
{
	pqueue head = Q;
	pqueue p;
	while (head->next != NULL)
	{
		p = Q->next;
		head->next = Q->next->next;
		free(p);
	}
	free(head);
}

拓撲排序和展示

static int path[MAX] = { 0 };

static void Topsort(adjustlist ad, int vertex)
{
	pqueue Q = createqueue(); // 建立的一個佇列
	pqueue head = Q;
	pqueue tail = head;
	for (int i = 0; i < vertex; i++)
		if (ad[i].indegree == 0)
		{
			tail = Enqueue(&ad[i], tail);
			// 此時將加入的點標記成存取狀態
			ad[i].visit = BLACK;
		}
	int counter = 0;
	while (!IsEmpty(Q))
	{
		adjustlist V = dequeue(Q, &tail);
		path[V->item] = ++counter; // 記錄下路徑的存取順序
		adjustlist tmp = V;
		for (int i = 0; i < V->outdegree; i++) // 遍歷出度 表示有多少的後繼
		{
			int t = tmp->next->item; // 選取第一個
			adjustlist T = &(ad[t]);  // 固定下標從0開始 所以 item也就是剛好在ad陣列的相應位置上
			if (T->visit == BLACK)
				continue;
			T->indegree--;
			if (T->indegree == 0)
				tail = Enqueue(&ad[t], tail); // 如果T的入度爲0 則加入佇列中
			tmp = tmp->next;
		}
	}
	if (counter != vertex)
	{
		printf(" Graph have a cirecle\n");
		return;
	}
	//銷燬佇列
	freequeue(Q);
}

static void showpath(int vertex)
{
	for (int i = 0; i < vertex; i++)
	{
		printf("%d\t", path[i]);
	}
	printf("\n");
}

static void showgraph(adjustlist ad, int vertex)
{
	for (int i = 0; i < vertex; i++)
	{
		printf("頂點%d\t", ad[i].item);
		adjustlist T = ad[i].next;
		for (int j = 0; j < ad[i].outdegree; j++)
		{
			printf("後繼是%d\t", T->item);
			T = T->next;
		}
		printf("\n");
	}
}

主方法

void main()
{
	int n;
	scanf("%d", &n);
	adjustlist ad = createadjustlist(MAX); // MAX 給定的最大範圍
	initialadjustlist(ad, n);
	showgraph(ad, n);
	Topsort(ad, n);
	showpath(n);
}

結果

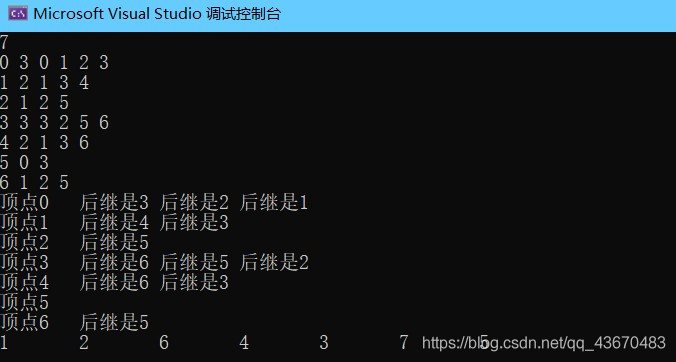
輸入
7
0 3 0 1 2 3
1 2 1 3 4
2 1 2 5
3 3 3 2 5 6
4 2 1 3 6
5 0 3
6 1 2 5

(有錯誤請在下方指出，輕噴)