淺析平衡二元樹、AVL樹、紅黑樹

淺析平衡二元樹、AVL樹、紅黑樹

平衡二元樹

​ 在瞭解紅黑樹之前，首先要瞭解一下什麼是平衡二元樹。平衡樹(Balance Tree，BT) 指的是，一 棵空樹或它的左右兩個子樹的高度差的絕對值不超過1，並且左右兩個子樹也都是一棵平衡二元樹。

平衡的四種類型：

LL型：在左子樹的左孩子上插入元素；解決辦法:(左旋) 如下圖：

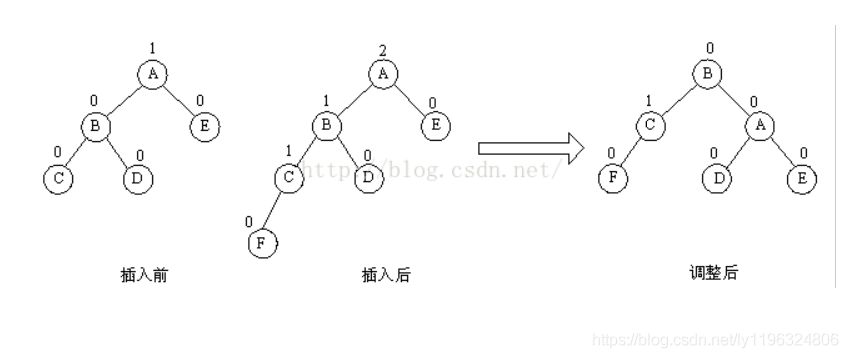
RR型：在右子樹的右孩子上插入元素；解決辦法（右旋）如下圖：

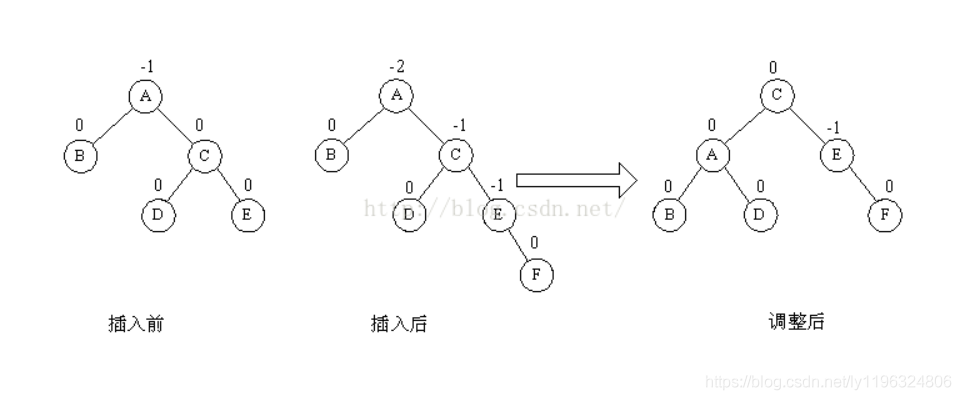
RL型：在右子樹的左孩子上插入元素；解決辦法（先右旋再左旋） 如下圖：

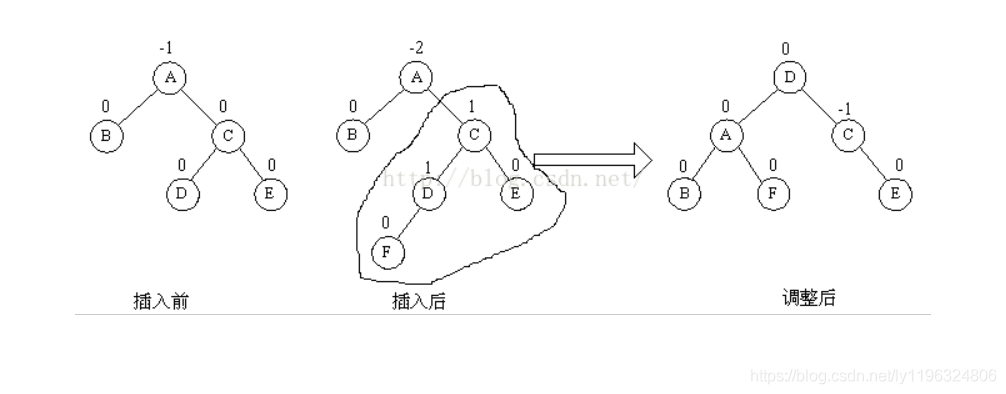
LR型：在左子樹的右孩子上插入元素；（先左旋再右旋）

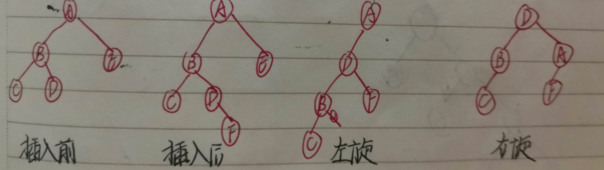
紅黑樹

​ 紅黑樹就是一種特殊的平衡二元樹，那麼他就存在着平衡二元樹的特點，同時他也存在自己特有的特點。相對一般的平衡二元樹來說，他在基本的平衡二元樹中新增了着色（紅色和黑色）和相關的一些性質，使得紅黑樹平衡。

紅黑樹具體具有的特徵：

• 性質1.結點存在顏色（只能是紅和黑）；
• 性質2.根節點必須是黑色；
• 性質3.每個葉子結點（指樹尾端的NULL或者NIL結點）是黑色的；
• 性質4.每個紅色結點的子結點必須爲黑色（不能兩個紅色結點相連，可以兩個黑色相連）；
• 性質5.對任意結點而言，它到子樹的葉節點尾端NIL指針的路徑包含相同數目的黑結點。

紅黑樹新增元素的情況以及實現平衡

​ 插入過程首先是根據一般二叉查詢樹的插入步驟， 把新節點 z 插入到 某個葉節點的位置上，然後將 z 着 爲紅色。 爲了保證紅黑樹的性質能繼續保持，再對有關節點重點着色並旋轉，（以左子樹爲例）其插入情況如下：

• 第一種情況：當前爲一顆空樹，我們插入的結點爲根節點，
  此時插入爲根節點，但是和性質2 違背，所以這時候，我們的對策就是直接將這個結點改爲黑色就可以了。
• 第二種情況：插入的結點的父節點爲黑色，這時候就可以直接插入結點。
• 第三種情況：父節點爲紅色，且祖父結點的另外一個子節點（叔結點）也是紅色。此時插入結點，會造成兩個紅色結點相連。與性質4相違背。
  這時候我們就將父節點和叔結點都改爲黑色，並且將祖父結點改爲紅色（將兩個同時設定爲黑色，且祖父結點設定爲紅是爲了保證性質5）。
• 第四種情況：當前結點的父節點爲紅色，其叔結點爲黑色，當前結點爲父節點的右結點。此時我們將當前結點的父節點爲新的當前結點，以型的當前結點左旋。
• 第五種情況：當前結點的父節點爲紅色，其叔結點爲黑色，當前結點爲父節點的左結點。此時我們將當前結點的父節點變爲黑色，祖父結點變爲紅色，祖父結點爲支點右旋。

​ 一般來說，第四、第五種情況都是在第三種情況後的插入修復操作，所以我們可以將第三，四，五種情況當做一種完整的插入修復的操作流程。

應用範圍：

1. 廣泛用於C ++的STL中，地圖是用紅黑樹實現的;
2. Linux的的進程排程，用紅黑樹管理過程控制塊，進程的虛擬記憶體空間都儲存在一顆紅黑樹上，每個虛擬記憶體空間都對應紅黑樹的一個節點，左指針指向相鄰的虛擬記憶體空間，右指針指向相鄰的高地址虛擬記憶體空間;
3. IO多路複用的epoll採用紅黑樹組織管理sockfd，以支援快速的增刪改查;
4. Nginx中用紅黑樹管理定時器，因爲紅黑樹是有序的，可以很快的得到距離當前最小的定時器;
5. Java的TreeMap的實現;

AVL樹

​ AVL樹是帶有平衡條件得二叉查詢樹，也是最早被髮明得自平衡二叉查詢樹，在AVL樹中，任一節點對應的兩棵子樹的最大高度差爲1，因此它也被稱爲高度平衡樹，所以它必須滿足平衡條件。

AVL樹失衡與重平衡

AVL樹的失衡的兩種情況：

1. 由新節點插入導致：新節點的插入可能導致很多祖先節點的失衡，但是經過一次旋轉就能把所有的失衡節點全都回覆 回復。插入導致的失衡有以下兩種情況情況

   情況1：單旋解決

   

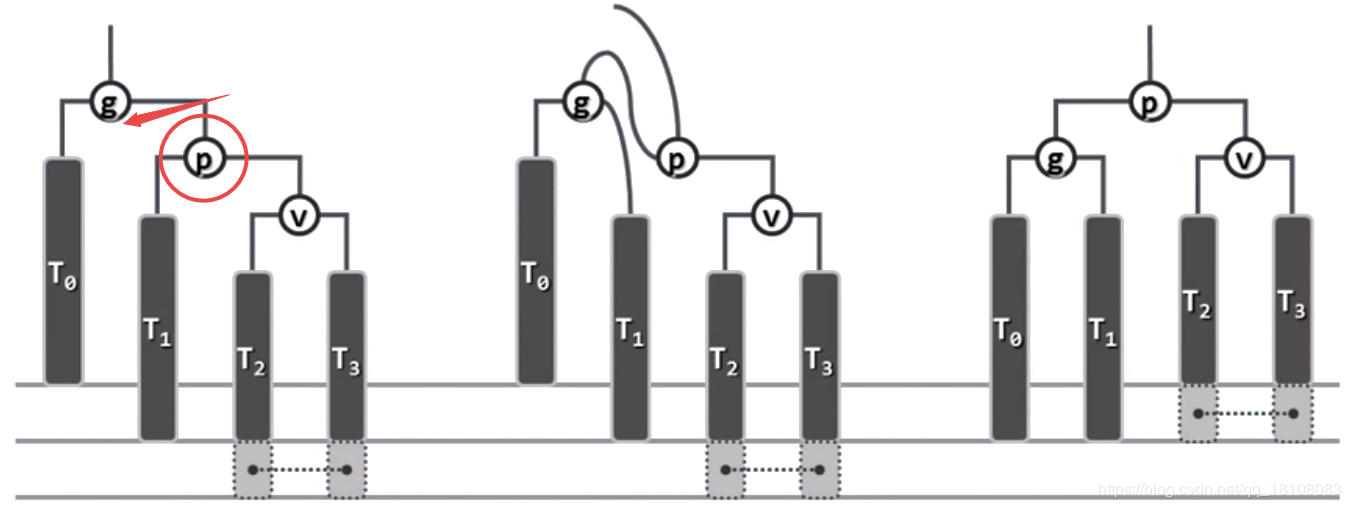
   情況2：雙旋解決

   

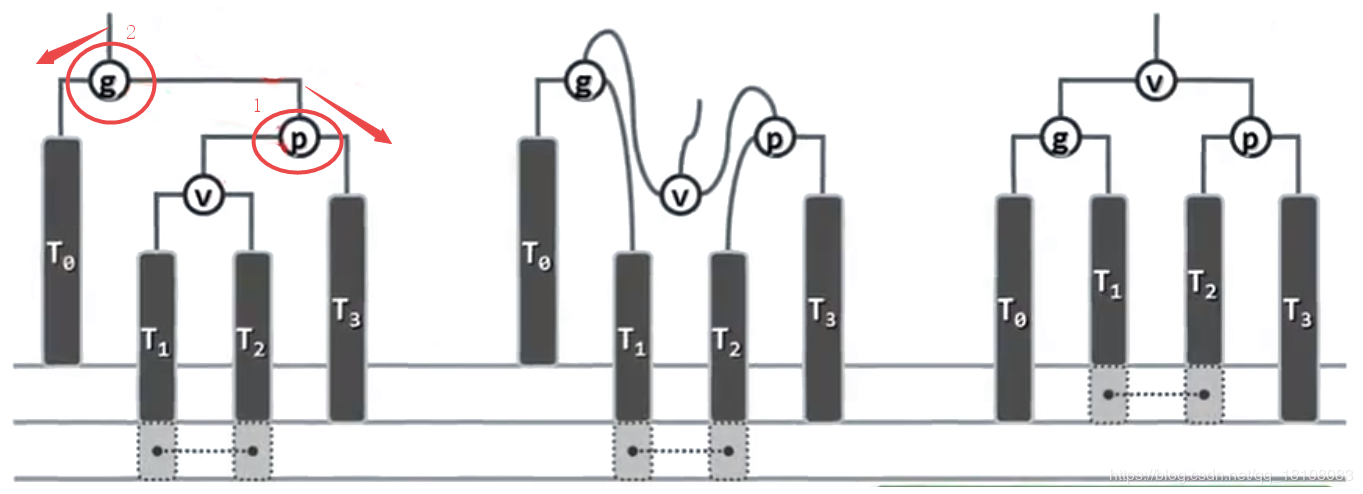
2. 由節點刪除導致：節點的刪除只會導致一個祖先節點的失衡，但是在節點恢復的時候可能導致新的祖先節點的失衡，而且這種情況在每一層都出現，所以需要逐層向上檢查並旋轉恢復。刪除導致的失衡也有如下兩種情況：

   情況1：單旋解決

   

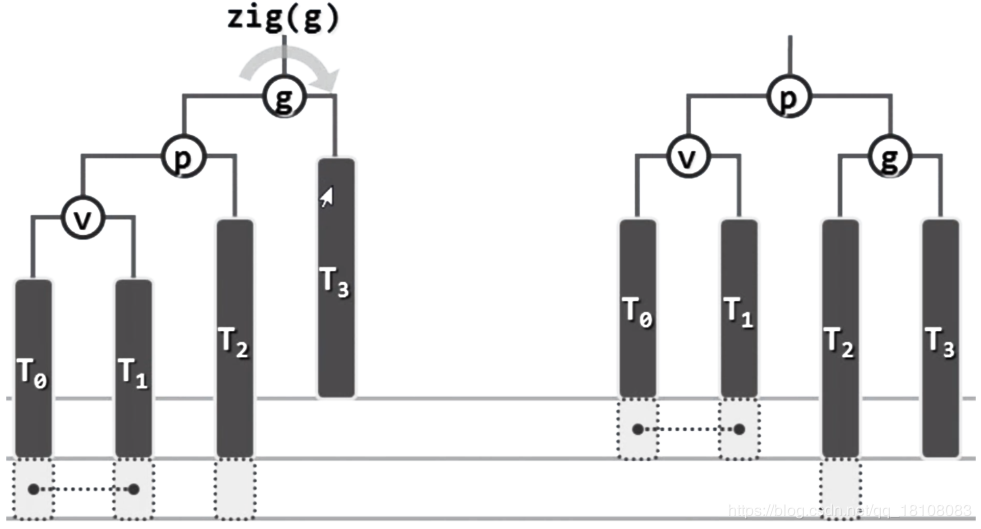
   情況2：雙旋解決

   

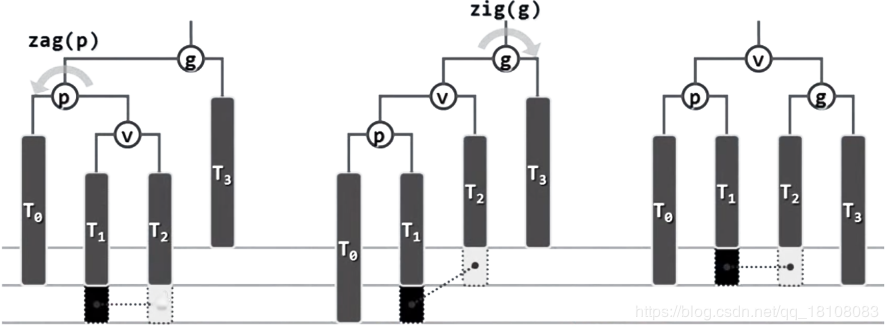
AVL樹的效能

優點：

• 無論查詢、插入或者刪除，最壞情況下的複雜度均爲O(logn)，O(n)的儲存空間。

缺點：

• 藉助高度或者平衡因子，所以需要改造元素結構，或者額外封裝這一屬性。
• 插入或刪除後的旋轉成本高，刪除操作後，最多要旋轉logn次(一般5次操作發生一次這種情況)，所以頻繁插入刪除成本高。
• 單次動態調整後，全樹拓撲結構的變化量可能高達longn，這在實際的應用中是很避諱的。

AVL樹與紅黑樹的比較：

1. 因爲相同節點的情況下AVL樹的高度會低於黑紅樹，因此在做查詢時AVL樹用的時間相對會少。
2. 在刪除和插入的時候，AVL樹由於具有高度平衡，而紅黑樹只是弱平衡，因此黑紅樹旋轉次數會遠小於AVL樹。
3. 紅黑樹在失衡的情況下恢復平衡比AVL樹快，因此紅黑樹有着良好的穩定性和完整的功能，效能表現也很不錯，綜合實力強。

總結：

AVL樹：平衡性高，失衡恢復時間長因此穩定性差，易查詢不易刪除插入。

紅黑樹：平衡性低，失衡恢復較快因此穩定性高，但樹長相對較高，查詢，刪除，插入都比較方便。

參考：https://blog.csdn.net/u010899985/article/details/80981053

參考：https://blog.csdn.net/qq_18108083/article/details/84932582