數據結構和演算法——學習筆記

第1章 數據結構緒論

1.1基本概念和術語

1、數據：是描述客觀事物的符號，是計算機中可以操作的物件，是能被計算機識別，並輸入給計算機的符號集合。
2、數據元素：是組成數據的、有一定意義的基本單位，在計算機中通常作爲整體處理。也被稱爲記錄。
3、數據項：一個數據元素可以由若幹個數據項組成。數據項是數據不可分割的最小單位。
4、數據物件：是性質相同的數據元素的集合，是數據的子集。
5、數據結構：是相互之間存在一種或多種特定關係的數據元素的集合。

1.2邏輯結構與物理結構

1、邏輯結構：是指數據物件中數據元素之間的相互關係。
（1）集合結構：集合結構中的元素除了同屬於同一個集合外，它們之間沒有其他關係。
（2）線性結構：線性結構中的數據元素之間是一對一的關係。
（3）樹形結構：樹形結構是數據元素之間存在一種一對多的層次關係。
（4）圖形結構：圖形結構的數據元素是多對多的關係。
2、物理結構：是指數據的邏輯結構在計算機中的儲存形式。
（1）順序儲存結構；；是把數據元素存放在地址連續的儲存單元中，其數據間的邏輯關係和物理關係是一致的。
（2）鏈式儲存結構：是把數據元素存放在任意的儲存單元裡，這組儲存單元可以是連續的，也可以是不連續的。

1.3抽象數據型別

1、數據型別：是指一組性質相同的值得集合及定義在此集合上的一些操作的總稱。
2、在C語言中，按照取值的不同，數據型別可以分爲兩類：
（1）原子型別：是不可以再分解的基本型別，包括整型、實型、字元型等。
（2）結構型別：由若幹型別組合而成，是可以再分解的。例如，整型陣列是由若幹整型數據組成的。
3、抽象是指抽取出事物的普遍性的本質。
4、抽象數據型別（ADT）：是指一個數據模型及定義在該模型上的一組操作。
5、「抽象」的意義在於數據型別的屬性抽象特性。抽象數據型別體現了數據程式設計中問題分解、抽象和資訊隱藏的特性。
6、描述抽象數據型別的標準格式：

ADT 抽象數據型別名
Data
	數據元素之間的邏輯關係的定義
Operation
	操作1
		初始條件
		操作結果描述
	操作2
		……
	操作n
		……
endADT

第2章 演算法

2.1演算法定義

1、演算法是解決特定問題求解步驟的描述，在計算機中表現爲指令的有限序列，並且每條指令表示一個或多個操作。

2.2演算法的特性

1、輸入輸出：演算法具有零個或多個輸入，演算法至少有一個或多個輸出。
2、有窮性：指演算法在執行有限的步驟之後，自動結束而不會出現無限回圈，並且每個步驟在可接受的時間內完成。
3、確定性：演算法的每一步驟都具有確定的意義，不會出現二義性。
4、可行性：演算法每一步驟都必須是可行的，也就是說，每一步都能夠通過執行有限次數完成。

2.3演算法設計的要求

1、正確性：演算法的正確性是指演算法至少應該具有輸入、輸出和加工處理無歧義性、能正確反映問題的需求、能夠得到問題的正確答案。
2、可讀性：演算法的設計的另一目的是爲了便於閱讀，理解和交流。
3、健壯性：但數據數據不合法時，演算法也能做出相關處理，而不是產生異常或莫名其妙的結構。
4、時間效率高和儲存量低：設計演算法應儘量滿足時間效率高和儲存量的需求。

2.4演算法效率的度量方法

1、事後統計方法
2、事前分析估算方法

2.5算的時間複雜度定義

1、在進行演算法分析時，語句總的執行次數T(n)是關於問題規模n的函數，進而分析T(n)隨n的變化情況並確定T(n)的數量及。演算法的時間複雜度，也就是演算法的時間量度，記作：T(n)=O(f(n))。它表示隨問題規模n的增大，演算法執行時間的增長率和f(n)的增長率相同，稱爲演算法的漸進時間複雜度，簡稱爲時間複雜度。其中f(n)問題規模n的某個函數。
2、大O記法：用大寫O()來體現演算法的時間複雜度的記法。
3、推導大O階方法：
（1）用常數1取代執行時間中額所有加法常數。
（2）在修改後的執行次數函數中，只保留最高階項。
（3）如果最高階項存在且不是1，則去除與這個項相乘的常數。

2.6常見的時間複雜度

執行次數函數	階	非正式術語
12	O(1)	常數階
2n+3	O(n)	線性階
3n2+2n+1	O(n2)	平方階
5log2n+20	O(logn)	對數階
2n+3nlog2n	O(nlogn)	nlogn階
6n3+2n2+3n+4	O(n3)	立方階
2n	O(2n)	指數階

常見的時間複雜度所耗費時間從小到大依次是：

O(1)<O(logn)<O(n)<O(nlogn)<O(n²)<O(n³)<O(2ⁿ)<O(n!)<O(nⁿ)

2.7最壞情況與平均情況

1、最壞情況執行時間是一種保證，那就是執行時間將不會在壞了。在應用中，這是一種最重要的需求，通常，除非特別指定，我們提到的執行時間都是最壞情況的執行時間。
2、平均執行時間是所有情況中最有意義的，，因爲它是期望的執行時間。
3、一般在沒有特殊說明的情況下，都是最壞時間複雜度。

2.8演算法空間複雜度

1、演算法的空間複雜度通過計算演算法所需的儲存空間實現，演算法空間複雜度的計算公式記作：S(n)=O(f(n))，其中，n爲問題的對魔，f(n)爲語句關於n所佔儲存空間的函數。
2、通常，我們都是使用「時間複雜度」來指執行時間的需求，使用「空間複雜度」指空間需求。當不用限定地使用「複雜度」時，通常是指時間複雜度。

第3章 線性表

3.1線性表的定義

1、線性表(List)：零個或多個數據元素的有限序列。
2、數學語言定義：若線性表記爲(a1,……,a_i-1,a_i,a_i+1,……,a_n)，則表中a_i-1領先於a_i,a_i領先於a_i+1，稱a_i-1是a_i的直接前驅元素，a_i+1是a_i的直接後繼元素。當i=1，2，3，……，n-1是a_i有且僅有一個直接後繼，當i=2，3，……，n是，a_i有且僅有一個直接前驅。
3、空表：線性表元素的個數n(n>=0)定義爲線性表的長度，當0時，成爲空表

3.2線性表的抽象數據型別

線性表的抽象數據型別定義如下：

ADT 線性表(List)
Data
	線性表是數據物件集合爲{a1,a2,……,an},每個元素的型別均爲DataType。其中，除第一個元素a1外，每一個元素有且只有一個直接前驅元素，除了最後一個元素an外，每一個元素有且只有一個直接後繼元素。數據元素之間的關係是一對一的關係。
Operation
	InitList(*L);	初始化操作，建立一個空的線性表L。
	ListEmpty(L);	若線性表爲空，返回true，否則返回false。
	ClearList(*L);	將線性表清空。
	GetElem(L,i,*e);	將線性表L中的第i個位置的元素值返回給e。
	LocateElem(L,e);	線上性表L中查詢與給定值e相等的元素，如果查詢成功，返回該元素在表中的序號表示成功；否則，返回0表示失敗。
	ListInsert(*L,i,e);	線上性表L中的第i個位置插入新元素e。
	ListDelete(*L,i,*e);	刪除線性表L中第個i個位置元素，並用e返回其值。
	ListLength(L);	返回線性表L的元素個數。
endADT

實現兩個線性表集合A和B的操作。

/*將所有的線上性表Lb中但不在La中的數據元素插入到La中*/
void union(List *La,List *Lb)
{
	int La_len,Lb_len,i;
	ElemType e;	/*宣告與La和Lb相同的數據元素e*/
	La_len = ListLength(La);	/*求線性表的長度*/
	Lb_len = ListLength(Lb);
	for(i=1; i<Lb_len; i++)
	{
		GetElem(Lb, i, e);	/*取出Lb中第i個數據元素賦值給e*/
		if(!LoacteElem(La,e)) /*La中不存在和e相同數據元素*/
			ListInsert(La, ++La_len, e);	/*插入*/
	}
}

3.3線性表的順序儲存結構

1、順序儲存定義：線性表的順序儲存結構，指的是用一段連續的儲存單元依次儲存線性表的數據元素。
2、順序儲存方式：可以用C語言的一維陣列來實現順序儲存結構。
線性表的順序儲存結構程式碼。

	#define MAXSIZE 20	/*儲存空間初始分配量*/
	typedef ine ElemType;	/*ElemType型別根據實際情況而定，這裏假設爲int*/
	typedef struct
	{
		ElemType data[MAXSIZE];	/*陣列儲存數據元素，最大值爲MAXSIZE*/
		int length;	/*線性表當前長度*/
	}SqList;

3、陣列長度與線性表長度的區別
（1）陣列的長度是存放線性表的儲存空間的長度，儲存分配後這個量是一般不變的。
（2）線性表的長度是線性表中的元素個數，隨着線性表插入和刪除操作的進行，這個量是變化的。
（3）在任何時刻，線性表的長度應該小於等於陣列的長度。
4、地址計算方法
（1）線性表的數是從1開始數的，可C語言中的陣列確實從0開始第一個下標的，於是線性表的第i個元素是要儲存在陣列下標爲-1的位置。
（2）記憶體中每個儲存單元都有自己的編號，這個編號稱爲地址。
（3）假設每個數據元素佔用的是c個儲存單元，那麼線性表中的第i+1個數據元素的儲存位置和第i個數據的儲存位置滿足下列關係

	LOC(a(i+1))=LOC(ai)+c

所以對於第i個數據元素ai的儲存位置可以有a1推算得出：

	LOC(ai)=LOC(ai)+(i-1)*c

5、存取結構：分爲隨機存取和非隨機存取（又稱順序存取）
（1）隨機存取就是直接存取，可以通過下標直接存取的那種數據結構與儲存結構位置無關，例如陣列。
（2）非隨機存取就是順序存取，不能通過下標存取，只能按照儲存順序存取，與儲存位置有關，例如鏈表。
（3）順序存取就是存取第N個數據時，必須先存取前（N-1）個數據 （list），隨機存取就是存取第N個數據時，不需要存取前（N-1）個數據，直接就可以對第N個數據操作 （array）。
（3）順序表是順序儲存，隨機存取的結構； 鏈表是隨機儲存，順序存取的結構； 注意儲存和存取的區別。

3.4順序儲存結構的插入和刪除

1、獲得元素操作

	#define OK 1
	#define ERROR 0
	#define TRUE 1
	#define FLASE 0
	typedef int Status;
	/*Status是函數的型別，其值是函數結果狀態程式碼，如OK等*/
	/*初始條件：順序線性表已存在，1<=i<=ListLength(L)*/
	/*操作條件：用e返回L中第i個數據元素的值*/
	Status GetElem(SqList L,int i, ElemType *e)
	{
		if(L.length==0 || i<1 || i>L.length)
			return ERROR;
		*e=L.data[i-1];
		return OK;
	}

2、插入操作
插入演算法的思路：
（1）如果插入位置不合理，拋出異常；
（2）如果線性表長度大於陣列長度，則拋出異常或動態增加容量；
（3）從最後一個元素開始向前遍歷到第i個位置，分別將它們都向後移動一個位置；
（4）將要插入的元素填入位置i處；
（5）表長加1.
實現程式碼如下：

/*初始條件：順序線性表L已存在，1<=i<=ListLength(L)*/
/*操作結果：在L中第i個位置之前插入新的數據元素e，L的長度加1*/
Status ListInsert(Sqlist *L,int i,ElemType e)
{
	int k;
	if(L->length==MAXSIZE) /*順序線性表已滿*/
		return ERROR;
	if(i<1 || i>L->length+1)	/*當i不在範圍內時*/
		return ERROR;
	if(i<=L->length)	/*若插入數據位置不在表尾*/
	{
		for(k=L->length-1;k>=i-1;k--) /*將要插入位置後的數據元素向後移動一位*/
			L->data[k+1]=L->data[k];
	}
	L->data[i-1]=e; /*將新元素插入*/
	L->length++;
	return OK;
}

3、刪除操作
刪除演算法的思路：
（1）如果刪除位置不合理，拋出異常；
（2）取出刪除元素；
（3）從刪除元素位置開始遍歷到最後一個元素位置，分別將它們都向前移動一個位置；
（4）表長減1。
實現程式碼如下：

/*初始條件：順序線性表L已存在，1<=i<=ListLength(L)*/
/*操作結果：刪除L中第i個位置的數據元素，並用e返回其值，L的長度減1*/
Status ListDelete(Sqlist *L,int i,ElemType *e)
{
	int k;
	if(L->length==0) /*順序線性表爲空*/
		return ERROR;
	if(i<1 || i>L->length)	/*刪除位置不正確*/
		return ERROR;
	*e=L->data[i-1];
	if(i<L->length)	/*如果刪除不是最後位置*/
	{
		for(k=i;k<L->length;k++) /*將刪除位置後繼元素前移*/
			L->data[k-1]=L->data[k];
	}
	L->length--;
	return OK;
}

4、線性表順序儲存結構的優缺點
優點：
（1）無需爲表中元素之間的邏輯關係而增加額外的儲存空間；
（2）可以快速地存取表中任一位置的元素。
缺點：
（1）插入和刪除操作需要移動大量元素；
（2）當線性表長度變化較大時，難以確定儲存空間的容量；
（3）造成儲存空間的「碎片」。

3.5線性表的鏈式儲存結構

1、數據域，指針域，結點
爲了表示每個數據元素a_i與其直接連線後繼數據元素a_i+1之間的邏輯關係，對數據元素a_i來說，除了儲存其本身的資訊之外，還需儲存一個指示其直接後繼的資訊（即直接後繼的儲存位置）。我們把儲存數據元素資訊的域稱爲數據域，把儲存直接後繼位置的域稱爲指針域。指針域中儲存的資訊稱作指針或鏈。這兩部分資訊組成數據元素a_i的儲存映像，稱爲結點（Node）。
2、單鏈表
n個結點（a_i的儲存映像）鏈結成一個鏈表，即爲線性表（a₁，a₂，……，a_n）的鏈式儲存結構，因此此鏈表的每個結點中只包含一個指針域，所以叫單鏈表。線性鏈表的最後一個結點指針爲「空」（通常用NULL或「^」符號表示）。
3、頭指針
鏈表中第一個結點的儲存位置叫做頭指針。
4、頭結點
單鏈表的第一個結點前附設一個結點，稱爲頭結點。頭結點可以不儲存任何資訊，也可以儲存如線性表長度等附加資訊，頭結點的指針域儲存指向第一個結點的指針。

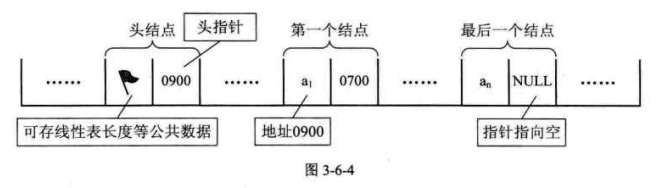
5、頭指針與頭結點的異同
頭指針
（1）頭指針是指指向第一個結點的指針，若鏈表有頭結點，則是指向頭結點的指針。
（2）頭指針具有表示作用，所有常用頭指針冠以鏈表的名字。
（3）無論鏈表是否爲空，頭指針均不爲空。頭指針是鏈表的必要元素。
頭結點
（1）頭結點是爲了操作的統一和方便而設立的，放在第一元素的結點之前，其數據域一般無意義（也可存放鏈表的長度）。
（2）有了頭結點，對在第一元素結點前插入結點和刪除第一結點，其操作與其它結點的操作就統一了。
（3）頭結點不一定是鏈表必須要素。
6、若線性表爲空表，則頭結點的指針域爲「空」

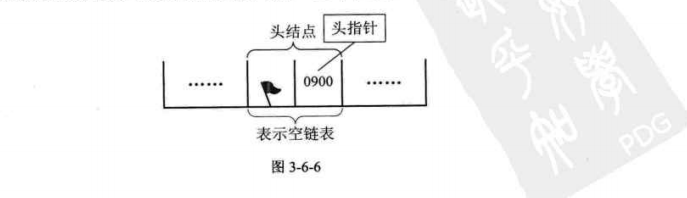
儲存示意圖表示單鏈表

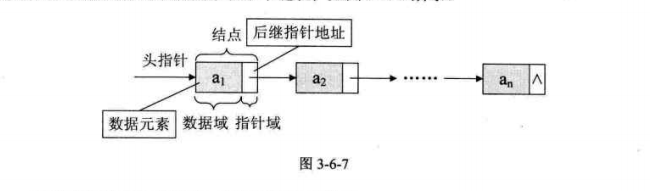
若帶有頭結點的單鏈表

空鏈表

7、單鏈表中，C語言中可用結構指針來描述

/*線性表的單鏈表儲存結構*/
typedef struct Node
{
	ElemType data;
	struct Node *next;
}Node;
typedef struct Node *LinkList; /*定義LinkList*/

結點由存放數據元素的數據域存放後繼結點地址的指針域組成。

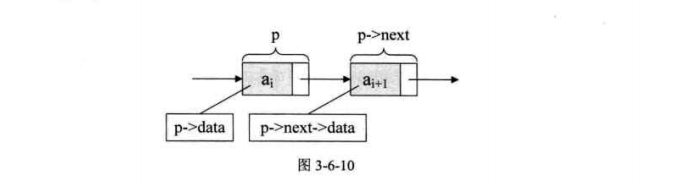
3.6單鏈表的讀取

單鏈表實現獲取第i個元素的數據的操作GetElem，單鏈表的結構中沒有定義表長，不能事先知道要回圈多少次，其主要核心思想是「工作指針後移」。
獲得鏈表第i個數據的演算法思路：
1、宣告一個結點p指向鏈表的第一個結點，初始化j從1開始；
2、當j<i時，就遍歷鏈表，然p的指針移動，不斷指向下一結點，j累加1；
3、若到鏈表末尾p爲空，則說明第i個元素不存在；
4、否則查詢成功，返回結點p的數據。
實現程式碼演算法如下：

/*初始條件：順序線性表L已存在*，1<=i<=ListLength(L)*/
/*操作結果：用e返回L中第i個數據元素的值*/
Status GetElem(LinkList L,int i,ElemType *e)
{
	int j;
	LinkList p;	/*宣告一結點p*/
	p=L->next;	/*讓p指向鏈表L的第一個結點*/
	j=1;	/*j爲計數器*/
	while(p&&j<i)	/*p不爲空或者計數器j還沒有等於i時，回圈繼續*/
	{
		p=p->next;	/*讓p指向下一個結點*/
		++j;
	}
	if(!p||j>i)
		return ERROR;	/*第i個元素不存在*/
	*e=p->data;	/*取第i個元素的數據*/
	return OK;
}

3.7單鏈表的插入和刪除

1、單鏈表的插入
單鏈表第i個數據插入結點的演算法思路：
（1）宣告一結點p指向鏈表的第一個結點，初始化j從1開始；
（2）當j<i時，就遍歷鏈表，讓p的指針向後移動，不斷指向下一結點，j累加1；
（3）若到鏈表末尾p爲空，則說明第i個元素不存在；
（4）否則查詢成功，在系統中生成一個空結點s;
（5）將數據元素e賦值給s->data;
（6）單鏈表的插入標準語句s->next=p->next, p->next=s;
（7）返回成功。
實現程式碼演算法如下：

/*初始條件：順序線性表L已存在，1<=i<=ListLength(L)*/
/*操作結果：在L中第i個位置之前插入新的數據元素e，長度加1*/
Status ListInsert(LinkList *L,int i,ElemType e)
{
	int j;
	LinkList p,s;
	p=*L;
	j=1;
	while(p&&j<i)	/*尋找第i個結點*/
	{
		p=p->next;
		++j;
	}
	if(!p||j>i)
		return ERROR;	/*第i個元素不存在*/
	s=(LinkList)malloc(sizeof(Node));	/*生成新結點*/
	s->data=e;
	s->next=p->next;	/*將p的後繼結點賦值給s的後繼*/
	p->next=s;	/*將s賦值給p的後繼*/
	return OK;
}

2、單鏈表的刪除
單鏈表第i個數據刪除結點的演算法思路：
（1）宣告一結點p指向鏈表第一個結點，初始化j從1開始；
（2）當j<i時，就遍歷鏈表，讓p的指針向後移動，不斷指向下一個結點，j累加1；
（3）若到鏈表末尾p爲空，則說明第i個元素不存在；
（4）否則查詢成功，將欲刪除的結點p->next賦值給q；
（5）單鏈表的刪除標準語句p->next=q->next;
（6）將q結點中的數據賦值給e，作爲返回；
（7）釋放q結點；
（8）返回成功。
實現程式碼演算法如下：

/*初始條件：順序線性表L已存在，1<=i<=ListLength(L)*/
/*操作結果：刪除L的第i個數據元素，並用e返回其值，L的長度減1*/
Status ListDelete(LinkList *L,int i,ElemType *e)
{
	int j;
	LinkList p,q;
	p=*L;
	j=1;
	while(p->next&&j<i)	/*遍歷尋找第i個元素*/
	{
		p=p->next;
		++j;
	}
	if(!(p->next)||j>i)
		return ERROR;	/*第i個元素不存在*/
	q=p->next;	
	p->next=q->next;	/*將q的後繼賦值給p的後繼*/
	*e=q->data;	/*將q結點中的數據給e*/
	free(q);	/*讓系統回收此結點，釋放記憶體*/
	return OK;
}

3.8單鏈表的整表建立

單鏈表整表建立的演算法思路：
1、宣告一結點p和計數器變數i；
2、初始化一空鏈表L；
3、讓L的頭結點的指針指向NULL，即建立一個帶頭結點的單鏈表；
4、回圈：
（1）生成一新結點賦值給p；
（2）隨機生成一數位賦值給p的數據域p->data；
（3）將p插入到頭結點與前一新結點之間。
頭插法：

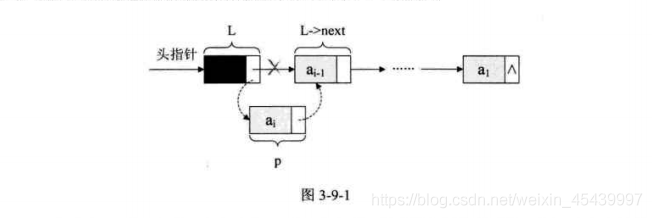
/*隨機產生n個元素的值，建立帶有頭結點的單鏈線性表L（頭插法）*/
void CreateListHead(LinkList *L,int n)
{
	LinkList p;
	int i;
	srand(time(0)); /*初始化亂數種子*/
	*L=(LinkList)malloc(sizeof(Node));
	(*L)->next=NULL; /*先建立一個帶頭結點的單鏈表*/
	for(i=0;i<n;i++)
	{
		p=(LinkList)malloc(sizeof(Node));	/*生成新結點*/
		p->data=rand()%100+1;
		p->next=(*L)->next;
		(*L)->next=p;	/*插入到表頭*/
	}
}

尾插法：

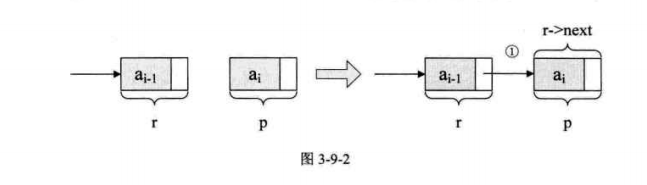
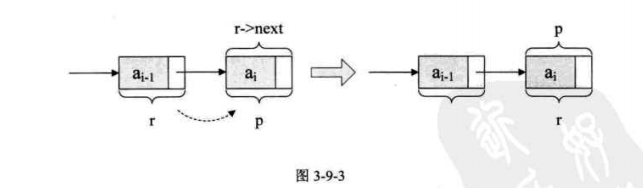
/*隨機產生n個元素的值，建立帶表頭結點的單鏈線性表L（尾插法）*/
void CreateListTail(LinkList *L,int n)
{
	LinkList p,r;
	int i;
	srand(time((0));
	*L=(LinkList)malloc(sizeof(Node));
	r=*L;	/*r爲指向尾部的結點*/
	for(i=0;i<n;i++)
	{
		p=(Node *)malloc(sizeof(Node));	/*生成新結點*/
		p->data=rand()%100+1;	/*隨機生成100以內的數位*/
		r->next=p;	/*將表尾終端結點的指針指向新結點*/
		r=p;	/*將當前的新結點定義爲表尾終端結點*/
	}
	r->next=NULL;	/*表示當前鏈表結束*/
}

3.9單鏈表的整表刪除

單鏈表整表刪除的演算法思路如下：
1、宣告一結點p和q；
2、將第一個結點賦值給p；
3、回圈：
（1）將下一個結點賦值給q;
（2）釋放p；
（3）將q賦值給p。
實現程式碼演算法如下：

Status ClearList(LinkList *L)
{
	LinkList p,q;
	p=(*L)->next;	/*p指向第一個結點*/
	while(p)	/*沒到表尾*/
	{
		q=p->next;
		free(p);
		p=q;
	}
	(*L)->next=NULL; /*頭結點指針域爲空*/
	return OK;
}

3.10單鏈表結構與順序儲存結構優缺點

1、若線性表需要頻繁查詢，很少進行插入操作時，宜採用順序儲存結構。若需要頻繁插入和刪除時，宜採用單鏈表結構。
2、當線性表中的元素個數變化較大或者根本不知道有多大時，最好用單鏈表結構，這樣可以不用考慮儲存空間問題。而如果事先知道線性表的大致長度，這種使用者順序儲存結構效率會高很多。

3.11靜態鏈表

1、靜態鏈表（遊標實現法），用陣列來代替指針描述的鏈表叫做靜態鏈表。首先我們讓陣列的元素都是由兩個數據域組成，data和cur。也就是說，陣列的每一個下標都對應一個data和一個cur。數據域data，用來存放數據元素，也就是通常我們要處理的數據；而遊標cur相當於單鏈表中的next指針，存放該元素的後繼在陣列中的下標。

/*線性表的靜態鏈表儲存結構*/
#define MAXSIZE 1000	/*假設鏈表的最大長度1000*/
typedef struct
{
	ElemType data;
	int cur;	/*遊標，爲0是表示無指向*/
}	Component,StaticLinkList(MAXSIZE);

2、對陣列第一個和最後一個元素作爲特殊元素處理，不存數據。通常把未使用的陣列稱爲備用鏈表。而陣列第一元素，即下標爲0的元素的cur就存放備用鏈表中的第一個結點的下標；而陣列最後一個元素的cur則存放第一個有數值的元素的下標，單鏈表中的頭結點作用，當整個鏈表爲空時，則爲0。

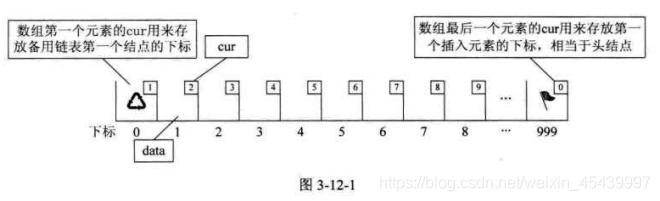
此時圖示相當於初始化的陣列狀態，見下面 下麪程式碼：

/*將一維陣列space中各分量鏈成一備用鏈表*/
/*space[0].cur 爲頭指針，"0"表示空指針*/
Status InitList(StaticLinkList space)
{
	int i;
	for(i=0;i<MAXSIZE-1;i++)
		space[i].cur=i+1;
	space[MAXSIZE-1].cur=0;	/*目前靜態鏈表爲空，最後一個元素的cur爲0*/
	return OK;
}

3、靜態鏈表的插入操作
靜態鏈表中藥解決的是：如何用靜態模擬動態鏈表結構的儲存空間的分配，需要是時申請，無用時釋放。
爲了辨明陣列中哪些分量未被使用，解決的辦法是將所有未使用過的及已被刪除的分量用遊標鏈成一個備用的鏈表，每當進行插入時，便可以從備用鏈表上取得第一個結點爲待插入的新結點。

/*若備用空間鏈表非空，則返回分配的結點下標，否則返回0*/
int Malloc_SLL(StaticLinkList space)
{
	int i=spacep[0].cur;	/*當前數據第一元素的cur存的值，就是要返回的第一個備用空閒的下標*/
	if(space[0].cur)
		space[0].cur=space[i].cur;	/*由於要拿出一個分量來使用了，所以我們就得把它的下一個分量用來做備用*/
	return i;
}

Status LinkInsert(StaticLinkList L,int i,ElemType e)
{
	int j,k,l;
	k=MAX_SIZE-1;	/*注意k首先是最後一個元素的下標*/
	if(i<1||i>ListLength(L)+1)
		return ERROR;
	j=Malloc_SSL(L);	/*獲得空閒分量的下標*/
	if(j)
	{
		L[j].data=e;	/*將數據賦值給此分量的data*/
		for(l=1;l<i-1;l++)	/*找到第i個元素之前的位置*/
			k=L[k].cur;
		L[j].cur=L[k].cur	/*把第i個元素之前的cur賦值給新元素的cur*/
		L[k].cur=j;	/*把新元素的下標賦值給第i個元素之前元素的cur*/
		return OK;
		
	}
	return ERROR;
}

4、靜態鏈表的刪除操作

/*刪除在L中第i個數據元素e*/
Status ListDelete(StaticLinkList L,int i)
{
	int j,k;
	if(i<1||i>ListLength(L))
		return ERROR;
	k=MAX_SIZE-1;
	for(j=1;j<=i-1;j++)
		k=L[k].cur;
	j=L[k].cur;
	L[k].cur=L[j].cur;
	Free_SSL(L,j);
	return OK;
}

/*將下標爲k的空閒結點回收到備用鏈表*/
void Free_SSL(StaticLinkList spcace,int k)
{
	space[k].cur=space[0].cur;	/*把第一個元素cur值賦給要刪除的分量cur*/
	space[0].cur=k;	/*把要刪除的分量下標賦值給第一個元素的cur*/
}

5、靜態鏈表的長度

/*初始條件：靜態鏈表L已存在。操作結果：返回L中數據元素個數*/
int ListLength(StaticLinkList L)
{
	int j=0;
	int i=L(MAXSIZE-1).cur;
	while(i)
	{
		i=L[i].cur;
		j++;
	}
	return j;
}

3.12回圈鏈表

1、將單鏈表中終端結點的指針端由空指針改爲指向頭指針，就使整個單鏈表形成一個環，這種頭尾相接的單鏈表稱爲單回圈鏈表，簡稱回圈鏈表
2、回圈鏈表帶頭結點的空鏈表

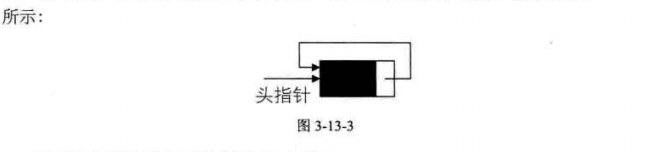
3、對於非空的回圈鏈表

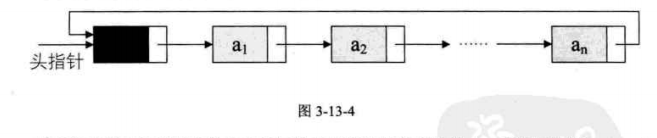
4、回圈鏈表和單單鏈表的主要差異就在於回圈的判斷條件上，原來是判斷p->next是否爲空，現在則是p->next不等於頭結點，則回圈未結束。
5、將兩個回圈鏈表合併成一個表時，下面 下麪兩個回圈鏈表的尾指針分別是rearA和rearB。

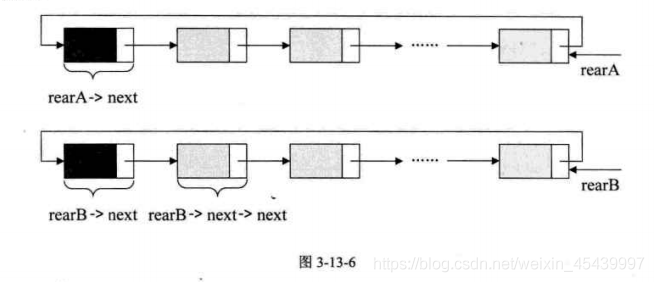
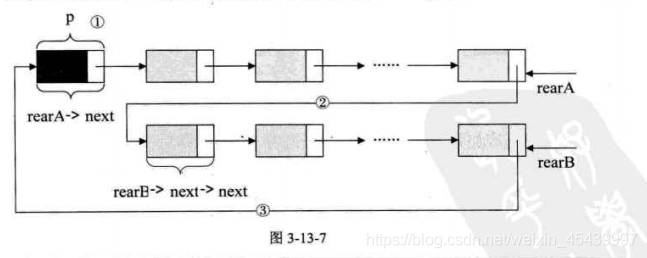
p=rearA->next;	/*儲存A表的頭結點*/
rearA->next=rearB->next->next;	/*將本是指向B表的第一個結點（不是頭結點，賦值給rearA->next）*/
rearB->next=p;	/*將原A表的頭結點賦值給rearB->next*/
free(p);	/*釋放p*/

3.12雙向鏈表

1、雙向鏈表是在單鏈表的每個結點中，再設定一個指向其前驅結點的指針域。

/*線性表的雙向鏈表儲存結構*/
typedef struct DulNode
{
	ElemType data;
	struct DulNode *prior;	/*直接前驅指針*/
	struct DulNode *next;	/*直接後繼指針*/
}DulNode,*DuLinkList;

第4章 棧與佇列

4.1 棧的定義

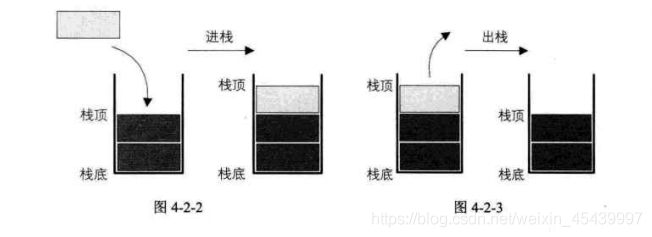
1、棧是限定僅在表尾進行插入和刪除操作的線性表。
2、允許插入和刪除的一端稱爲棧頂，另一端稱爲棧底，不含任何數據元素的棧稱爲空棧。棧又稱爲後進先出（Last In First Out）的線性表，簡稱LIFO結構。
3、棧的插入操作，叫作進棧，也稱壓棧、入棧。
4、棧的刪除操作，叫作出棧，也有的叫作彈棧。

4.2 棧的抽象數據型別

ADT 棧(stack)
Data
	同線性表。元素具有相同的型別，相鄰元素具有前驅和後繼關係。
Operation
	InitStack(*S):初始化操作，建立一個空棧S。
	DestroyStack(*S):若棧存在，則銷燬它。
	ClearStack(*S):將棧清空。
	StackEmpty(S):若棧爲空，返回true，否則返回false。
	GetTop(*S,e):若棧存在且非空，用e返回S的棧頂元素。
	Push(*S,e):若棧S存在，插入新元素e到棧S中併成爲棧頂元素。
	Pop(*S,*e):刪除S中棧頂元素，並用e返回其值。
	StackLength(S):返回棧S的元素個數。
endADT

4.3 棧的順序儲存結構及實現

1、棧的順序儲存結構

typedef int SElemType;	
typedef struct
{
	SElemType data[MAXSIZE];
	int top;	/*用於棧頂指針*/
}SqlStack;

若現在有一個棧，StackSize是5，則棧普通情況、空棧和棧滿的情況：

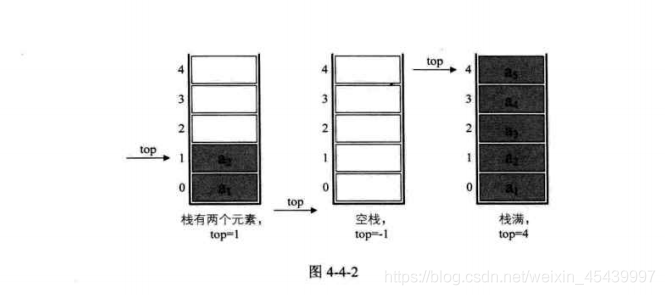
2、棧的順序儲存結構——進棧操作

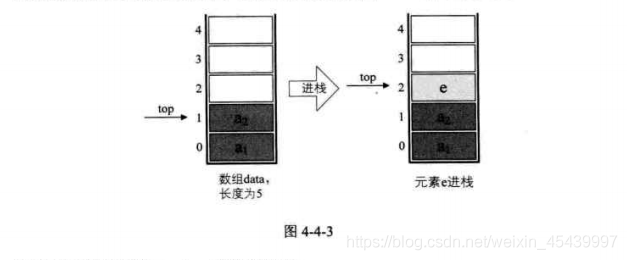
/*插入元素e爲新的棧頂元素*/
Status Push(SqStack *s, SElemType e)
{
	if(S->top == MAXSIZE-1) /*棧滿*/
	{
		return ERROR;
	}
	S->top++;	/*棧頂指針加1*/
	S->data[S->top]=e;	/*將新插入元素賦值給棧頂元素*/
	return OK;
}

3、棧的順序儲存結構——出棧操作

/*若棧不空，則刪除S的棧頂元素，用e返回其值，並返回OK，否則返回ERROR*/
Status Pop(SqStack *S, SElemType *e)
{
	if(S->top == -1)
	{
		return ERROR;
	}
	*e=S->data[S->top];	/*將要刪除的棧頂元素賦值給e*/
	S->top--;	/*棧頂指針加一*/
	return OK;
}

4.4 兩棧共用空間

1、陣列有兩個端點，兩個棧有兩個棧底，讓第一個棧的棧底爲陣列的始端，即下標爲處，另一個棧爲棧的末端，即下標陣列長度n-1處。這樣兩個棧如果增加元素，就是兩端點向中間延伸。

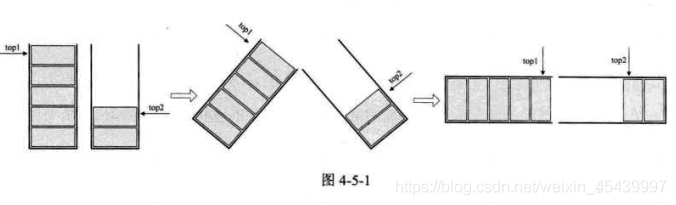
兩棧共用空間的結構的程式碼：

/*兩棧共用空間結構*/
typedef struct
{
	SElemType data[MAXSIZE];
	int top1; /*棧1棧頂指針*/
	int top2; /*棧2棧頂指針*/
}SqDoubleStack;

對於兩棧共用空間的push方法，我們除了要插入元素值參數外，還需要判斷是棧1還是棧2的棧號參數stackNumber。插入元素的程式碼如下：

/*插入元素e爲新的棧頂元素*/
Status Push(SqDouble *S, SElemType e, int stackNumber)
{
	if(S->top1+1==S->top2)	/*棧已滿，不能再push新元素了*/
		return ERROR；
	if(StackNumber==1) /*棧1有元素進棧*/
		S->data[++S->top1]=e;	/*若棧1則先top1+1後給陣列元素賦值*/
	else if (StackNumber==2)	/*棧2有元素進棧*/
		S->data[--S->top2]=e;	/*若棧2則先top2-1後給陣列元素賦值*/
	return OK;
}

對於；兩棧共用空間的pop方法，參數就只判斷棧1棧2的參數stackNumber，程式碼如下：

/*若棧不空，則刪除S的棧頂元素，用e返回其值，並返回OK，否則返回ERROR*/
Status Pop (SqDoubleStack *S, SElemType *e, int stackNumber)
{
	if(stackNumber==1)
	{
		if(S->top1==-1)
			return ERROR; /*說明棧1已經是空棧，溢位*/
		*e=S->data[S->top1--];	/*將棧1的棧頂元素出棧*/
			
	}
	else if (stackNumber==2)
	{
		if(S->top2==MAXSIZE)
			return ERROR; /*說明棧2已經是空棧，溢位*/
		*e=S->data[S->top2++];	/*將棧2的棧頂元素出棧*/
	}
	return OK;
}

4.5 棧的鏈式儲存結構及實現

1、棧的鏈式儲存結構，簡稱爲鏈棧。
對於空棧來說，鏈表原定義是頭指針指向空，那麼鏈棧的空其實就是top=NULL的時候。
鏈棧的結構程式碼如下：

typedef struct StackNode
{
	SElemType data;
	struct StackNode *next;
}StackNode, *LinkStackPtr;

typedef struct LinkStack
{
	LinkStackPtr top;
	int count;
}LinkStack;

2、棧的鏈式儲存結構——進棧操作
對於鏈棧的進棧push操作，假設元素值爲e的新結點是s,top爲棧頂指針。

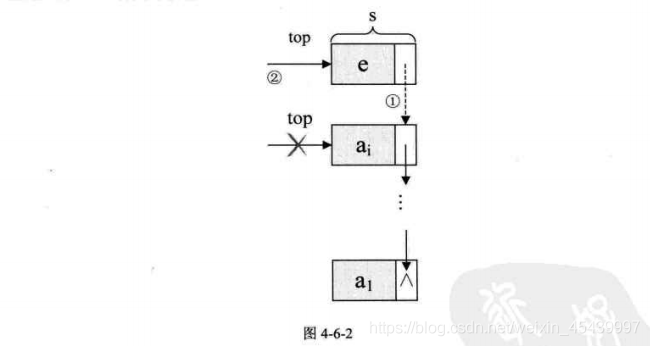
/*插入元素e爲新的棧頂元素*/
Status Push(LinkStack *S, SElemType e)
{
	LinkStackPtr s = (LinkStackPtr)malloc(sizeof(StackNode));
	s->data=e;
	s->next=S->top;
	S->top=s;
	S->count++;
	return OK;
} 

3、棧的鏈式儲存結構——出棧操作
至於鏈棧的出棧pop操作，也是簡單的三句操作。假設變數p用來儲存要刪除的棧頂結點，將棧頂指針下移一位，最後釋放p即可。

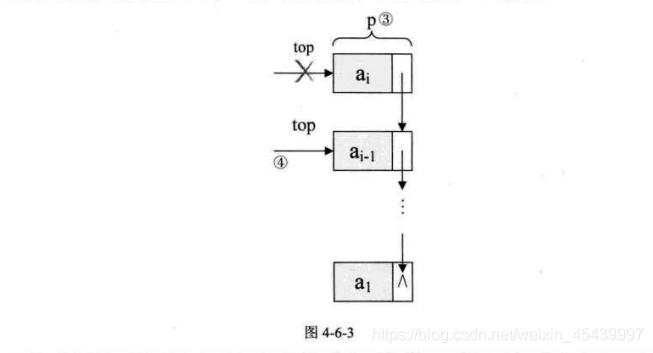
/*若棧不空，則刪除S的棧頂元素，用e返回其值*/
Status Pop(LinkStack *S, SElemType *e)
{
	LinkStackPtr p;
	if(StackEmpty(*S))
		return ERROR;
	*e=S->top->data;
	p=S->top;	/*將棧頂元素賦值給p*/
	S->top=S->top->next;	/*使得棧頂指針下移一位，指向後一結點*/
	free(p);	/*釋放結點p*/
	S->count--;
	return OK;
}

4、如果棧的使用過程中元素變化不可預料，有時很小，有時非常大，那麼最好是用鏈棧，反之，它的變化在可控範圍內，建議使用順序棧會更好一些。

4.6 棧的應用——遞回

1、斐波那契數列實現
列印出前40位斐波那契數列數
（1）常規的迭代實現

int main()
{
	int i;
	int a[40];
	a[0]=0;
	a[1]=1;
	printf("%d ",a[0]);
	printf("%d ",a[1]);
	for(i=2;i<40;i++)
	{
		a[i] = a[i-1] + a[i-2];
		printf("%d ",a[i]);
	}
	return 0;
}

（2）遞回實現

/*斐波那契的遞回函數*/
int Fbi(int i)
{
	if(i<2)
		return i == 0 ? 0 : 1;
	return Fbi(i-1) + Fbi(i-2);
}
int main()
{
	int i;
	for(i=0; i<40; i++)
	{
		printf("%d ", Fbi(i));
	}
	return 0;
}

2、遞回定義
（1）把一個直接呼叫自己或通過一系列的呼叫語句間接地呼叫自己的函數，稱作遞回函數。
（2）每個遞回定義必須至少有一個條件，滿足時遞回不再進行，即不再參照自身而是返回值退出。
（3）遞回和迭代的區別是：迭代使用的是回圈結構，遞回使用的是選擇結構。

4.7 棧的應用——四則運算表達式求值

1、後綴（逆波蘭）表示法定義
一種不需要括號的後綴表達式，對於「9+(3-1)×3+10÷2」，用後綴表示法應該是「9 3 1 - 3 * + 10 2 / +」，這樣的表達式稱爲後綴表達式，叫後綴的原因在於所有的符號都是在要運算數位的後面出現。
2、後綴表達式的計算結果
規則：從左到右遍歷表達式的每個數位和符號，遇到的是數位就進棧，遇到的是符號，就將處於棧頂的兩個數位出棧，進行運算，執行結果進棧，一直到最終獲得結果。
3、中綴表達式轉後綴表達式
（1）標準四則運算表達式叫做中綴表達式。
（2）中綴表達式「9+(3-1)×3+10÷2」轉化爲後綴表達式「9 3 1 - 3 * + 10 2 / +」。
（3）規則：從左到右遍歷中綴表達式的每個數位和符號，若是數位就輸出，即成爲後綴表達式的一部分；若是符號，則判斷其與棧頂符號的優先順序，是右括號或優先順序低於棧頂符號（乘除優先加減）則棧頂元素依次出棧並輸出，並將當前符號進棧，一直到最終輸出後綴表達式爲止。

4.8 佇列的定義和抽象數據型別

1、佇列是隻允許在一端進行插入操作，而在另一端進行刪除操作的線性表。
2、佇列是一種先進先出（First In First Out）的線性表，簡稱FIFO。允許插入的一端稱爲隊尾，允許刪除的一端稱爲隊頭。

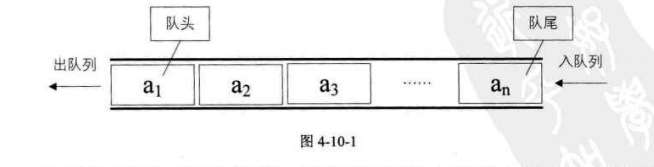
3、佇列的抽象數據型別
同樣是線性表，佇列也有類似線性表的各種操作，不同的就是插入數據只能在隊尾進行，刪除數據只能在隊頭進行。

ADT 佇列(Queue)
Data
	同線性表。元素具有相同的型別，相鄰元素具有前驅和後繼關係。
Operation
	InitQueue(*Q):初始化操作，建立一個空佇列Q。
	DestroyQueue(*Q):若佇列Q存在，則銷燬它。
	ClearQueue(*Q):將佇列Q清空。
	QueueEmpty(Q):若佇列Q爲空，則返回true，否則返回false。
	GetHead(Q,*e):若佇列Q存在且非空，用e返回佇列Q的隊頭元素。
	EnQueue(*Q,e):若佇列Q存在，插入新元素e到佇列Q中併成爲隊尾元素。
	DeQueue(*Q,*e):刪除佇列Q中隊頭元素，並用e返回其值。
	QueueLength(Q):返回佇列Q的元素個數
endADT

4.9 回圈佇列

1、佇列順序儲存的不足
假設一個佇列有n個元素，則順序儲存佇列需建立一個大於n的陣列，並把佇列的所有元素儲存在陣列的前n個單元，陣列下標爲0的一端即是隊頭。

入佇列操作是在隊尾追加一個元素，不需要移動任何元素，因此時間複雜度爲O(1)。

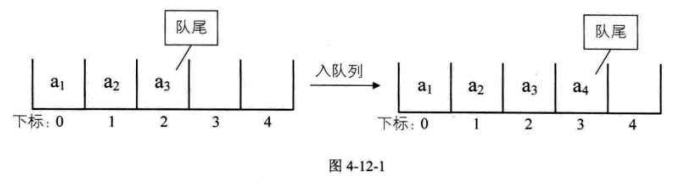
佇列元素的出列是在隊頭，即下標0的位置，佇列中所有的元素都得向前移動，以保證佇列的隊頭，也就是下標爲0的位置不爲空，此時時間複雜度爲O(n)。

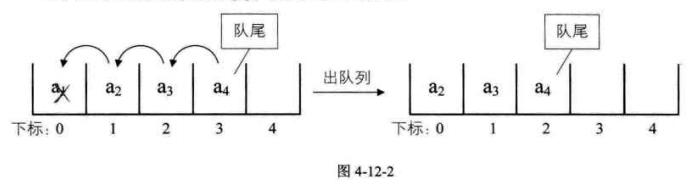
如果不去限制佇列元素必須儲存在陣列的前n個單元這一條件，出隊的效能就大大增加。隊頭不需要一定在下表爲0的位置。

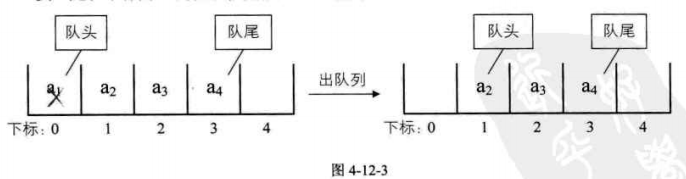
爲了避免當只有一個元素是，隊頭和隊尾重合使處理變得麻煩，所以引入兩個指針，front指針指向隊頭元素，rear指針指向隊尾元素的下一個位置，這樣當front等於rear時，此佇列不是還剩一個元素，而是空佇列。

假設是長度爲5的陣列，初始狀態，front與rear指針均指向下標爲0的位置。然後入隊a1,a2,a3,a4,front指針依然指向下標爲0的位置，而rear指針指向下標爲4的位置。

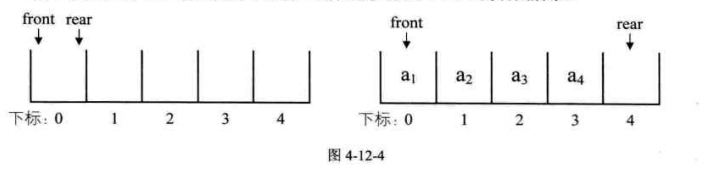
出隊a1,a2,則front指針指向下標爲2的位置，rear不變。再入對a5，此時front指針不變，rear指針移動到陣列之外。

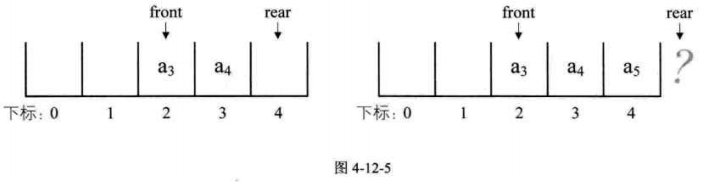
假設這個佇列的總個數不超過5個，但目前如果接着入隊的話，因陣列末尾元素已經佔用，再向後加，就會產生陣列越界的錯誤，可實際上，我們的佇列在下標爲0和1的地方還是空閒的，這種現象叫做「假溢位」。
2、回圈佇列定義
所以解決假溢位的辦法就是後面滿了，就再從頭開始，也就是頭尾相接的回圈。我們把佇列這種頭尾相接的順序儲存結構稱爲回圈佇列。

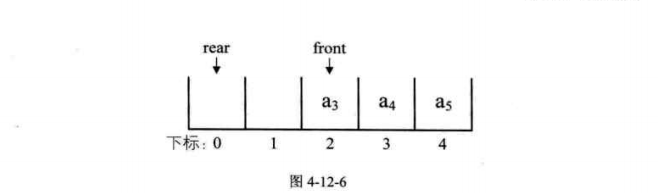
接着入隊a6，將它放置與下標0處，rear指針指向下標爲1處，若再入隊a7，則rear指針就與front指針重合，同時指向下標爲2的位置。

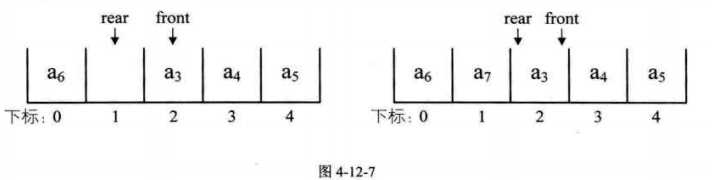
空佇列時，front等於rear，現在當佇列滿時，也是front等於rear。判斷佇列是空還是滿：
（1）設定一個標誌變數
（2）當佇列滿時，修改其條件，保留一個元素空間。佇列滿時，陣列中還存有一個空閒單元。

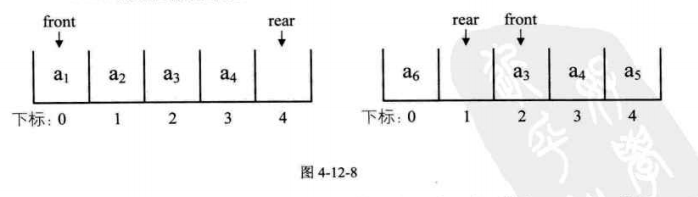
由於rear可能比front大，也可能比front小，所以儘管它們相差一個位置是就是滿的情況，但也可能是相差整整一圈。所以佇列的最大尺寸爲QueueSize,那麼佇列滿的條件是(rear+1)%QueueSize == front。

另外，當rear>front時，此時佇列的長度爲rear-front。但當rear<front時，佇列長度分別分爲兩段，一段是QueueSize-front，另一段是0+rear，加在一起rear-front+QueueSize，因此通用的計算佇列長度公式爲：
(rear-front+QueueSize)%QueueSize。

回圈佇列的順序儲存結構程式碼如下：

typedef int QElemType;/*QElemType型別根據實際情況而定，這裏假設爲int*/
/*回圈佇列的順序儲存結構*/
typedef struct
{
	QElemType data[MAXSIZE];
	int front;	/*頭指針*/
	int rear;	/*尾指針，若佇列不空，指向佇列尾元素的下一位置*/
}SqQueue;

回圈佇列的初始化程式碼如下：

/*初始化一個空佇列*/
Status InitQueue(SqQueue *Q)
{
	Q->front=0;
	Q->rear=0;
	return OK;
}

回圈佇列求佇列長度程式碼如下：

/*返回Q的元素個數，也就是佇列的當前長度*/
int QueueLength(SqQueue Q)
{
	return (Q.rear-Q.front+MAXSIZE)%MAXSIZE;
}

回圈佇列的入隊操作程式碼如下：

/*若佇列未滿，則插入元素e爲Q新的隊尾元素*/
Status EnQueue(SqQueue *Q, QElemType e)
{
	if((Q->rear+1)%MAXSIZE == Q->front)	/*佇列滿的判斷*/
		return ERROR;
	Q->data[Q->rear]=e;	/*將元素e賦值給隊尾*/
	Q->rear=(Q->rear+1)%MAXSIZE;	/*rear指針向後移一位置，若到最後則轉到陣列頭部*/

	return OK
}

回圈佇列的出隊操作程式碼如下：

/*若佇列不空，則刪除Q中隊頭元素，用e返回其值*/
Status DeQueue(SqQueue *Q, QElemType *e)
{
	if(Q->front == Q->rear)	/*佇列空的判斷*/
		return ERROR;
	*e=Q->data[Q->front];	/*將隊頭元素賦值給e*/
	Q->front=(Q->front+1)%MAXSIZE;	/*front指針向後移一位置，若到最後則轉到陣列頭部*/

	return OK
}

4.10 佇列的鏈式儲存結構及實現

1、佇列的鏈式儲存結構，其實就是線性表的單鏈表，只不過它只能尾進頭出而已，我們把它簡稱爲鏈佇列。爲了操作上的方便，我們將隊頭指針指向鏈佇列的頭結點，而隊尾指針指向終端結點。

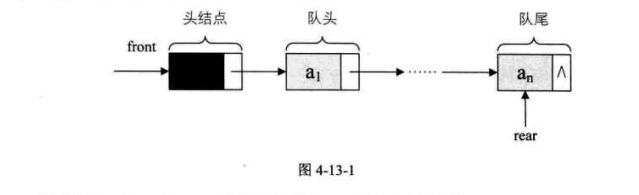
空佇列時，front和rear都指向頭結點。

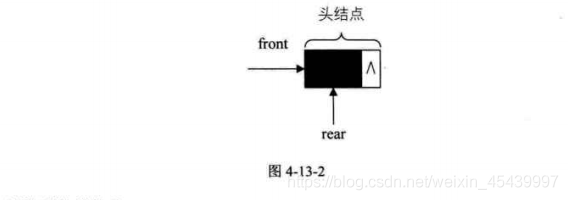
鏈佇列的結構爲：

typedef int QElemType;	/*QElemType型別根據實際情況而定，這裏假設爲int*/
typedef struct QNode	/*結點結構*/
{
	QElemType data;
	struct QNode *next;
	
}QNode, *QueuePtr;

typedef struct	/*佇列的鏈表結構*/
{
	QueuePtr front,rear; /*隊頭、隊尾指針*/
}LinkQueue;

2、佇列的鏈式儲存結構——入隊操作
入隊操作是，其實就是在鏈表尾部插入結點。

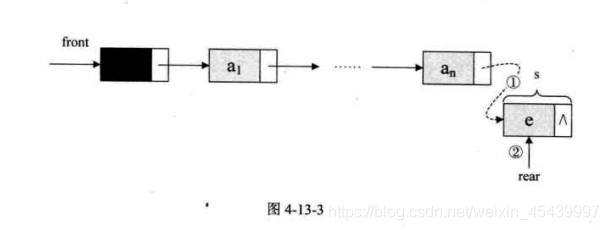
/*插入元素e爲新的隊尾元素*/
Status EnQueue(LinkQueue *Q, QElemType e)
{
	QueuePtr s=(QueuePtr)malloc(sizeof(QNode));
	if(!s)	/*儲存分配失敗*/
		exit(OVERFLOW);
	s->data=e;
	s->next=NULL;
	Q->rear->next=s;	/*把擁有元素e新結點s賦值給原隊尾結點的後繼*/
	Q->rear=s;	/*把當前的s設定爲隊尾結點，rear指向s*/
	return OK;
}

3、佇列的鏈式儲存結構——出隊操作
出隊操作時，就是頭結點的後繼結點出隊，將頭結點的後繼改爲它後面的結點，若鏈表除頭結點外只剩一個元素時，則需將rear指向頭結點。

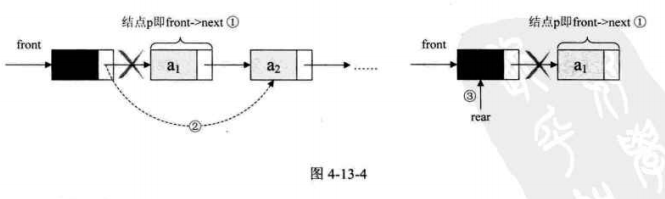
/*若佇列不空，刪除Q的隊頭元素，用e返回其值，並返回OK，否則返回ERROR*/
Status DeQueue(LinkQueue *Q, QElemType *e)
{
	QueuePtr p;
	if(Q->front==Q->rear)
		return ERROR;
	p=Q->front->next;	/*將欲刪除的隊頭結點暫存給p*/
	*e=p->data;	/*將欲刪除的隊頭結點的值賦給e*/
	Q->front->next=p->next;	/*將原隊頭結點後繼p->next賦值給頭結點後繼*/
	if(Q->rear==p)	/*若隊頭是隊尾，則刪除後將rear指向頭結點*/
		Q->rear=Q->front;
	free(p);
	return OK;
}

4、在可以確定佇列長度最大值的情況下，建議用回圈佇列，如果無法預估佇列的長度是，則用鏈佇列。

第5章 串

5.1 串的定義

1、串是由零個或多個字元組成的有限序列，又名叫字串。串中的字元數目稱爲串的長度。零個字元的串稱爲空串，它的長度爲零，可以直接用「 「」 」表示，也可以用希臘字母「Φ」表示。
2、空格串是隻包含空格的串，空格串是有內容有長度的，而且可以不止一個空格。
3、子串與主串，串中任意個數連續字元組成的字元序列稱爲該串的子串，相應的，包含子串的串稱爲主串。
4、子串在主串中的位置就是子串的第一個字元在主串中的序號。

5.2 串的比較

1、C語言中要比較兩個串是否相等，必須是它們串的長度以及它們各自對應位置的字元都相等時，纔算是相等。
2、給定兩個串：s=「a1a2a3……an」，t=「b1b2b3……bm」
（1）例如當s=「hap」， t=「happy」，就有s<t。因爲t比s多出了兩個字母。
（2）例如當s=「happen」，t=「happy」,因爲兩串的前4個字母相同，而兩串的第5個字母，字母e的ASCII碼是101，而字母y的ascii碼是121，顯然e<y，所以s<t。
（3）例如當s=「abc」，t="bc"時，s<t。

5.3 串的抽象數據型別

5.4 串的儲存結構

5.5 樸素的模式匹配演算法

5.6 KMP模式匹配演算法

第6章 樹

6.1 樹的定義

6.2 樹的抽象數據型別

6.3 樹的儲存結構

6.4 二元樹的定義

6.5 二元樹的性質

6.6 二元樹的儲存結構

6.7 遍歷二元樹

6.8 二元樹的建立

6.9 線索二元樹

6.10 樹、森林與二元樹的轉換

6.11 赫夫曼樹及其應用

第7章 圖

7.1 圖的定義

7.2 圖的抽象數據型別

7.3 圖的儲存結構

7.4 圖的遍歷

7.5 最小生成樹

7.6 最短路徑

7.7 拓撲排序

7.8 關鍵路徑

第8章 查詢

8.1 查詢概論

8.2 順序表查詢

8.3 有序表查詢

8.4 線性索引查詢

8.5 二叉排序樹

8.6 平衡二元樹（AVL樹）

8.7 多路查詢樹（B樹）

8.8 雜湊表查詢（雜湊表）概述

8.9 雜湊函數的構造方法

8.10 處理雜湊衝突的方法

8.11 雜湊表查詢實現

第9章 排序

9.1 排序的基本概念與分類

9.2 氣泡排序

9.3 簡單選擇排序

9.4 直接插入排序

9.5 希爾排序

9.6 堆排序

9.7 歸併排序

9.8 快速排序