名詞

離軌策略

允許函數以任意的目標策略作爲條件

折扣過程

12.8節中， 折扣過程 推廣爲 一個終止函數， 使得可以在每個時刻採用不同的折扣係數來作爲回報。

折扣係數

價值函數

廣義策略迭代（4.6節）或者「行動器一評判器」演算法

正文

17.1 廣義價值函數和輔助任務

1、廣義價值函數是什麼？

離軌策略允許函數以任意的目標策略作爲條件，終止函數的引入，使得可以在每個時刻採用不同的折扣係數來作爲回報。
允許我們在一個任意的、狀態相關的視界，可以預測未來能得到多少收益。

下一步：將收益推廣， 允許對任意信號的預測。

比如，聲音、顏色等信號未來的值之和進行預測， 而不止對未來的收益值之和進行預測。

不管我沒累加的是什麼信號， 我們都稱其爲 預測的累積量 ： 累計信號：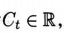

廣義價值函數GVF:

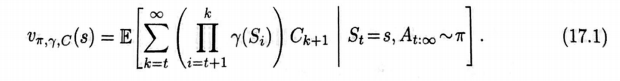
像傳統的價值函數（例如v或者q）一樣，這是一個可以用參數化的形式逼近的理想函數，我們可以繼續用v（s,w）來標記它，儘管對於每一種π、γ、Ct 的選擇，在每次預測過程中都會有一個不同的參數w。因爲一個GVF並不必然與收益有聯繫，因此將其稱爲值函數可能有些用詞不當。我們可以簡單地稱之爲「預測",或者用更獨特的方式說：預報（由Ring提出，準備發表）。不管如何稱呼它，它的形式都和價值函數一樣，因此可以用本書中提出的學習近似價值函數的方法學出來。在學習預測值的同時，我們也可以採用廣義策略迭代（4.6節）或者「行動器一評判器」演算法，通過最大化預測值來學習策略。用這種方式，一個智慧體可以學習如何預測和控制大量不同類型的信號，而不僅僅是長期收益。

爲什麼預測和控制長期收益之外的信號可能有用呢？這類信號控制任務是在最大化收益的主任務之外額外新增的輔助任務。一個答案是，預測和控制許多不同種類的信號可以構建一種強大的環境模型。正如我們在第8章所述，一個好的環境模型可以讓智慧體更高效地得到收益。清楚地回答這個問題需要一些其他的概念，我們將在下一節中介紹。首先我們考慮兩個相對簡單的方法，在這些方法中，多個不同種類的預測問題會對強化學習智慧體的學習有所幫助。

2、輔助任務是什麼？

輔助任務幫助主任務的一個簡單情形是它們可能需要一些相同的表徵。有些輔助任務可能更簡單，延遲更小，動作和結果之間的關聯關係更加明晰。如果在簡單的輔助任務中，可以很早發現好的特徵，那麼這些特徵可能會顯著地加速主任務的學習。沒有什麼理由可以解釋爲什麼這是對的，但是在很多情況下這看起來很有道理。例如，如果你學習在很短的時間內（例如幾秒鐘）預測和控制你的感測器，那麼你可能會想出這個目標物體的部分特點，這將對預測和控制長期收益有很大的幫助。

• 如果在簡單的輔助任務中，可以很早發現好的特徵，那麼這些特徵可能會顯著地加速主任務的學習。
• 如果你學習在很短的時間內（例如幾秒鐘）預測和控制你的感測器，那麼你可能會想出這個目標物體的部分特點，這將對預測和控制長期收益有很大的幫助。

我們可能會想象一個人工神經網路（ANN),其中的最後一層被分爲好幾個部分，我們稱它們爲頭部，每一個都在處理不同的任務。一個頭部可能產生主任務的價值函數預測（將收益作爲其累計量），而其他的頭部可能產生很多輔助任務的解。所有的頭部都可以通過隨機梯度下降法反向傳播誤差到同一個「身體」裡一即它們前面所共用的網路部分一從第二層到最後一層都在嘗試構建表示以提供必要的資訊給頭部。研究人員們嘗試了各種各樣的輔助任務，例如預測畫素的變化，預測下一時間點的收益，以及預測回報的概率分佈。在很多種情況下這個方法都顯示出了對主任務學習的加速效果（ Jaderbergetal.,2017)。類似地，作爲一種有助於狀態預測的方法，多預測的方法也被反覆 反復地提出過（見17.3節）。

另一個理解爲何學習輔助任務可以提升表現的簡單的方法是類比於經典條件反射這心理學現象（14.2節）。一種理解經典條件反射的方法是，進化使我們內建（非學習式的）了一個從特定信號的預測值到特定動作之間的反射關聯。例如，人和許多其他動物看起來有一種內建的眨眼反射機制 機製，當對於眼球將收到戳擊的預測值超過某個閾值的時候，就會閉眼。這個預測是學出來的，但是預測和閉眼之間的關聯是內建的，因此動物可以避免眼球受到突然的戳擊。類似地，恐懼和心率加快或者愣住之間的關聯、也可以是內建的，智慧體的設計者們可以做一些類似的事情，例如，自動駕駛汽車可以學習「向前開車不會導致碰撞」，然後將其「停車/避開」的行爲建立一個內建反射，當預測值超過一定閾值時觸發。或者考慮一個真空清潔機器人，其可以學習預測是否會在返回充電裝置前用盡電量，並且在該預測值變爲非零時，條件反射一樣地掉頭移動到充電站。準確的預測取決於房間的大小、機器人所在的房間、電池的年齡，機器人的設計者很難了解所有這些細節，讓設計者使用感測器的手段設計一個有效的演算法來決定是否回頭是很困難的，但是使學習到的預測則很容易做到這一點。我們預見到很多方法都會像這樣將學習到的預測和內建控制行爲的演算法有效結合在一起。
最後，也許輔助任務最重要的作用，是改進了我們本書之前所做的假設：即狀態的表不是固定的，而且智慧體知道這些表示。爲了解釋這個重要作用，我們首先要回過頭來了本書所做的假設的重要性以及去除它所帶來的影響。這將在17.3中介紹。

定義： 預測和控制不同種類的信號特徵

作用

17.2、基於選項理論的時序摘要

馬爾可夫決策過程形式上的一個吸引人的地方是，它可以有效地用在不同時間尺度的任務上。我們可以用它來形式化許多工，例如決定收縮哪一塊肌肉來抓取一個目標，乘坐哪一架航班方便地到達一個遙遠的城市，選擇哪一種工作來過上滿意的生活。這些任務在時間尺度上差異很大，然而每一個都可以表達成馬爾可夫決策過程（MDP),然後用本書中講述的規劃和學習過程完成。所有這些任務都涉及由與環境的相互作用、序貫決策以及一個隨時間累積的收益構成的目標，因此它們都可以被形式化成馬爾可夫決策過程。

儘管所有這些任務都可以被形式化爲MDP，但是我們可能認爲它們不能被形式化爲單一的MDP，因爲這些過程涉及的時間尺度都不同，例如選擇的種類和動作都截然不同。例如，把預定跨洲的航班和肌肉收縮放在同一時間尺度上是不合適的。但是對於其他任務而言，例如抓取、擲標槍、擊打棒球，用肌肉收縮的層次來刻畫可能剛剛好。人類可以無縫地在各個時間層次上切換，而沒有一點轉換的痕跡。那麼MDP框架可不可以被拉伸，從而同步地覆蓋所有這些時間層次呢？

人類可以無縫地在各個時間層次上切換，而沒有一點轉換的痕跡。那麼MDP框架可不可以被拉伸，從而同步地覆蓋所有這些時間層次呢？

也許是可以的，一種流行的觀點是：先形式化一個非常小的時間尺度上的MDP，從而許在更高的層次上使用擴充套件動作（毎個時刻對應於更低層次上的多個時刻）的規劃。爲了能到這一點，我們需要使用一個展開到多個時刻的「動作方針」的概念，井引人一個「終止」的概念。對這兩個概唸的通用的形式化方式是將它們用一個策略和一個狀態相關的終止函數γ來表達，就像在GVF中定義的那樣。我們將這樣的一個「策略終止函數」二元組定義爲一種廣義的動作，稱之爲「選項"。在t時刻執行一個選項 $ω=<π_ω，γ_ω>$ 就表示從 $π_ω(·|S_t)$ 中獲得一個動作$A_t$，然後在t+1時刻以$1-γ_ω(S_(t+1))$的概率終止。如果選項不在$t+1$時刻停止，那麼$A_(t+1)$從 $ π_ω(· |S_(t+1))$ 中選擇，而且選項在t+2時刻以$1-γ_ω(S_(t+2))$的概率終止。很容易就可以把低層次的動作看作選項的一種特例一每一個動作a都對應於一個選項（π_ω,γ_ω),這個選項的策略會選出一個動作（對於每個$s∈S,π_ω(s)=a$),並且其終止函數是零（對於個$s∈S+,γ_ω(s)=0$)。選項有效地擴充套件了動作空間。智慧體可以選擇一個低層次的動作/選項，在單步之後終止，或者選一個擴充套件的選項，它可能在執行多步之後才終止。

"選項」的架構設計允許它與低級別的動作進行角色互換。例如，一個動作價值函數的記號$q_π$可以被自然地推廣爲選項值函數，它以狀態和選項作爲輸人，仍然返回期望回報，只是產生這個期望回報的過程包括了從輸入狀態開始，執行輸人的選項直到它終止，並在之後繼續遵循策略π的整個過程。我們也可以把策略的概念推廣到層次化策略，它選擇的是選項而不是動作，其中每個選項被選中之後，都會一直執行到終止。在這些思想下，本書中的許多演算法都可以推廣到學習近似的選項值函數和層次化的策略。在最簡單的情況下，學到的策略從選項開始直接跳到選項結柬，更新只在選項結束的時候出現。更精細一些的做法是，更新可以在每一個時刻進行，使用一種「選項內部」的學習演算法，這通常需要離軌策略演算法。

選項的思想帶來的最重要的推廣也許是第3、4和8章中所提出的環境模型。關於「動作」的傳統模型是狀態轉移概率和採取這個動作的即時收益的期望。那麼傳統的動作模型如何推廣到選項模型呢？對於選項而言，合適的模型也應該包含有兩部分：一個部分對應於執行選項後產生的狀態轉移結果；另一個對應於執行選項過程中的累積收益的期望。選項模型的收益部分，類比於「狀態-動作」二元組的期望收益式（35),對於所有的
選項和所有的狀態s∈S，定義爲：

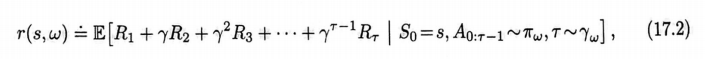
其中，τ是一個隨機時刻，代表選項的終止時刻，它由參數$γ_ω$決定。在這個等式中，需
要注意總體折扣係數 γ 所扮演的角色一一折扣是由γ決定的，但是選項的終止是由$γ_ω$
決定的。一個選項模型的狀態轉移部分則更爲精巧。這部分模型刻畫了每一個可能的選項結果狀態的概率（像在式3.4中一樣），但是在這裏，可能在多個時刻之後才能 纔能到達這個選項結果的狀態，其中的每個狀態都有不同程度的折扣。選項ω的這部分模型在如下公式中指定了ω的每個可能的起始狀態s，以及ω的每個可能的終止狀態$s`$

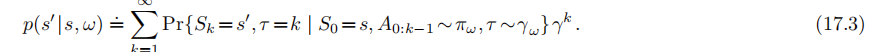
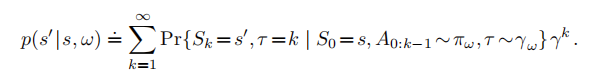
注意，由於存在折扣係數項$γ~k$，這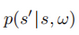裏的
不再是一個轉移概率，並且不再對於有可能的$s`$求和爲1(無論如何，我們會繼續在P中使用記號$|$）
上面關於選項模型的狀態轉移部分的定義使得我們可以爲所有的選項定義形式化的貝爾曼方程和動態規劃演算法，其中也包括作爲選項特例的低級別的動作。例如，對於層次化策略π來說，通用的貝爾曼方程是：

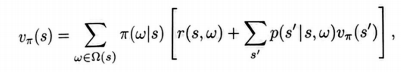
其中，$Ω_(s)$表示狀態s中所有可行的選項的集合。如果$Ω_(s)$僅僅包含低級別的動作，那這個方程退化爲通常的貝爾曼方程（式3.14),唯一不同的是γ被包含在新定義的p中，即式17.3,因此在此處沒有出現。類似地，相應的選項的規劃演算法中也沒有γ。例如，作爲式（4.10)的推廣，帶選項的價值送代演算法是：

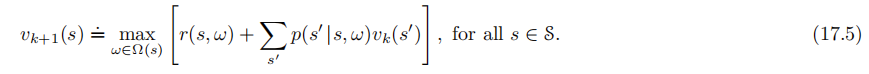
如果Ω(s）包含了每個狀態s下所有可行的低級別動作，那麼這個演算法會收斂到通常意義上的$v*$，從中我們可以計算出最優的策略。然而，如果我們能夠在每一個狀態下，只考慮所有可能選項Ω(s）的某個子集進行規劃，則可能更有用。這樣的話價值送代將會收斂到限制在給定的選項子集下的最優的層次化策略。儘管這個策略從全域性看可能是次優的，但收斂可能會更快，因爲我們只考慮較少的選項，而且每個選項都可以在時間上跳躍多步。

爲了在有選項的情況下做規劃，我們必須已知選項模型，或者學出選項模型。一個學出選項模型的自然方法是使用一系列的GVF（我們在上一節中定義過）來對它進行表示長後使用本書中提到的方法來學習GVF。對於選項模型的收益部分，不難看出如何做到這一點。我們僅僅需要把GVF的累計量選爲收益（Ct：=Rt),把它的策略設爲選項的策略（$π=π_ω$），把它的終止函數設爲折扣係數乘以選項的終止函數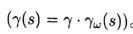
。如此一來，真實的GVF將等同於選項模型的收益部分，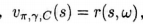
並且本書中介紹的各種學習方法都可以用來近似它。選項模型的狀態轉移部分會更復雜一些。我們需要對選項對應的每一個可能的終止狀態分配一個GVF。除了在選項終止且終止於相應的狀態時， 我們不希望這些GVF積累任何量。

這可以通過如下設定來實現：把預測轉移到s’的GVF的累計量寫爲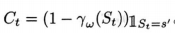
。該GVF的策略和終止函數都和選項模型的收益部分一樣設定。那麼真實的GVF就等同於選項的狀態轉移模型的s` 部分：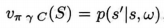
,這樣本書中介紹的方法也就可以用來學習它。儘管這其中的每一步看起來都很自然，但是把它們整合在一起（包括函數通近和其他關鍵部分）是很有挑戰性的，而且超出了現有最先進的技術水平。

練習17.1 在本節中展示了折扣情況下的選項，但是在使用函數通近的時候，折扣對於控制問題是否合適是有爭議的（參見10.4節）。那麼層次化策略的自然的貝爾曼方程形式應該是什麼樣的呢？它應當與式（17.4)中的類似，但需要在平均收益設定（10.3節）下進行定義。類比於式（172)和式（17.3),在平均收益設定下，選項模型的兩個部分分別是什麼樣子的呢？

17.3 觀測量和狀態

在本書中，我們都把學到的近似價值函數（還有第13章中的策略）寫成關於狀態的函數。這是本書的第工部分中介紹的方法的重大侷限，在這些方法中，學習得到的價值函數用一張表格來表示，因此任意的價值函數都能被精確近似。這種情況等同於假設環境的狀態完全可以被智慧體感知。但是在很多情況下，感測器輸入只會告訴你這個世界狀態的部分資訊。有些物件可能被其他的東西遮擋住了，或者在智慧體的身後，亦或是在幾裡之外。在這些情況下，關於環境的很重要的一部分資訊可能並不能直接觀察到。而且，把學習到的價值函數實現爲一個關於環境狀態空間的表格，是一種過強的、不現實而且侷限性很大的假設。

在本書第Ⅱ部分提出的參數化函數逼近框架則限制要少得多，甚至可以說它是沒有侷限性的（雖然這種說法是有爭議的）。在第Ⅱ部分中，我們保留了學習到的價值函數（和策略）是關於環境的狀態的函數這一假設，但是允許這些函數在參數化的框架下自由變化。
一個有些令人吃驚而且並不被廣泛認可的觀點是，函數逼近包含了「部分可觀測性」的很多方面。例如，如果有一個不可觀測的狀態變數，那麼我們通過選擇參數化的方式使得近似價值函數與這個變數無關。這樣做的效果就如同這個狀態變數是不可觀測的。正因爲如此，在所有參數化的情況下獲得的結果都可以被應用在部分可觀測的情況下，而不需要做任何改變。從這個意義上說，參數化函數逼近的情況包含了部分可觀測性的情況。

然而，如果不顯式地、明確地爲部分可觀測性建模，仍然有很多問題無法被深入研究，儘管我們在這裏不能給出一個完整的處理部分可觀測性的方法，但是我們可以大致列出需要做出的一些改變，以下是具體的四個步驟：
1、我們需要改變問題：環境所提供的不是其狀態的精確資訊，而僅僅是觀測量，一這是一個依賴於於狀態的變數，就像機器人的感測器那樣，提供關於狀態的部分資訊。與了簡化問題，我們假設收益是一個關於狀態的直接的、已知的函數（觀測量可能是一個，收益可能是它的某一個分量）。那麼環境互動將沒有明確的狀態或者收益，而僅僅出一個簡單的動作A_t∈A和觀測量O∈O的互動序列：5

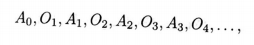
永遠這樣持續下去（與式3.1對比）或者形成「幕」，每幕都以一個特殊的終止觀測量來結束。

2、然後我們可以用觀測量和動作的序列來恢復本書中提到的狀態的概念。我們使用術語"歷史"以及記號Ht表示一個軌跡從初始部分一直到當前的觀測量：0。

歷史代表了我們在不看數據流外部資訊的情況下，對過去所能瞭解的最多資訊（因爲歷史是整個過去的數據流）。當然歷史會隨着t增長，從而變大而且笨重，狀態的想法就是歷史的某種「緊湊」的總結，對於預測未來而言，它和真實的歷史同等有用。我們看看這到底意味着什麼：爲了成爲歷史的總結，狀態必須是一個歷史的函數S=f(Ht),爲了能夠像歷史一樣對預測未來有用，它必須有我們所知道的馬爾可夫性。更正式的說法是，這是函數f的性質。對於所有的觀測量o∈O和動作a∈A，一個個函數f有馬爾可夫性，當且僅當任意被預測到同一個狀態（f(h)=f(h`))的兩個歷史h和h· 都對於它們的下一個觀測量有相同的概率。

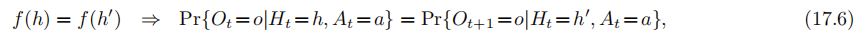
馬爾可夫狀態是預測下一個觀測量（式17.6)的良好基礎，但更重要的是，它是預測控制任何事情的良好基礎。例如，令一個測試序列爲任何特定的在未來可能發生的交替出現的「動作-觀測量」序列。比如一個三步的測試序列可以記爲：

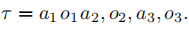
給定歷史h，這個測試序列的概率被定義爲：

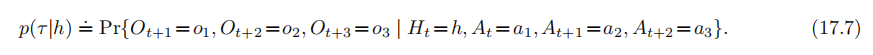
如果f是馬爾可夫的，而且h和h`是在f下會被對映到相同的狀態的兩個不同的歷史，那麼對於任意長度的任意測試序列$τ$，給定這兩個歷史時它們的概率一定是相同的：

換句話說，一個馬爾可夫狀態總結了對於預測測試序列的概率有用的所有歷史資訊。事實上，它總結了做任何預測所需要的全部資訊，包括預測任意的GVF以及最優的行爲（如果f是馬爾可夫的，那麼總會存在一個確定的函數π,使得選擇A：÷π(f(Ht)是最優的）。

將強化學習的概念擴充套件到部分可觀測的情況的第三步是需要考慮一些計算上的問題。
特別是，我們希望狀態是歷史的緊湊的總結。例如，對於一個馬爾可夫的函數f，對映到自己的函數完全滿足這個條件，然而並沒有什麼用，因爲正如我們之前所提到的，對應的S1=H1會隨着時間增長而變得笨重。但是更本質的原因是，這個歷史再也不會在未來出現了。智慧體永遠不會兩次進入同一個狀態（在一個持續性的任務中），因此永遠不會從表格型學習方法中獲益。我們希望我們的狀態是「緊湊」的，而且是馬爾可夫的。在如何獲得和更新狀態的問題上，我們也有類似的需求。我們並不真的想要一個包括「所有歷史」的函數f。相反地，出於計算上的考慮，我們偏向於通過相對簡單的增量式遞回計算獲得與f一樣的效果，這個計算過程使用下一個時刻的增量At 和 Ot+1 ：

其中，初始狀態S0是給定的。函數u又被稱作狀態更新函數。例如，如果f是對映到自身的函數（St=Ht),那麼u僅僅是在St 的後面加上了一個At和Ot+1.給定f，構造個相應的u總是可行的，但是可能在計算上並不方便，而且正如上面對映到自身的函數的例子，它可能不能產生一個「緊湊」的狀態。狀態更新函數在任何智慧體的架構中都是解決部分可觀測性問題的核心部分。它必須在計算上是高效的，因爲在看到狀態之前，我們不能採取任何動作或者做任何預測。

一個通過狀態更新函數獲得馬爾可夫狀態的典型例子採用了流行的貝葉斯方法，被
稱作「部分可觀測MDP"( Partially Observable MDP, POMDP)。在這個方法中，假定
存在一個完備定義的隱變數Xt,它真實反應環境的變化併產生可見的環境觀測量，但它們對於智慧體而言從來都是不可觀測的（不要將它與智慧體用於預測和決策的狀態S相混淆）。對於 POMDP而言，一種自然的馬爾可夫狀態S，就是給定歷史時在隱變數上的一個概率分佈，這個「概率分佈」被稱作置信狀態（ （belief state）。爲了更具體一些，假設在通常情況下，存在有限個隱變數:

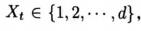
那麼置信狀態則是一個向量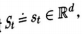

無論t如何增長，置信狀態都保持相同的大小（相同數量的成員）。假設我們有足夠多的關於環境內部如何工作的知識，它也可以由貝葉斯公式增量式地更新。特別地，置信狀態更新函數的第i個成員是

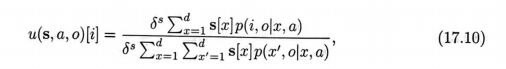
其中，a∈Ao∈O，置信狀態s∈Ra，其元素爲s。這裏有4個變數的p函數與MDP
中（滲見第3章）通常使用的並不一樣，而是在 POMDP情況下的基於隱狀態的推廣形
式：r,o이x,a)=Pr{X1=,O2=0IX1-1=a,A4-1=}。這個方法在理論研究中非常流
行、並且有非常重要的應用，但是其假設和計算複雜性的可延伸性太差，我們不推薦在人工智慧中使用該方法。

另ー個馬爾可夫狀態的例子是預測狀態表示（ Predictive State Representations,PSR).
PSR解決了 POMDP方法的弱點：在 POMDP中，智慧體的狀態S，的語意是以環境的隱狀態X爲基礎的。由於隱狀態無法被觀測，其學習也就比較困難。在PSR和相關方法中，智慧體狀態的語意是以未來的觀測量和動作的預測值爲基礎的，因而是可以觀測到的。在PSR中，一個馬爾可夫狀態被定義爲一個d維的概率向量，由d個「核心」測試序列的概率組成，測試序列則由前面介紹的式（17.7)所定義。這個向量之後由狀態更新函數u更新，它是貝葉斯公式的一種擴充套件，但以可觀測的數據爲基礎，這就讓它的學習變得更容易了。這個方法已經在很多方面得到了擴充套件，包括終端測試、組合測試、強有力的「譜」方法，還有從TD方法中學到的閉環和時序摘要測試。最好的理論進展有些是針對被稱爲可觀測的操作模型（ Observable Operator Models,OOM）和序列系統（Thom,2017）的。

在我們簡短的概要介紹中，處理強化學習中的部分可觀測性的第四步是重新引入近似的念。正如我們在第二部分中所討論的，想要達到人工智慧必須得接受近似方法。不僅於價值函數是這樣，對於狀態也是這樣。我們必須接受並且在「近似狀態」的概念下開展我們的工作。近似狀態將會在我們的演算法中扮演和原來一樣的角色，因此我們繼續對智款用的狀態使用記號S，儘管它可能不是馬爾可夫的。

也許近似狀態的最簡單的例子就是最近的觀測量S=O。當然這種方法不能夠處理變數資訊的情況。可能更好的表達方式是，對於某個k>1,使用最近的k個觀測量和動作來表達狀態：S：=On,A4-1O2-1…,Ar-k，這可以通過引入一個特殊的狀態更新函數來實現：每次加人新數據並平移，同時把最舊的數據刪除。k階歷史的方法仍然非常
簡單，但是相比於直接使用單個觀測量作爲狀態，它可以大大增加智慧體的能力。

當馬爾可夫性質（式17.6)只是被近似滿足的時候會發生什麼呢？不幸的是，當單步預測所定義的馬爾可夫性變得哪怕有一點不準 不準確的時候，長期預測的表現就可能會遭遇急劇的下滑。長期的測試序列、GVF，還有狀態更新函數都有可能近似得很糟糕。短期和長期的近似目標就是不一樣的。當前也沒有這個方面的有效的理論保證。

然而，仍然有理由認爲在本節中描述的通用思想可以用到近似的情況下。這個通用的思想就是：一個對於某些預測而言好的狀態，對其他的情況也會是好的（特別是，對於一個馬爾可夫狀態，如果它足夠做單步預測，則對其他的情況也是足夠的）。如果我們退步，不考慮馬爾可夫情況下的特定結果，則前面的通用思想與我們在17.1節中討論的多頭部學習和輔助任務是相似的。在17.1節，我們討論了對於輔助任務來說好的表示爲什麼對於主任務來說往往也是好的。這些思想合在一起就揭示了一個可以同時對部分可觀測性和表徵進行學習的方法：採用多重預測並以此來指導狀態特徵的構建。這樣一來，完美但並不可行的馬爾可夫性帶來的理論保證就被一個啓發式原則所替代，這個原則就是：對某些預測有益的資訊對於其他預測而言也會是好的。這種方法可以很好地與計算資源的規模相匹配。在大型電腦器上，人們可以嘗試大量的不同的預測：可能會傾向於那些接近於最感興趣的目標、最容易可靠地學習的預測。在這裏很重要的一點是，不要手動選擇預測目標，而智慧體應該做到這一點。而這可能需要一個通用的表達「預測」的語言，使得智慧體可以系統地試探一個廣大的可行預測的空間，從中發現最有用的內容。

特別地， POMDP和PSR方法都可以應用於近似狀態。狀態的語意在形成狀態更新
函數的時候非常有用，就像在這兩種方法和k階的方法中那樣。但對保持狀態內資訊的
有用性而言，語意正確的需求並沒有那麼強烈。有些狀態擴充的演算法，例如回聲狀態網
絡（ Jaeger,2002),幾乎保留了關於歷史的任何資訊，但是依然表現很好。這個領域依然
有很多的可能性，因此我們期待更多的工作和新的思想。針對近似狀態，學習狀態更新函數是強化學習中的表示學習問題的一個重要組成部分。

17.4 設計收益信號

強化學習相較於有監督學習的一個主要優勢是，強化學習並不依賴於細節性的監督資訊：生成一個收益信號並不依賴於「智慧體的哪個動作纔是正確的」這一先驗知識細節。

但是強化學習的成功應用很大程度上依賴於我們的收益信號在多大程度上符合了設計者制定的目標，以及這些信號能夠多好地衡量在達到目標過程中的進步。出於這些原因，設計收益信號是任何一個強化學習應用的重要部分。

設計收益信號指的是設計智慧體所在的環境的一個部分，這部分負責在t時刻產生一
個標量收益R送回到智慧體。在第14章末尾討論術語的時候，我們提到，稱B更像一個在動物大腦內部產生的信號，而不是在動物的外部環境中的一個物件或者事件。大腦中產生這些信號的部分已經進化了數百萬年，因此非常適應我們的祖先在將他們的基因傳遞下去的時候所面臨的各種挑戰。我們因此不應該認爲設計收益信號是一件容易的事情。

設計收益信號的一個挑戰來自於，智慧體需要學習，在行爲上接近並在最終達到設計者所希望的目標。如果設計者的目標很容易辨別，那麼這個任務可能很簡單，例如尋找個良好定義的問題的解，或者在一個良好定義的遊戲中取得高分。在這些例子中，我們通常可以通過「問題是否解決」和「遊戲分數是否提高」來定義收益函數。但是在有些問題中，目標並不容易被翻譯成收益函數，尤其是當這些問題需要智慧體做非常有技巧性的動作來完成複雜任務或者一系列任務的時候就更是如此，例如家務機器人助理所需要解決的問題。更進一步，強化學習智慧體可能會發現一些意想不到的方法使得環境可以給出收益信號，但其中有一些可能是我們並不想要的，甚至有時是很危險的方法。這對於任何像強化學習這樣依賴於優化的演算法而言，都是一個長期存在並且非常關鍵的挑戰。我們將在17.6節，也就是本書的最後一節中詳細討論這個問題。

即使有一個簡單且易於辨識的目標，收益稀的問題仍然時常出現。足夠緊地提供非零收益讓智慧體實現一次目標，本身就已經是一個今人畏懼的挑戰，更不要說讓它高效地從各種各樣的初始狀態下進行學習了。那些可以明確地觸發收益的「狀態動作」二元組可能很少，而且相互之間隔得很遠：且代表着向目標前進的收益也可能並不常見，因爲朝
向目標的進步總是很難甚至是無法衡量的。智慧體可能會長期沒有目的地漫遊（ Minsky
1961所稱的「高原問題」）。

在實踐中，設計收益信號通常會歸到一個反覆 反復試驗的搜尋過程，直到找到一個可以產生合理結果的信號。如果智慧體沒有成功學習，學得太慢，或者學習到了錯誤的東西，那麼這個應用的設計者會調整收益信號並且再試一次。爲了做到這一點，設計者會對智慧體的表現用某種評估標準來衡量，而他會把這種評估標準翻譯成一個收益信號，使得智慧體的目標和設計者自己的目標相匹配。如果學習的進程大慢了，那麼設計者可能會嘗試設計個非稀硫的信號，其可以在智慧體與環境互動的過程中更有效地指導學習。解決稀硫收益問題的一個非常誘人的手段是，以設計者認爲達到最終目標所經歷的重要的幾個階段作爲子目標，對這些子目標提供收益函數。但是，當使用這些有明確目的性的補充收益來擴充原來的收益函數時，也可能會使智慧體的行爲與我們的預期大相徑庭智慧體可能最終根本不會達到總的目標。一個更好的提供這樣的指導的方法是，把收益函數放在一邊而對價值函數的逼近過程進行擴充，給它擴充一個描述最終目標的初始猜測，或描述部分目標的初始猜測。例如，假設我們想把：S→R作爲真實的最優價值函數
U。的一個初始猜測，並且我們使用關於特徵x:S→Rd的線性函數逼近，那麼我們可以
把初始的價值函數逼近形式定義爲：

然後按照慣例更新權重w，如果初始的權重向量是0,那麼初始的價值函數則是t,
但是漸近解的品質會像往常一樣由特徵向量決定。可以針對任意的非線性函數通近器和任
意形式的u來做這種初始化，儘管這並不保證能加速學習。

一個處理稀疏收益問題的非常有效的方式是塑造技術，它由心理學家B.F. Skinne
提出，並在本書的14.3節中有所介紹。這種技術的有效性依賴於一個事實：稀疏收益問題並不只是收益信號本身的問題，它們也是智慧體策略的問題，有些策略會阻礙智慧體頻繁達到可以產生收益的狀態。塑造技術會在學習過程中不斷改變收益信號：給定智慧體的初始行爲，從一個不那麼稀疏的收益信號開始，漸漸地把它調整到適合最初感興趣的問題的收益信號。智慧體面臨一系列難度逐漸増加的強化學習問題，其中在每個階段學習到的東西，可以讓下一個更難的問題變得相對簡單一些。這是因爲智慧體通過學習簡單問題得到了先驗知識，這些知識使得它能夠更加頻繁地獲得複雜問題下的收益；而如果不學習先驗知識就直接優化複雜問題的收益，則收益會非常稀疏。「塑造」是訓練動物過程中的個基礎技術，它在計算強化學習中非常有效。

如果我們對於收益信號如何設計一籌莫展，但是有另外一個智慧體，它可能是一個人類，已經是該領域的專家，並且它的行爲可以被我們觀察到，那麼我們可以如何利用這點呢？在這種情況下，我們可以使用被稱爲「模仿學習」「從示範中學習」和「學徒學習」的演算法。這裏的思想是從專家智慧體中獲得收益，同時保留進一步提升的可能性。從專家的行爲中學習可以通過直接的有監督學習，或者通過被稱作「逆強化學習」的技術抽取收
益函數，然後使用強化學習演算法從這個收益函數學出一個策略。Ng和Rusl(200研
究了逆強化學習的任務，他們嘗試僅僅從專家的行爲中恢復出專家的收益信號。但這種做法無法找到精確解，因爲一個策略可能對很多個不同的收益信號而言都是最優的（例如，任何對所有狀態和動作給予相同收益的信號）。但是，我們仍然可能找到合理的候選收益信號。只不過這個過程需要很強的假設，包括對環境動態特性的先驗知識，以及與收益信號成線性關係的特徵向量。同時，這個方法也要求對問題做多次完全求解（例如通過動態
規劃）。雖然有這些困難，但是 Abbeel 7和Ng(2004)稱逆強化學習有時會比有監督學習更
有效
另一個找到好的收益信號的方法，是將試錯搜尋過程自動化以找到好的信號。從應用角度來說，收益信號是學習演算法的一個參數。正如我們可以對演算法的其他參數所做的那樣，我們可以自定義可行的搜尋空間，然後用優化演算法自動優化這些收益信號。優化演算法是這樣評估每一個候選收益信號的：以該收益信號執行強化學習演算法若幹步，然後用一個包含設計者真實目標的「高階」目標函數來計算評分，不需要考慮該智慧體的侷限。甚至
可以通過線上梯度上升來提升收益信號，其中梯度來自於高階的目標函數（Sorg、 Lewis和 Singh,2010)。把這個演算法與真實世界相聯繫的話，優化高階目標函數可以類比爲進
化，其中高階優化函數代表動物的進化適應程度，這通過能活到繁殖年齡的後代數量來衡量。

這種具有上下兩層優化演算法（一層類似於進化，另一層是智慧體個體的強化學習）
的計算實驗已經證實，直覺本身並不總足以用來設計一個好的收益信號（ Singh、 Lewis和 Barto,200)。利用高階目標函數所衡量的強化學習智慧體的效能表現，可能會對智慧
體收益信號的某些細節方面特別敏感，這些敏感性來源於智慧體本身的侷限以及它在其活動和學習的環境。這些實驗也表明一個智慧體的目標不應該總是與智慧體設計者的目標一致。

最初這件事情顯得很反直覺，但是對於一個智慧體而言，它不可能不管收益信號是麼就達到設計者的目標。智慧體需要在很多限制下學習，例如有限的計算能耗、有限的環境資訊或者有限的學習時間。當有這樣那樣的限制的時候，學習去達成一個與設計者目標
不同的目標，而不是直接去追求設計者的目標（Sorg、 Singh和Lewi,2010:Sorg,201)
這可能有時會更加接近於設計者的初衷。在自然界中很容易找到這樣的例子，因爲我們不能直接接觸到大多數食物的營養值，我們的收益信號的設計者一一進化一一給予我們
一個收益信號讓我們去找某些特定味道。儘管這當然並不絕對可靠（事實上，在某些與祖先環境不同的環境中可能是有害的），但這個信號補償了我們之前許多的限制：有限的感官功能，有限的學習時間，以及在尋找健康飲食的過程中進行個體嘗試實驗所冒的風險。類似地，因爲動物並不能實際觀察到它的進化適應性，所以進化適應性的目標函數本身並不能作爲收益信號。相反，進化過程所提供的一系列收益信號都是可以觀測的，並且是對進化適應性敏感的。

最我們要記住，強化學習智慧體並不一定是一個完整的有機物或者機器人。它可能是一個更大的行爲系統的一部分。這意味着收益信號可能被更大的行動智慧體內部的事情所影響，例如動機、記憶、想法甚至幻覺。收益信號可能也依賴於學習過程本身的一些性質，比如衡量學習中進步了多少。讓收益信號對這樣的內部資訊敏感，可以使智慧體作爲「認知架構」的一部分，學習如何控制認知架構，同時也可以獲取一些特定的知識和技能。這些技能很難只依賴於外部的收益信號學習到。這種可能性導致了「內在激勵的強化學習」這個思想，稍後我們會簡要地討論這個問題。

5 遺留問題

在本書中，我們介紹了通向人工智慧的強化學習方法的基礎知識。粗略地說，這個方
法依賴於模型無關和模型相關的方法的結合（如第8章中的Dyma框架所示），並利用第Ⅱ
部分中介紹的函數通近技術。其中的關注焦點是「線上」和「增量式」的演算法（我們甚至認爲這些方法比基於模型的方法更爲基本），以及如何在離軌策略訓練的情形中使用這些演算法。後者的完整應用只在這最後一章中有所闡述。也就是說，我們之前一直將離軌策略學習視爲解決試探和開發之間矛盾的一種吸引人的方式，但是隻有在這一章中，我們才真正完整地討論了依賴於離軌策略學習的應用，包括學習GVF的同時也學習多個不同的輔助任務，還有通過時序摘要的選項模型來對世界進行層次化的學習。正如我們不斷在本書中指出的，並且本章中所討論的未來潛在研究方向也表明，目前仍有很多工作有待完成。但是，假設我們認可本書中全部的內容以及本章到現在爲止所概括的全部方向，那麼還剩下的是什麼呢？當然我們不能確切地知道什麼是需要的，但是我們可以做一些猜測。在這
・節中我們強調6個更長遠的問題，有待未來的研究去解決。

第一個問題是，我們仍然需要更強大的參數化函數逼近方法，它應當可以在完全增量式和線上式的設定下很好地工作。基於深度學習和人工神經網路的方法是這個方向上的重要一步，但是它們仍然只是在極大的數據集上批次訓練才能 纔能得到很好的效果，要麼是大量離線地自我對局博弈，要麼是通過多個智慧體在同一個任務上交錯地採集經驗來學習。這些以及其他的一些設定都是爲了解決當下的深度學習方法的侷限，即深度學習方法在增量式、線上式學習的設定下會陷人掙扎，而增量式和線上式學習又恰恰是本書中強調的最自然的強化學習方法的特質。這個問題又被稱作「災難性的幹找」，或者「相關的數據」。每當學習到一些新的東西時，它都傾向於忘記之前學的東西，而不是將新知識作爲補充，這會導致之前學習到的那些優點都丟失。例如「回放快取」之類的技術經常被用於儲存和重新導出舊的數據，使得之前學到的優點不至於永久丟失。我們必須誠實地說，目前的深度學習方法並不完全適合線上學習。我們找不到這種限制無法解決的理由，但是迄今爲止，在保持深度學習優勢的同時解決這個問題的演算法仍然還沒有被設計出來。大部分當下的深度學習研究的導向是在這個限制下工作而不是去掉這個限制。

第二點（也許是緊密相連的），我們仍然需要一些方法來學習特徵表示，使得後續的學習能夠很好地推廣。這個題是一個更廣義的問題（被稱爲「表徵學習」「構造型歸納」和「元學習」）的例子。我們如何使用經驗去學習歸納各種偏差，使得未來的學習能夠得到更好的推廣也因此學得更快，而不只是學習一個想要的函數。這是一個很老的問題，可以道潮到20世紀50年代和60年代的人工智慧和模式識別的起源。這樣的年代可能會止人感到猶豫，也許這個問題沒有好的解決方案。但是同樣也有可能是我們尚未到達找出解決方案並展示它的有效性的階段。如今的機器學習是在一個遠大於過去的規模上進行的。一個好的表徵學習方法可能帶來的收益越來越清晰。我們注意到，在一個新的機器學
習年會一一國際表徵學習會議（ International Conference on Learning Representations
ICLR）上，自2013年起每年都有人採討這個問題。但在強化學習的語境下探索表徵學習則不是那麼常見。強化學習給這個舊間題帶來了許多新的可能性，例如17.1節中提到的軸助任務。在強化學習中，表徵學習的問題與173節中討論的學習狀態更新函數的問題是一致的。

第三點，我們仍然需要使用可延伸的方法在學習到的環境模型中進行規劃。規劃方
法已經被證明在某些應用上極爲有效，如 Alphago Zero和計算機國際象棋等，這些問題
中的環境模型可以從遊戲的規則或者人類設計者的知識中完整地得到。但是在完全基於模型的強化學習任務中，需要從數據中學習環境模型，然後再用於規劃，可很少有成功的例
子。第8章中介紹的Dyna系統是一個例子，但是正如我們當時所討論並且也在大部分
隨後的工作中被人提及的，它使用了一個不帶函數通近的表格型模型，這在很大程度上限了它的應用範國。只有少部分的研究探討了線性模型的使用、更少的研究同時了在172節中討論的基於選項的時序摘要方法。

爲了使規劃方法可以在學習得到的環境模型上有效地使用，我們還需要做很多工作。例如，模型的學習過程應該是選擇式的，因爲模型的範國會嚴重影響規劃的效率。如果一個模型注重於最重要的選項的關鍵結果，則規劃可能是快速和高效的；但是如果一個模型包含了不太可能被選到的選項的非主要後果的詳細資訊，則規劃可能幾乎沒有什麼用。環境模型應該以優化規劃過程爲目標，謹值而明智地構建其狀態和動態特性。應該持續地監測模型的各個方面，以瞭解它們對規劃效率貢獻或者減損的程度。本領域尚未解決這個複雜的問題或者設計出考慮其影響的模型學習演算法。

第四個在未來的研究中需要重點解決的問題，是自動化智慧體的任務選擇過程，智慧體在這些任務上工作並且使用這些任務提升自己的競爭力。在機器學習中，人類設計者爲智慧體設計學習的目標是一件很常見的事情。因爲這些任務是提前已知而且固定的，因此它們可以被內嵌在學習演算法的程式碼中。然而如果我們看得更遠一些，則我們可能希望智慧體對於將來想掌握什麼技能做出自己的選擇。這可能是某個特定的已知的大任務中的一個子任務，或者它們可能意圖創造一些積木式的模組，允許智慧體在一些尚未見過但是將來可能面臨的問題上更加高效地學習。

這些任務可能像17.1節中討論的輔助任務或者GVF，或者是用17.2節中討論的基於選項的方法解決的任務。例如在構建一個GVF的過程中，累積量、策略、終止函數分別應該是什麼樣子的？當前的最優方法是手動選擇它們，但是如果我們可以把這些任務選擇變得自動化，那麼它可能會更強大並且推廣性也更強，尤其是當任務選擇來自於智慧體已經構建的一些「積木」的時候就更是如此，這些「積木」可能是之前在表徵學習或者在子問題的經驗學習中產生的結果。如果GVF的設計是自動化的，那麼設計的選擇本身將會被顯式地表達出來：它們將會在計算機中以一種可以設定、改變、操控、篩選和搜尋的方式自動組織起來，而不是在設計者的大腦中，隨後寫進程式碼裡。之後任務可以一個接着
一個地被層次化組織起來，就像人工神經網路中的特徵一樣。任務就是一個一個的問題，而人工神經網路的內容就是這些問題的答案。我們期望將來有一個完整的層次化的問題與現代深度學習方法提供的層次化的答案相匹配。

第五個我們認爲對未來研究至關重要的問題是，通過實現某種可計算的好奇心來推動行爲和學習之間的相互作用。在本章中我們想象過一個場景：從一個經驗流中，通過離軌策略的方法，同時學習多個任務。採取的動作當然會影響經驗流，而經驗流反過來也會決定學習會出現多少次，什麼任務將會被學習。當收益信號不可用，或者不被智慧體行爲強烈影響的時候，智慧體可以自由選擇動作，在某種意義上最佳化這些任務上的學習，也就是說使用某些衡量學習進度的指標作爲內在的收益，來實現一種「好奇心」的計算形式。除了衡量學習進度之外，內在的收益函數可以以其他的可能性，找到最出人意料、新奇或者有趣的輸人，或者評價智慧體對環境造成影響的能力。用這些方式產生的內在收益信號，可以被智慧體用來給自己提出任務，任務的提出可以通過定義輔助任務、GVF或者選項等方式實現，以使得學到的技能可以提升智慧體掌握未來任務的能力。從結果上看，這很像計算意義上的玩要。現在已經有了很多關於使用內在收益信號的研究，在這個大的方向上還有很多激動人心的話題，等待未來的研究去揭示。

最後一個在將來的研究中需要注意的問題是開發足夠安全（達到可以接受的程度）的方法將強化學習智慧體嵌入真實物理環境中，從而保證強化學習帶來的好處超過其帶來的危害。這是未來研究最重要的一個方向之一，我們將在下一節中討論它。

6、

我們在20世紀90年代中期撰寫本書第1版的時候，人工智慧取得了顯著的進展，而且產生了一定的社會效應，儘管這個時期大多數激動人心的進展只是品示出人工智慧可能的前景而已。機器學習就是這個前景中的一部分，但是對於人工智慧而言還不能算是不可或缺的。如今人工智慧的前景已經落地爲應用，而且正在改變百萬人的生活。機器學習本身也成爲了一項關鍵技術。在我們寫本書第2版的時候，一些人工智慧方面最卓越的成就已經包括了強化學習技術，比如著名的「深度強化學習」一一強化學習與深度人工神經網路結合。我們正處在一波人工智慧真實場景應用的浪潮之中，它們中將會有很多都使用深度或者非深度的強化學習，我們很難預料它們將以什麼樣的方式影響我們的生活。

但是大量真實世界中的成功案例並不代表真正的人工智慧已經實現了。儘管人工智在很多領域都取得了很大的進展，但是人工智慧與人類智慧，甚至與動物智慧之間的鴻海都是很大的。人工智慧在某些領域能有超過人類的表現，甚至是圍棋這種非常難的遊戲然而開發像人類這樣完整地擁有通用適應性和解決問題的能力、複雜的情感系統和創造力，以及從經驗中快速學習的能力的可互動式的智慧體仍然任重道遠。強化學習作爲一關注於動態環境互動式學習的技術，在將來會發展爲這種智慧體的不可或缺的部分。強化學習與心理學及神經科學的聯繫（第14和15章）弱化了其與人工智慧其他的出期目標之間的關聯，即掲示關於心智的一些關鍵問題，以及心智如何從大腦中產生。強化學習已經幫助我們理解了大腦的收益機制 機製、動機和做決策的過程。因此有理由相信，在計算精神疾病學相結合之後，強化學習將會幫助我們研發治療精神親亂，包括藥物濫用和藥物成的方法。

強化學習在未來將會取得的另一個成就是輔助人類決策。在模擬模擬環境中進行強化學習，從中得到的決策函數可以指導人類做決策，比如教育、醫療、交通、能源、公共部門的資源排程。與其密切相關的一個強化學習的特徵是，它總是考慮決策的長期效應。這在圍棋和西洋雙陸棋中是非常明顯的，這些也正是強化學習給人留下最深刻印象的案例同時這也是收關我們人類和星球命運的諸多高風險決策的特徵。在過去的很多領域中策分析人員已經使用了強化學習，並將其決策用於指導人類。使用高階的函數通近方法和大量的計算資源，強化學習方法已經展現出了一些潛力，期望攻克將傳統決策輔助方法推廣到更大規模、更復雜問題的難題。
人工智慧的快速發展讓我們開始擔心它可能對社會甚至人類本身造成嚴重的威脅。著
名的科學家和人工智慧先驅 Herbert Simon早在2000年（ Simon,2000手CMIU舉辦的地球研討會（ Earthware Symposium）上的一個演講中，就預言了這一點。他指出在任何
新形式的知識中，前景和危險都存在着永恆的衝突。他用古希臘神話中普羅米修斯和潘多拉之盒的例子打比方，現代科學的英雄普羅米修斯，爲了人類的福社，從諸神那裏盜取火
種；而開啓潘多拉之盒，只是一個小小的無意之舉，卻給人類帶來了災難。 Simon認爲我
們需要承認這樣的衝突是不可避免的，同時應該把自己當作未來的設計者而不是觀衆，我們更傾向於做普羅米修斯那樣的決策。這對於強化學習來說非常正確，如果不就地部署強化學習，它在給社會帶來福利的同時，也有可能造成我們不希望看到的後果。因此，包括強化學習在內的人工智慧應用，其安全性是一個需要重視的課題。

一個強化學習智慧體可以通過與真實世界環境、模擬環境（模擬真實世界的一部分）或者這兩者的結合環境進行互動而學習。模擬器提供安全的環境，以供智慧體自由試探，而不需要考慮對自己/環境帶來的危害。在大多數現有的應用中，決策是通過與模擬環境互動，而不是直接與真實世界互動學習到的。除了避免在真實世界中造成不希望看到的後果之外，在模擬環境中學習，可以得到模擬的無窮無盡的數據，這比在真實環境中得到這些數據要容易得多。而且由於在模擬環境下，因此互動的速度通常比在真實環境中快，般在模擬環境中的學習也要快於在真實世界環境中的學習。

一個強化學習智慧體可以通過與真實世界環境、模擬環境（模擬真實世界的一部分）或者這兩者的結合環境進行互動而學習。模擬器提供安全的環境，以供智慧體自由試探，而不需要考慮對自己/環境帶來的危害。在大多數現有的應用中，決策是通過與模擬環境互動，而不是直接與真實世界互動學習到的。除了避免在真實世界中造成不希望看到的後果之外，在模擬環境中學習，可以得到模擬的無窮無盡的數據，這比在真實環境中得到這些數據要容易得多。而且由於在模擬環境下，因此互動的速度通常比在真實環境中快，般在模擬環境中的學習也要快於在真實世界環境中的學習。

然而，展現強化學習的全部潛力需要將智慧體置於真實世界的經驗流中，在我們的真實世界中行動、試探、學習，而不是僅僅在它們的虛擬世界中。總而言之，強化學習演算法（至少在本書中關注的那些）被設計成線上式的，並且它們在很多方面都在效仿動物如何在不穩定和有敵人的環境下存活。嵌入真實世界中的強化學習智慧體可以在實現人工智慧放大、擴充人類能力的過程中起到變革性的作用。

希望我們的強化學習智慧體在真實環境中學習的一個主要原因是：以極高的保真度模擬真實世界的經驗通常是很困難甚至是不可能的，因而很難保證在模擬世界學習到的策略，無論是通過強化學習還是其他別的方法學到的，其可以安全並良好地指導真實的動作。這對於某些依賴於人類行爲的動態環境而言尤其明顯，例如，教育、醫療、交通、公共政策，在這些環境中，提升決策力可以帶來切實的收益。然而部署這些智慧體到真實世界中，需要考慮人工智慧可能造成的危險。
其中有些危險是與強化學習密切相關的。因爲強化學習依賴於優化，因此它繼承所有優化方法的優點和缺點。其中一個缺點是設計目標函數的問題，在強化學習中這被稱作收益信號，它幫助智慧體學到我們想要的行爲，同時規避那些我們不想要的行爲。我們在17.4節中提到，強化學習智慧體可能會試探到意想不到的方式，通過這種方式使它們的環境傳遞收益，而有些方式並不是我們想要的，甚至是危險的。當我們只是非直接地制定我們想要系統學習的東西時，正如我們設計強化學習的收益信號那樣，在學習結東之前，我們不會知道我們的智慧體距離完成我們的期望有多近。這並不是強化學習所帶來的新問題，在文學和工程實踐中這個問題的提出已經很久了，例如在歌德的詩歌
「魔法師的學徒」（ Goethe1878)中，學徒對掃帚施法，以幫助他取水，但結果卻造成了出人意料的洪水，這是因爲學徒對魔法的掌握不到家。在工程中， Norbert Wiener，控制論（ cybernetics）的莫基人，早在半個世紀以前就指出了這個題。他把這個問題聯繫到了一個超自然的故事「猴子的爪子」（ Wiener,19640):「它滿足了你向他要的，但並不是你應該向他要的，或者不是你本來的意圖。」這個問題也在現代的文獻中有長篇討論（Nd
Bostrom2014)。任何在強化學習方面有經驗的人都可能發現他們的系統找到了一些出人
意料的方式來提高收益。有些時候意想不到的行爲是很好的，它以一種全新的方式解決了問題。但是在其他情況下，智慧體學習到的東西違背了系統設計者的初衷，因爲設計者完全沒有考慮到某些情況。仔細設計收益函數是非常重要的，它幫助智慧體在真實世界中行動，且不會給人類以觀察其行爲和動機並輕易幹擾它的行爲的機會。

儘管優化可能帶來非預期的負面效果，但數百年來，優化一直在被工程師、架構師還有潛在的可能造福人類的設計者們廣泛使用。我們生活中很多好的方面都依賴於優化演算法的應用。另一方面，也有很多方法被提出來解決優化潛在的風險，例如增加硬或軟的約束，使用魯棒和風險低的策略來限制優化，使用多目標函數優化等。這些方法中有些已經用到了強化學習中，而且更多這方面的研究還有待進行。如何把強化學習智慧體的目標調整成我們人類的目標，仍然是個難題。

另一個強化學習在真實世界中行動和學習帶來的挑戰是，我們不僅僅關注智慧體學習的最終效果，而且關注其在學習時的行爲方式。如何保證智慧體可以得到足夠多的經驗以學習一個高效能的決策，同時又能保證不損害環境、其他智慧體或者它本身（更現實地說如何把傷害的可能性降得儘可能低）？這個問題並不新鮮，也不只在強化學習中存在。對於嵌入式強化學習，風險控制和減輕問題與控制工程師們在最初使用自動化控制時所面臨的同題是一樣的。那時控制器的行爲並不可控，很多時候還可能有災難性後果，例如對飛機和精密化學過程的控制。控制的應用依賴於精細的系統建模、模型驗證和大量的測試。關於讓事先完全不瞭解的動態系統保證收斂和適配控制器的穩定性，已經有大量的理論。理論的保證從來不是萬能的，因爲它們依賴於數學上的假設成立。但是如果沒有這些理論與風險控制和減輕的實踐相結合，自適應或者其他型別的自動控制就不會像今天我們看到的那樣，可以有效地提升品質、效率和成本收益。未來強化學習研究最重要的方向之一是適應和改善現有方法，以控制嵌入式的智慧體在可接受的程度上足夠安全地在真實物理環境中工作。
在最後，我們回到 Simon的號召：我們要意識到我們是未來的設計者，而不僅僅是
觀衆。通過我們作爲個體所做的決策，以及我們對於社會如何治理所施加的影響，我們可以共同努力以保證新科技帶來的好處大於其帶來的危害。在強化學習領域裏有充足的機會來做這件事情，因爲它既可以幫助提升這個星球上生命的品質，促進公平和可持續發展也有可能帶來新的危機。現在已經存在的一個威脅就是人工智慧應用造成了許多人的失業。當然我們也有充分的理由去相信，人工智慧帶來的好處將遠大於其造成的危害。關於安全問題，強化學習帶來的危害並沒有和當下已經被廣泛採用的相關領域的控制優化演算法帶來的危害有本質的區別。強化學習未來的應用涉足真實世界時，開發者們有義務遵循同類技術中成熟的實踐經驗，同時拓展它們，以保證普羅米修斯一直佔據上風。

參考文獻 歷史評註

17.1廣義的價值函數最早是 Sutton和他的同事（ Sutton,195a; Sutton et al,201; Modayil、
White和Sutn,2013)提出的。Ring提出了（正在準備中）一種使用GVF（「預報」）的
延伸思想實驗，已經有一定的影響力，不過尚未發表。
使用多個頭部的強化學習是由 Jaderberg et al.(2017)首次展示的， Bellemare、 Dabney和 Munos(2017)等人證實了預測收益分佈的更多資訊可以顯著提升學習速度來實現對其期望
的優化（這也是輔助任務的一個例子）。在這之後，很多研究者都開始在這個方向開展研究工作
就我們所知，經典條件反射作爲學習預測的一般理論以及對預測的內在反射性反應並沒有在
心理學的文獻中得到過明確闡述。 Modayil和Sutn(2014)將其描述爲一種控制機器人和其
他智慧體的方法，稱爲「巴甫洛夫控制」，暗示其根源爲條件反射。

172將動作的時序摘要過程形式化爲「選項」的過程是 Sutton、 Precup和 Singh(199等人提出
的，這也基於前人的工作，包括Par(199和Sutt(1995a）以及半MIDP的經典工作（例如，見 Puterman,1994). Precup(200的博士論文完整地提出了選項的思想。這些早期工
作一個很大的侷限是它們沒有處理離軌策略情況下的函數逼近。選項內部的學習通常來說需要離軌策略方法，那時還不能通過函數通近來可靠地完成。儘管現在我們有了一系列使用函數通近的穩定離軌策略演算法，但它們與選項的結合並沒有在本書出版的時候被真正地發掘出
來。 Barto和 Mahadevan(200還有 Hengst(2012)回顧了形式化的選項，還有其他的時序
摘要演算法。
使用GVF實現帶選項的模型在前文中沒有提到。我們的介紹中使用了 Modayil、 White和 Sutton(2014)等人提出的技巧，在策略結束的時候預測信號。
第17章前沿技術
使用函數通近來學習帶選項的模型的部分工作由 Bacon、Harb和 Precup(2017)等人提出。
目前的文獻中還沒有人提出把選項和帶選項的模型拓展到平均收益的情形。
173 Monahan(1982)給出了一個關於 POMDP方法的很好的展示。PSR和測試序列的概念由 Littman、 Sutton和 Singh(2002)等人提出。OOM由 Jaeger(1997,1908,2000提出。統一PSR、OOM和很多其他工作的序列系統，由 Michael Thon(2017;Thon和3 Beger
2015)在博土論文中提出。
強化學習與非馬爾可夫狀態表示的理論由 Singh、 Jaakkola和 Jordan(194; Jaakkola, Singh和 Jordan,1995)明確提出，早期的處理部分可觀測性的強化學習方法由 Chrisman(192)
Mccallum(1993, 1995). Parr i Russell(1995). Littman Cassandra M Kaelbling(1995)
還有 by Lin和 Mitchell(1992)提出
17.4早期關於強化學習的建議和教學參考包括Lin(1992), Maclin和 Shavlik(199), Clouse(1996),還有 Clouse和 Utgoff(192)
不應該將 Skinner的塑造技術與Ng、 Harada和Rusl(190提出的"基於的造」技術相混酒。 Wiewiora(2003)說明了該技術實際上與一個更簡單的思想等價：給價值函數提供
初始近似，如式（17.11)所示。

17.5我們推薦由 Goodfellow、 Bengio和 Courville(20160)所著的討論當下深度學習技術的書ANN中的災難性幹找問題由 Mccloskey和 Cohen(1989), Ratcliff(1990),還有 French(1999提出。回放快取的技術由1in(1992)提出，其著名應用是Atan遊戲系統（165節
Mnih et al.,2013,2015).
Minsky(1961)是第一個認識到表徵學習問題的人。
爲數不多的使用學習到的近似模型做規劃的研究由 Kuvayev和 Sutton(1996), Sutton
Szepesvari、 Geramifard和 Bowling(2008), Nouri和 Littman(2009),還有 Hester和 Stone
（2012)等人做
在人工智慧中，模型的設計需要仔細選擇以避免過慢的規劃，這是人們熟知的。一些經典的工
作包括 Minton(1990和 Tambe、 Newell,還有 Rosenbloom(199 Hauskrecht、 Meulear
Kaelbling、Dean和 Boutilier(1998)在帶確定性的選項的MDP中展示了相應的效果
Schmidhuber(1991a,b）指出，如果收益信號是關於智慧體的環境改普得有多快的一個函數那麼像好奇心那樣的事情會導致怎樣的後果。由 Klyubin、 Polan和 Nehaniv(200提出的
授權函數是一個資訊理論的度量，衡量智慧體控制環境的能力，它也可以作爲一種內在的收益
信號。 Baldassarre和 Mirolli(2013)的文章研究生物學和計算角度上的內在收益和動機，包括一種「內在激勵的強化學習」的觀點，使用了由 Singh、 Barto和 Chentenez(2004)提出的術語。同時可以參考 Oudeyer和 Kaplan(2007), Oudeyer、 Kaplan和 Hafner(200),還有 Barto(2013)的工作。