指令碼語言編譯前端演算法筆記
一、NFA和DFA:正則表達式處理
1. 在詞法分析階段,可以手工構造有限自動機(FSA,或 FSM)實現詞法解析,過程比較簡單。現在不需要再手工構造詞法分析器,而是直接用正則表達式解析詞法:
(1)首先,把正則表達式翻譯成非確定的有限自動機(Nondeterministic Finite Automaton,NFA)。
(2)其次,基於NFA處理字串,看看它有什麼特點。
(3)然後,把非確定的有限自動機轉換成確定的有限自動機(Deterministic Finite Automaton,DFA)。
(4)最後,執行DFA,看看它有什麼特點。
在詞法分析階段,有限自動機(FSA)有有限個狀態,識別Token的過程就是FSA狀態遷移的過程。其中,FSA分爲確定的有限自動機(DFA)和非確定的有限自動機(NFA)。DFA的特點是在任何一個狀態,基於輸入的字串都能做一個確定的轉換,比如:

而NFA的特點是,它存在某些狀態,針對某些輸入不能做一個確定的轉換,這又細分成兩種情況:
(1)對於一個輸入,它有兩個狀態可以轉換。
(2)存在某種轉換,在沒有任何輸入的情況下,也可以從一個狀態遷移到另一個狀態。
比如,「a[a-zA-Z0-9]*bc」這個正則表達式對字串的要求是以a開頭,以bc結尾,a和bc之間可以有任意多個字母或數位。在下圖中狀態1的節點輸入b時,這個狀態是有兩條路徑可以選擇的,所以這個有限自動機是一個NFA:
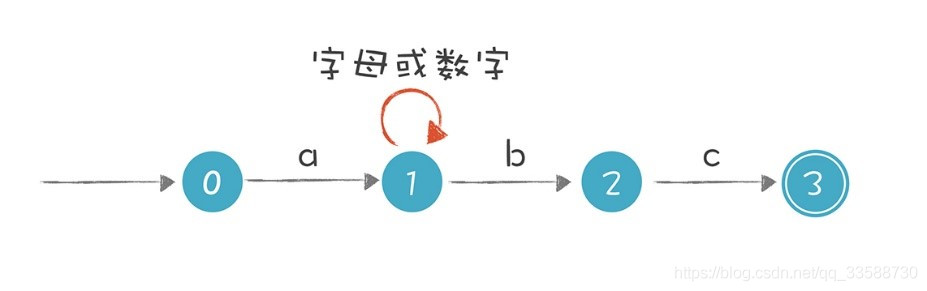
這個NFA還有引入ε轉換的畫法,它們是等價的。實際上第二個NFA可以用接下來提到的演算法,通過正則表達式自動生成出來,如下圖所示:
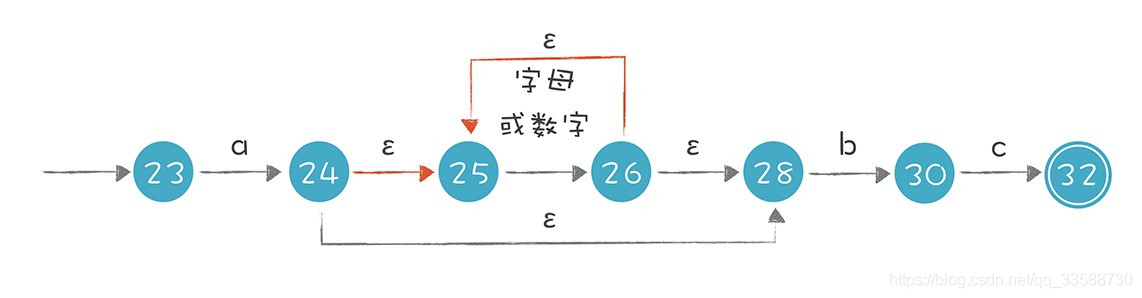
需要注意的是,無論是NFA還是DFA都等價於正則表達式,也就是所有的正則表達式都能轉換成NFA或DFA,反之亦然。
2. 理解了NFA和DFA之後,來看看如何從正則表達式生成NFA。需要把它分爲兩個子任務:
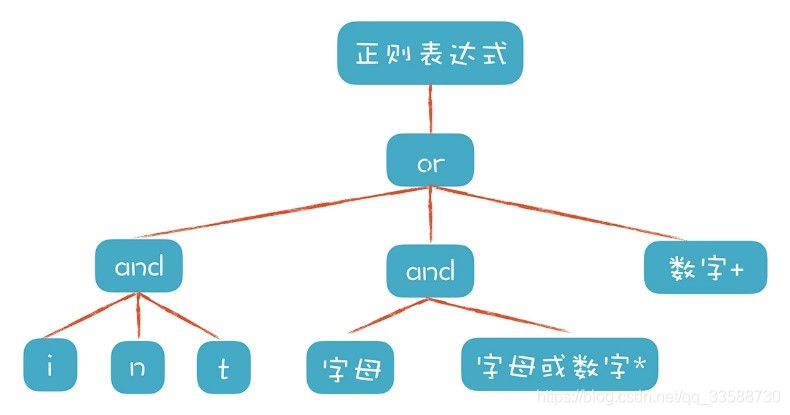
(1)把正則表達式解析成一個內部的數據結構,便於後續的程式使用。因爲正則表達式也是個字串,所以要先做一個小的編譯器,去理解代表正則表達式的字串。這裏偷個懶直接針對例子的正則表達式生成相應的數據結構,不需要做出這個編譯器。用來測試的正則表達式可以是int關鍵字、識別符號,或者數位字面量,如下所示:
int | [a-zA-Z][a-zA-Z0-9]* | [0-9]+
下面 下麪這段程式碼建立了一個樹狀的數據結構,來代表該正則表達式:
private static GrammarNode sampleGrammar1() {
GrammarNode node = new GrammarNode("regex1",GrammarNodeType.Or);
//int關鍵字
GrammarNode intNode = node.createChild(GrammarNodeType.And);
intNode.createChild(new CharSet('i'));
intNode.createChild(new CharSet('n'));
intNode.createChild(new CharSet('t'));
//識別符號
GrammarNode idNode = node.createChild(GrammarNodeType.And);
GrammarNode firstLetter = idNode.createChild(CharSet.letter);
GrammarNode letterOrDigit = idNode.createChild(CharSet.letterOrDigit);
letterOrDigit.setRepeatTimes(0, -1);
//數位字面量
GrammarNode literalNode = node.createChild(CharSet.digit);
literalNode.setRepeatTimes(1, -1);
return node;
}
列印輸出的結果如下:
RegExpression
Or
Union
i
n
t
Union
[a-z]|[A-Z]
[0-9]|[a-z]|[A-Z]*
[0-9]+
更直觀的示意圖如下所示:
(2)測試數據生成之後,把表示正則表達式的數據結構,轉換成一個NFA。這個過程比較簡單,因爲針對正則表達式中的每一個結構,都可以按照一個固定的規則做轉換。有這樣的幾個規則步驟:
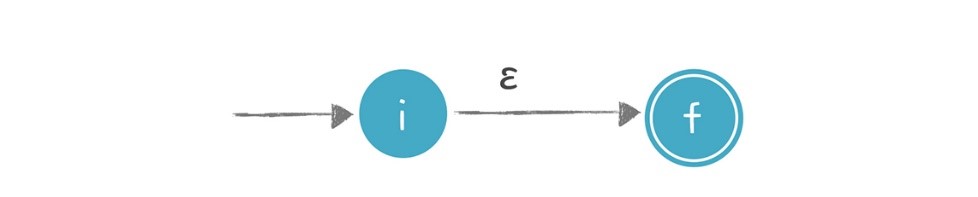
a. 識別ε的NFA:不接受任何輸入,也能從一個狀態遷移到另一個狀態,狀態圖的邊上標註ε,如下圖所示:
b. 識別i的NFA:當接受字元i時引發一個轉換,狀態圖的邊上標註i。如下圖所示:

c. 轉換「s|t」這樣的正則表達式:意思是或者s或者t,二者選一。s和t本身是兩個子表達式,可以增加兩個新的狀態:開始狀態和接受狀態(最終狀態)也就是下圖中帶雙線的狀態,它意味着被檢驗的字串此時符合正則表達式。然後用ε轉換分別連線代表s和t的子圖,即要麼走上面路徑那就是s,要麼走下面 下麪路徑那就是t:

d. 對於「?」「*」和「+」這樣的操作:意思是可以重複0次、0到多次、1到多次,轉換時要增加額外的狀態和邊。以「s*」爲例,做下面 下麪的轉換:
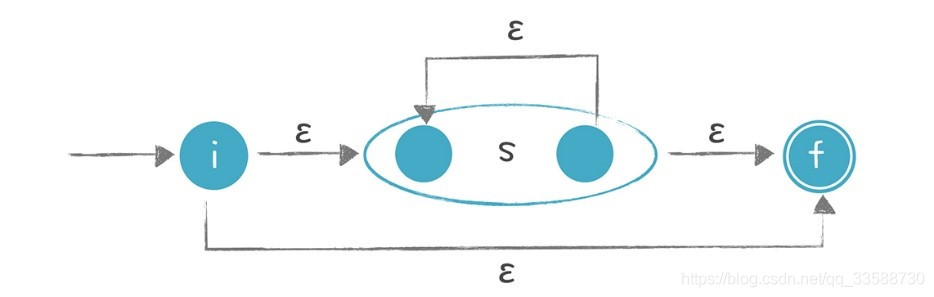
也就是它可以從i直接到 f,也就是對s匹配零次,也可以在s的起止節點上回圈多次。
3. 按照這些規則,可以編寫程式進行轉換。如下列程式碼所示:
public static State[] regexToNFA(GrammarNode node) {
State beginState = null;
State endState = null;
switch (node.getType()) {
//轉換s|t
case Or:
beginState = new State(); //新的開始狀態
endState = new State(true); //新的接受狀態
for (GrammarNode child : node.children()) {
//遞回,生成子圖,返回頭尾兩個狀態
State[] childState = regexToNFA(child);
//beginState,通過ε接到子圖的開始狀態
beginState.addTransition(new CharTransition(), childState[0]);
//子圖的結束狀態,通過ε接到endState
childState[1].addTransition(new CharTransition(), endState);
childState[1].setAcceptable(false);
}
break;
//轉換st
case And:
State[] lastChildState = null;
for (int i = 0; i < node.getChildCount(); i++) {
State[] childState = regexToNFA(node.getChild(i)); //生成子圖
if (lastChildState != null) {
//把前一個子圖的接受狀態和後一個子圖的開始狀態合併,把兩個子圖接到一起
lastChildState[1].copyTransitions(childState[0]);
lastChildState[1].setAcceptable(false);
}
lastChildState = childState;
if (i == 0) {
beginState = childState[0]; //整體的開始狀態
endState = childState[1];
} else {
endState = childState[1]; //整體的接受狀態
}
}
break;
//處理普通的字元
case Char:
beginState = new State();
endState = new State(true);
//圖的邊上是當前節點的charSet,也就是導致遷移的字元的集合,比如所有字母
beginState.addTransition(new CharTransition(node.getCharSet()), endState);
break;
}
State[] rtn = null;
//考慮重複的情況,增加必要的節點和邊
if (node.getMinTimes() != 1 || node.getMaxTimes() != 1) {
rtn = addRepitition(beginState, endState, node);
} else {
rtn = new State[]{beginState, endState};
}
//爲命了名的語法節點做標記,後面將用來設定Token型別。
if (node.getName() != null) {
rtn[1].setGrammarNode(node);
}
return rtn;
}
轉換完畢以後,將生成的NFA列印輸出,列出了所有的狀態,以及每個狀態到其他狀態的轉換,比如「0 ε -> 2」的意思是從狀態0通過ε轉換,到達狀態2 :
NFA states:
0 ε -> 2
ε -> 8
ε -> 14
2 i -> 3
3 n -> 5
5 t -> 7
7 ε -> 1
1 (end)
acceptable
8 [a-z]|[A-Z] -> 9
9 ε -> 10
ε -> 13
10 [0-9]|[a-z]|[A-Z] -> 11
11 ε -> 10
ε -> 13
13 ε -> 1
14 [0-9] -> 15
15 ε -> 14
ε -> 1
下面 下麪圖片直觀地展示了輸出結果,圖中分爲上中下三條路徑,能清晰地看出解析int關鍵字、識別符號和數位字面量的過程:

生成NFA之後,如何利用它識別某個字串是否符合這個NFA代表的正則表達式呢?以上圖爲例,當解析intA這個字串時,首先選擇最上面的路徑去匹配,匹配完int這三個字元以後來到狀態7,若後面沒有其他字元,就可以到達接受狀態1,返回匹配成功的資訊。可實際上,int後面是有A的,所以第一條路徑匹配失敗。失敗之後不能直接返回「匹配失敗」的結果,因爲還有其他路徑,所以要回溯到狀態0去嘗試第二條路徑,在第二條路徑中嘗試成功了。
執行Regex.java中的matchWithNFA()方法,可以用NFA來做正則表達式的匹配:
/**
* 用NFA來匹配字串
* @param state 當前所在的狀態
* @param chars 要匹配的字串,用陣列表示
* @param index1 當前匹配字元開始的位置。
* @return 匹配後,新index的位置。指向匹配成功的字元的下一個字元。
*/
private static int matchWithNFA(State state, char[] chars, int index1){
System.out.println("trying state : " + state.name + ", index =" + index1);
int index2 = index1;
for (Transition transition : state.transitions()){
State nextState = state.getState(transition);
//epsilon轉換
if (transition.isEpsilon()){
index2 = matchWithNFA(nextState, chars, index1);
if (index2 == chars.length){
break;
}
}
//消化掉一個字元,指針前移
else if (transition.match(chars[index1])){
index2 ++; //消耗掉一個字元
if (index2 < chars.length) {
index2 = matchWithNFA(nextState, chars, index1 + 1);
}
//如果已經掃描完所有字元
//檢查當前狀態是否是接受狀態,或者可以通過epsilon到達接受狀態
//如果狀態機還沒有到達接受狀態,本次匹配失敗
else {
if (acceptable(nextState)) {
break;
}
else{
index2 = -1;
}
}
}
}
return index2;
}
其中在匹配「intA」時,會看到它的回溯過程,如下所示:
NFA matching: 'intA'
trying state : 0, index =0
trying state : 2, index =0 //先走第一條路徑,即int關鍵字這個路徑
trying state : 3, index =1
trying state : 5, index =2
trying state : 7, index =3
trying state : 1, index =3 //到了末尾了,發現還有字元'A'沒有匹配上
trying state : 8, index =0 //回溯,嘗試第二條路徑,即識別符號
trying state : 9, index =1
trying state : 10, index =1 //在10和11這裏回圈多次
trying state : 11, index =2
trying state : 10, index =2
trying state : 11, index =3
trying state : 10, index =3
true
從中可以看到用NFA演算法的特點:因爲存在多條可能的路徑,所以需要試探和回溯,在比較極端的情況下,回溯次數會非常多,效能會變得非常慢。特別是當處理類似s*這樣的語句時,因爲s可以重0 到無窮次,所以在匹配字串時,可能需要嘗試很多次。注意在生成的NFA中,如果一個狀態有兩條路徑到其他狀態,演算法會依據一定的順序來嘗試不同的路徑。
9和11兩個狀態都有兩條向外走的線,其中紅色的線是更優先的路徑,也就是嘗試讓*號匹配儘量多的字元。這種演算法策略叫做「貪婪(greedy)」策略。在有的情況下,會希望讓演算法採用非貪婪策略,或者叫「忽略優先」策略,以便讓效率更高。有的正則表達式工具會支援多加一個?,比如??、*?、+?來表示非貪婪策略。
4. NFA的執行可能導致大量的回溯,所以能否將NFA轉換成DFA,讓字串的匹配過程更簡單呢?如果能的話,那整個過程都可以自動化,從正則表達式NFA,再從 NFA到DFA。這樣的演算法就是子集構造法,它的思路如下:
(1)首先NFA有一個初始狀態(從狀態0通過ε轉換可以到達的所有狀態,也就是說在不接受任何輸入的情況下,從狀態0也可以到達的狀態)。這個狀態的集合叫做「狀態0的ε閉包」,簡單一點稱之爲s0,s0包含0、2、8、14這幾個狀態,如下圖所示:
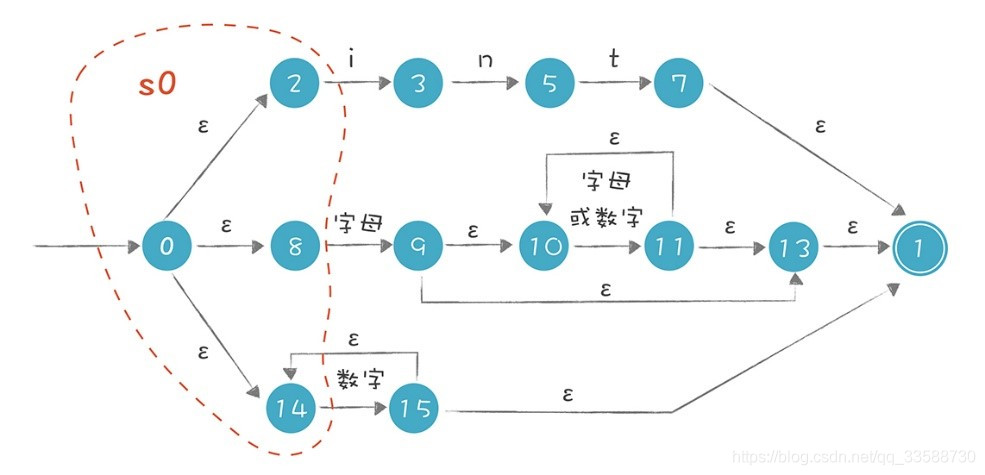
(2)將字母i給到s0中的每一個狀態,看它們能轉換成什麼狀態,再把這些狀態通過ε轉換就能到達的狀態也加入進來,形成一個包含「3、9、10、13、1」這5個狀態的集合s1。其中3和9是接受了字母i所遷移到的狀態,10、13、1是在狀態9的ε閉包中。如下圖所示:

(3)在s0和s1中間畫條遷移線,標註上i,意思是s0接收到i的情況下,轉換到s1:
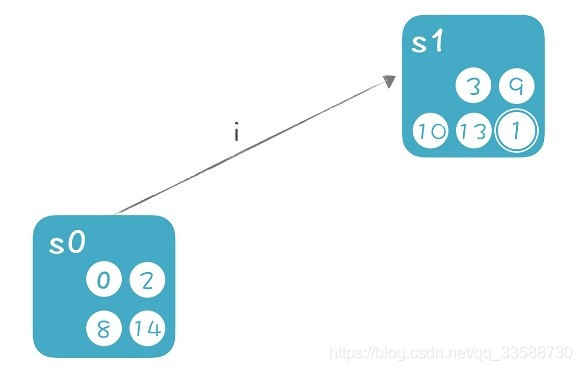
在這裏把s0和s1分別看成一個狀態。也就是說要生成的DFA,它的每個狀態,就是原來的NFA的某些狀態的集合。在上面的推導過程中,有兩個主要的計算:
(1)ε-closure(s),即集合s的ε閉包。也就是從集合s中的每個節點,加上從這個節點出發通過ε轉換所能到達的所有狀態。
(2)move(s,’i’),即從集合s接收一個字元i,所能到達的新狀態的集合。
按照上面的思路繼續推導,識別int關鍵字的識別路徑也就推導出來了,如下圖所示:

把上面這種推導的思路寫成演算法,NFA2DFA()函數的虛擬碼如下所示:
計算s0,即狀態0的ε閉包
把s0壓入待處理棧
把s0加入所有狀態集的集合S
回圈:待處理棧內還有未處理的狀態集
回圈:針對字母表中的每個字元c
回圈:針對棧裡的每個狀態集合s(i)(未處理的狀態集)
計算s(m) = move(s(i), c)(就是從s(i)出發,接收字元c能夠
遷移到的新狀態的集合)
計算s(m)的ε閉包,叫做s(j)
看看s(j)是不是個新的狀態集,如果已經有這個狀態集了,把它找出來
否則,把s(j)加入全集S和待處理棧
建立s(i)到s(j)的連線,轉換條件是c
執行NFA2DFA()方法,然後列印輸出生成的DFA。畫成圖就能很直觀地看出遷移的路徑了,如下圖所示:
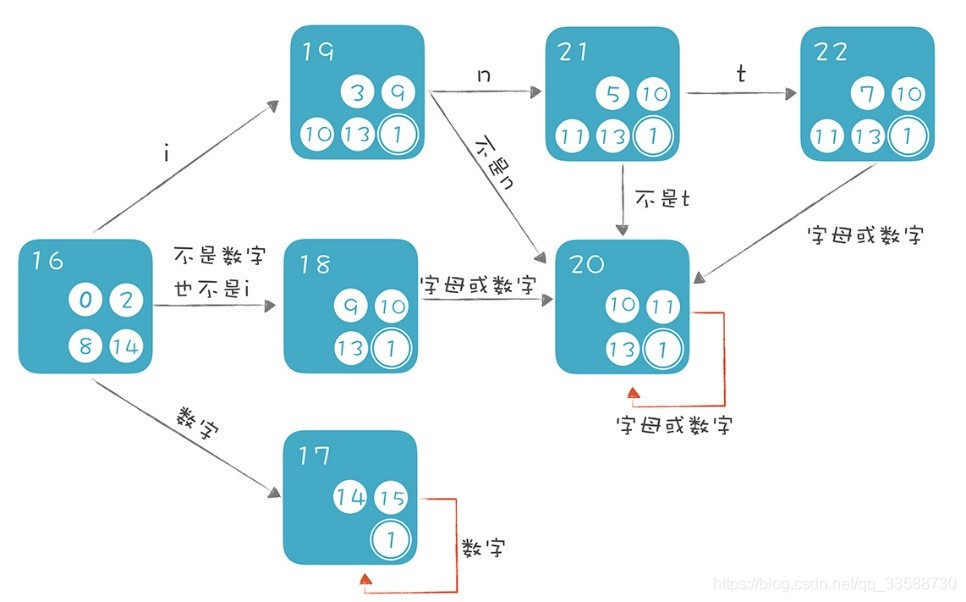
從初始狀態開始,如果輸入是i那就走int識別這條線,也就是按照19、21、22這條線依次遷移,如果中間發現不符合int模式,就跳轉到20也就是識別符號狀態。注意,在上面的DFA中,只要包含接受狀態1的,都是DFA的接受狀態。進一步區分的話,22是int關鍵字的接受狀態,因爲它包含了int關鍵字原來的接受狀態7。同理,17是數位字面量的接受狀態,18、19、20、21都是識別符號的接受狀態。
可以執行一下範例程式Regex.java中的matchWithDFA()的方法,看看效果:
private static boolean matchWithDFA(DFAState state, char[] chars, int index){
System.out.println("trying DFAState : " + state.name + ", index =" + index);
//根據字元,找到下一個狀態
DFAState nextState = null;
for (Transition transition : state.transitions()){
if (transition.match(chars[index])){
nextState = (DFAState)state.getState(transition);
break;
}
}
if (nextState != null){
//繼續匹配字串
if (index < chars.length-1){
return matchWithDFA(nextState,chars, index + 1);
}
else{
//字串已經匹配完畢
//看看是否到達了接受狀態
if(state.isAcceptable()){
return true;
}
else{
return false;
}
}
}
else{
return false;
}
}
執行時會列印輸出匹配過程,而執行過程中不產生任何回溯。現在可以自動生成DFA了,可以根據DFA做更高效的計算。不過有利就有弊,DFA也存在一些缺點。比如DFA可能有很多個狀態。假設原來NFA的狀態有n個,那麼把它們組合成不同的集合,可能的集合總數是2的n次方個。針對上面範例的NFA有13個狀態,所以最壞的情況下,形成的DFA可能有2的13次方,也就是8192個狀態,會佔據更多的記憶體空間。而且生成這個DFA本身也需要消耗一定的計算時間。當然這種最壞的狀態很少發生,上面範例的NFA生成DFA後,只有7個狀態。
因此,NFA和DFA有各自的優缺點:NFA通常狀態數量比較少,可以直接用來進行計算,但可能會涉及回溯,從而效能低下;DFA的狀態數量可能很大,佔用更多的空間,並且生成DFA本身也需要消耗計算資源。一般來說,正則表達式工具可以直接基於NFA。而詞法分析器(如Lex)則是基於DFA,因爲在生成詞法分析工具時,只需要計算一次DFA,就可以基於這個DFA做很多次詞法分析。
二、First和Follow集合:用LL演算法推演
5. 遞回下降演算法在語法分析階段生成AST時很常用,但會有回溯的現象,在效能上會有損失。所以要把演算法升級一下,實現帶有預測能力的自頂向下分析演算法,避免回溯。自頂向下分析的演算法是一大類演算法。總體來說,它是從一個非終結符出發,逐步推導出跟被解析的程式相同的Token串。這個過程可以看做是一張圖的搜尋過程,這張圖非常大,因爲針對每一次推導,都可能產生一個新節點,如下圖所示:

演算法的任務就是在大圖中,找到一條路徑,能產生某個句子(Token串)。比如上圖找到了三條紅色的路徑,都能產生「2+3*5」這個表達式。
根據搜尋的策略,有深度優先(Depth First)和廣度優先(Breadth First)兩種,這兩種策略的推導過程是不同的。深度優先是沿着一條分支把所有可能性探索完,以「add->mul+add」產生式爲例,它會先把mul這個非終結符展開,比如替換成pri,然後再把它的第一個非終結符pri展開。只有把這條分支都向下展開之後,纔會回到上一級節點,去展開它的兄弟節點。遞回下降演算法就是深度優先的,這也是它不能處理左遞回的原因,因爲左邊的分支永遠也不能展開完畢。
而針對「add->add+mul」這個產生式,廣度優先會把add和mul這兩個都先展開,這樣就形成了四條搜尋路徑,分別是mul+mul、add+mul+mul、add+pri和add+mul*pri。接着把它們的每個非終結符再一次展開,會形成18條新的搜尋路徑。所以廣度優先遍歷需要探索的路徑數量會迅速爆炸,成指數級上升。哪怕用下面 下麪這個最簡單的語法,去匹配「2+3」表達式,都需要嘗試20多次,更別提針對更復雜表達式或採用更復雜的語法規則了:
//一個很簡單的語法
add -> pri //1
add -> add + pri //2
pri -> Int //3
pri -> (add) //4
這樣看來,指數級上升的記憶體消耗和計算量,使得廣度優先在這方面根本沒有實用價值。雖然上面的演算法有優化空間,但無法從根本上降低演算法複雜度。當然它也有可以使用左遞回文法的優點,不過並不會爲了這個優點去忍受演算法的效能問題。而深度優先演算法在記憶體佔用上是線性增長的。考慮到回溯的情況,在最壞情況下它的計算量也會指數式增長,但可以通過優化讓複雜度降爲線性增長。
針對深度優先演算法的優化方向是減少甚至避免回溯,思路就是給演算法加上預測能力。比如在解析statement時,看到一個if,就知道肯定這是一個條件語句,不用再去嘗試其他產生式了。LL演算法就屬於這類預測性的演算法。第一個L是Left-to-right,代表從左向右處理程式程式碼。第二個L是Leftmost,意思是最左推導。
按照語法規則,一個非終結符展開後會形成多個子節點,其中包含終結符和非終結符。最左推導是指,從左到右依次推導展開這些非終結符。採用Leftmost的方法,在推導過程中句子的左邊逐步都會被替換成終結符,只有右邊的纔可能包含非終結符。以「2+3*5」爲例,它的推導順序從左到右,非終結符逐步替換成了終結符:
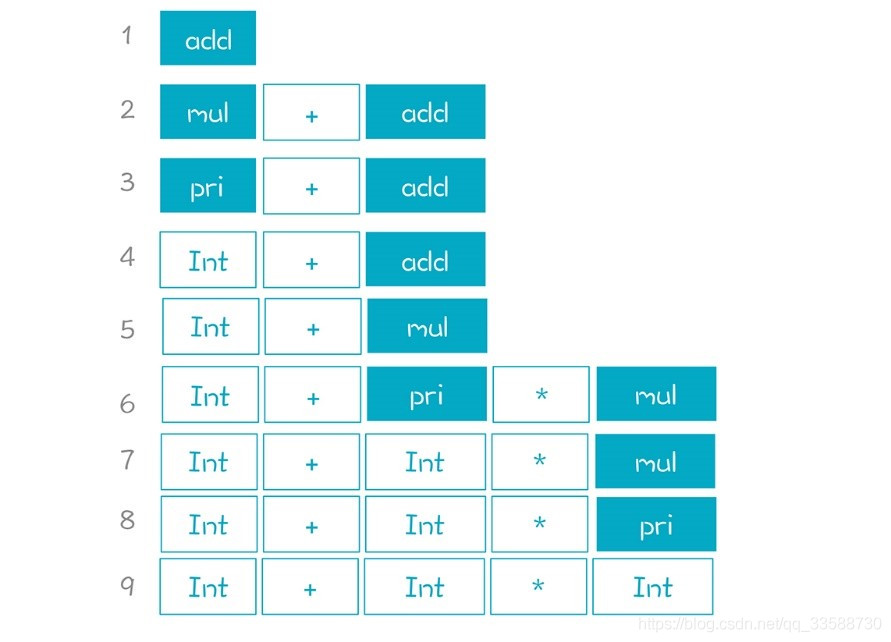
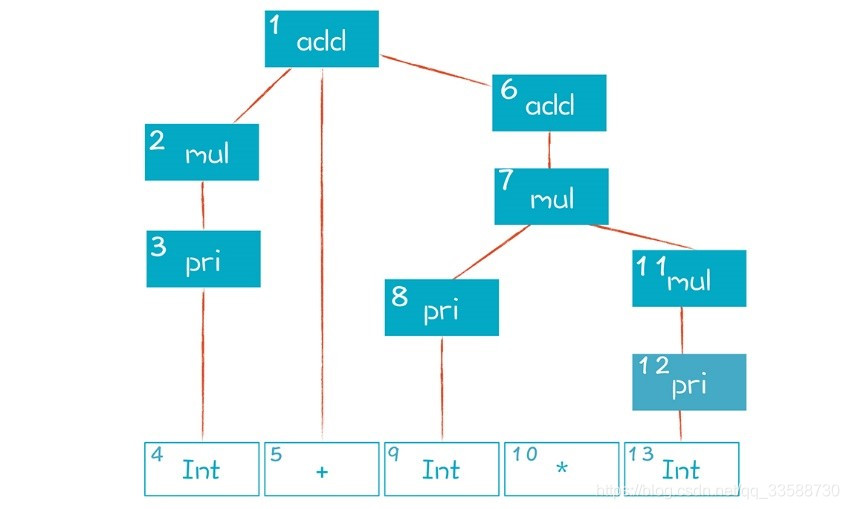
下圖是上述推導過程建立起來的AST,「1、2、3……」等編號是AST節點建立的順序:
6. 上面把自頂向下分析演算法做了總體概述,並講了最左推導的含義,現在來看看LL演算法到底是什麼。LL演算法是帶有預測能力的自頂向下演算法。在推導時希望當存在多個候選的產生式時,瞄一眼下一個(或多個)Token,就知道採用哪個產生式。如果只需要預看一個Token,就是LL(1)演算法。拿statement的語法舉例,它有好幾個產生式,分別產生if 語句、while語句、switch語句等,如下所示:
statement
: block
| IF parExpression statement (ELSE statement)?
| FOR '(' forControl ')' statement
| WHILE parExpression statement
| DO statement WHILE parExpression ';'
| SWITCH parExpression '{' switchBlockStatementGroup* switchLabel*
| RETURN expression? ';'
| BREAK IDENTIFIER? ';'
| CONTINUE IDENTIFIER? ';'
| SEMI
| statementExpression=expression ';'
| identifierLabel=IDENTIFIER ':' statement
;
如果看到下一個Token是if,那麼後面跟着的肯定是if語句,這樣就實現了預測,不需要一個個產生式去試。問題來了,if語句的產生式的第一個元素就是一個終結符,這自然很好判斷,可如果是一個非終結符比如表達式語句,該怎麼判斷呢?
其實可以爲statement的每條分支計算一個集合,集合包含了這條分支所有可能的起始Token。如果每條分支的起始Token是不一樣的,也就是這些集合的交集是空集,那麼就很容易根據這個集合來判斷該選擇哪個產生式,把這樣的集合就叫做這個產生式的First集合。First集合的計算很直觀,假設要計算的產生式是x:
(1)如果x以Token開頭,那麼First(x)包含的元素就是這個Token,比如if語句的First集合就是{IF}。
(2)如果x的開頭是非終結符a,那麼First(x)要包含First(a)的所有成員。比如expressionStatment是以expression開頭,因此它的First集合要包含First(expression)的全體成員。
(3)如果x的第一個元素a能夠產生ε,那麼還要再往下看一個元素b,把First(b)的成員也加入到First(x),以此類推。如果所有元素都可能返回ε,那麼First(x)也應該包含ε,意思是x也可能產生ε。比如下面 下麪的blockStatements產生式,它的第一個元素是blockStatement*,也就意味着blockStatement的數量可能爲0,因此可能產生ε。那麼First(blockStatements) 除了要包含First(blockStatement)的全部成員,還要包含後面的「;」,如下所示:
blockStatements
: blockStatement*
;
(4)如果x是一個非終結符,它有多個產生式可供選擇,那麼First(x)應包含所有產生式的First()集合的成員。比如statement的First集合要包含if、while等所有產生式的First集合的成員。並且如果這些產生式只要有一個可能產生ε,那麼x就可能產生ε,因此First(x)就應該包含ε。
在這裏的範例中,可以用SampleGrammar.expressionGrammar()方法獲得一個表達式的語法,把它dump()一下,這其實是消除了左遞回的表達式語法:
expression : assign ;
assign : equal | assign1 ;
assign1 : '=' equal assign1 | ε;
equal : rel equal1 ;
equal1 : ('==' | '!=') rel equal1 | ε ;
rel : add rel1 ;
rel1 : ('>=' | '>' | '<=' | '<') add rel1 | ε ;
add : mul add1 ;
add1 : ('+' | '-') mul add1 | ε ;
mul : pri mul1 ;
mul1 : ('*' | '/') pri mul1 | ε ;
pri : ID | INT_LITERAL | LPAREN expression RPAREN ;
用GrammarNode類代表語法的節點,形成一張語法圖(藍色節點的下屬節點之間是「或」的關係,也就是語法中的豎線),如下圖所示:

基於這個數據結構能計算每個非終結符的First集合,在計算時要注意,因爲上下文無關文法是允許遞回巢狀的,所以這些GrammarNode節點構成的是一個圖而不是樹,不能通過簡單的遍歷樹的方法來計算First集合。比如pri節點是expression的後代節點,但pri又參照了expression(pri->(expression))。這樣,計算First(expression)需要用到First(pri),而計算First(pri)又需要依賴First(expression)。
破解這個僵局的方法是用「不動點法」來計算。多次遍歷圖中的節點,看看每次有沒有計算出新的集合成員。比如第一遍計算時,當求First(pri)的時候,它所依賴的First(expression)中的成員可能不全,等下一輪繼續計算時,發現有新的集合成員再加進來就好了,直到所有集合的成員都沒有變動爲止。
7. 現在可以用First集合進行分支判斷了,不過還要處理產生式可能爲ε的情況,比如「+mul add1 | ε」或「blockStatement*」都會產生ε。對ε的處理分成兩種情況:
(1)產生式中的部分元素會產生ε。比如在Java語法裡宣告一個類成員時,可能會用public、private等來修飾,但也可以省略不寫。在語法規則中這個部分是「accessModifier?」,它就可能產生ε,如下所示:
memberDeclaration : accessModifier? type identifier ';' ;
accessModifier : 'public' | 'private' ;
type : 'int' | 'long' | 'double' ;
所以當遇到下面 下麪這兩個語句時,都可以判斷爲類成員的宣告:
public int a;
int b;
這時,type能夠產生的終結符‘int’、‘long’和‘double’也在memberDeclaration的First集閤中。這樣實際上把accessModifier給穿透了,直接到了下一個非終結符type。所以這類問題依靠First集合仍然能解決。在解析的過程中,如果下一個Token是‘int’,可以認爲accessModifier返回了ε,忽略它繼續解析下一個元素type,因爲它的First集閤中纔會包含‘int’。
(2)產生式本身(而不是其組成部分)產生ε。這類問題僅僅依靠First集合是無法解決的,要引入另一個集合:Follow集合。它是所有可能跟在某個非終結符之後的終結符的集合。以block語句爲例,在PlayScript.g4中,大致是這樣定義的:
block
: '{' blockStatements '}'
;
blockStatements
: blockStatement*
;
blockStatement
: variableDeclarators ';'
| statement
| functionDeclaration
| classDeclaration
;
也就是說,block是由blockStatements構成的,而blockStatements可以由0到n個blockStatement構成,因此可能產生ε。接下來看看解析block時會發生什麼,假設花括號中一個語句也沒有,也就是blockStatments實際上產生了ε,那麼在解析block時,首先讀取了一個Token即「{」,然後處理blockStatements,再預讀一個Token發現是「}」,那這個右花括號是blockStatement的哪個產生式的呢?實際上它不在任何一個產生式的First集閤中,下面 下麪是進行判斷的虛擬碼:
nextToken = tokens.peek(); //得到'}'
nextToken in First(variableDeclarators) ? //no
nextToken in First(statement) ? //no
nextToken in First(functionDeclaration) ? //no
nextToken in First(classDeclaration) ? //no
找不到任何一個可用的產生式。這可怎麼辦呢?除了可能是blockStatments本身產生了ε之外,還有一個可能性就是出現語法錯誤了。而要繼續往下判斷,就需要用到Follow集合。像blockStatements的Follow集合只有一個元素,就是右花括號「}」。所以只要再檢查一下nextToken是不是花括號就行了:
//虛擬碼
nextToken = tokens.peek(); //得到'}'
nextToken in First(variableDeclarators) ? //no
nextToken in First(statement) ? //no
nextToken in First(functionDeclaration) ? //no
nextToken in First(classDeclaration) ? //no
if (nextToken in Follow(blockStatements)) //檢查Follow集合
return Epsilon; //推導出ε
else
error; //語法錯誤
計算非終結符x的Follow集合,有如下的規則:
(1)掃描語法規則,看看x後面都可能跟哪些符號。
(2)對於後面跟着的終結符,都加到Follow(x)集閤中去。
(3)如果後面是非終結符,就把它的First集合加到自己的Follow集閤中去。
(4)最後,如果後面的非終結符可能產出ε,就再往後找,直到找到程式終結符號。
這個符號通常記做$,意味一個程式的結束。比如在表達式的語法裡,expression後面可能跟這個符號,expression的所有右側分支的後代節點也都可能跟這個符號,也就是它們都可能出現在程式的末尾。但另一些非終結符後面不會跟這個符號,如blockstatements,因爲它後面肯定會有「}」。這裏也要用到不動點法做計算。執行程式可以列印出範例語法的的Follow集合。程式列印輸出的First和follow集合整理如下(列印輸出還包含一些中間節點,這裏省略):

在表達式的解析中,會綜合運用First和Follow集合。比如對於「add1 -> + mul add1 | ε」,如果預讀的下一個Token是+,那就按照第一個產生式處理,因爲+在First(「+ mul add1」)集閤中。如果預讀的Token是>號,那它肯定不在First(add1)中,而要看它是否屬於Follow(add1),如果是那麼add1就產生一個ε,否則就報錯。
8. 現在已經建立了對First集合、Follow集合和LL演算法計算過程的直覺認知,這樣再寫出演算法的實現就比較容易了。用LL演算法解析語法時,可以選擇兩種實現方式:
(1)還是採用遞回下降演算法,只不過現在的遞回下降演算法是沒有任何回溯的。無論走到哪一步,都能準確地預測出應該採用哪個產生式。
(2)採用表驅動的方式。這個時候需要基於計算出來的First和Follow集合構造一張預測分析表。根據這個表查詢在遇到什麼Token的情況下,應該走哪條路徑。
這兩種方式是等價的,接下來談談如何設計符合LL(k)特別是LL(1)演算法的文法。前面已經知道左遞回的文法是要避免的,除此之外要儘量抽取左公因子,這樣可以避免First集合產生交集。舉例來說,變數宣告和函數宣告的規則在前半截都差不多,都是型別後面跟着識別符號:
statement : variableDeclare | functionDeclare | other;
variableDeclare : type Identifier ('=' expression)? ;
funcationDeclare : type Identifier '(' parameterList ')' block ;
具體程式碼例子如下:
int age;
int cacl(int a, int b){
return a + b;
}
這樣的語法規則如果按照LL(1)演算法,First(variableDeclare)和First(funcationDeclare)是相同的,沒法決定走哪條路徑。就算用LL(2)也是一樣的,要用到LL(3)才行。但對於LL(k) k > 1來說,程式開銷有點大,因爲要計算更多的集合,構造更復雜的預測分析表。不過這個問題容易解決,只要把它們的左公因子提出來就可以了:
statement: declarator | other;
declarator : declarePrefix (variableDeclarePostfix
|functionDeclarePostfix) ;
variableDeclarePostfix : ('=' expression)? ;
functionDeclarePostfix : '(' parameterList ')' block ;
這樣,解析程式先解析它們的公共部分即declarePrefix,然後再看後面的差異。這時它倆的First集合,一個是{ = ; },一個是{ ( },兩者沒有交集能夠很容易區分。
三、移進和歸約:用LR演算法推演
9. 前面討論的語法分析演算法都是自頂向下的。與之對應的是自底向上的演算法,比如LR演算法,它能夠支援更多的語法,而且沒有左遞回的問題。第一個字母L與LL演算法的第一個L一樣,代表從左向右讀入程式。第二個字母R,指的是RightMost(最右推導),也就是在使用產生式時,是從右往左依次展開非終結符,例如對於「add->add+mul」這樣一個產生式,是優先把mul展開然後再是add。
自頂向下的演算法,是遞回地做模式匹配,從而逐步地構造出AST。那麼自底向上的演算法是如何構造出AST的呢?答案是用移進-規約的演算法。先通過一個例子看自底向上語法分析的過程,如下所示:
add -> mul
add -> add + mul
mul -> pri
mul -> mul * pri
pri -> Int | (add)
然後來解析「2+3*5」這個表達式,AST如下,分步驟看一下解析的具體過程:

(1)看到第一個Token是Int即2,把它作爲AST的第一個節點,同時把它放到一個棧裡(下圖紅線左邊的部分)。這個棧代表着正在處理的一些AST節點,把Token移到棧裡的動作叫做移進(Shift)。

(2)根據語法規則,Int是從pri推導出來的(pri->Int),那麼它的上級AST肯定是pri,所以給它加了一個父節點pri,同時也把棧裡的Int替換成了pri。這個過程是語法推導的逆過程,叫做規約(Reduce),如下圖所示:

具體來講,它是從工作區裡倒着取出1到n個元素,根據某個產生式組合出上一級的非終結符,也就是AST的上級節點,然後再放進工作區(也就是上面豎線的左邊)。這個時候棧裡可能有非終結符,也可能有終結符,它彷彿是組裝AST的一個工作區,豎線的右邊全都是Token(即終結符),它們在等待處理。
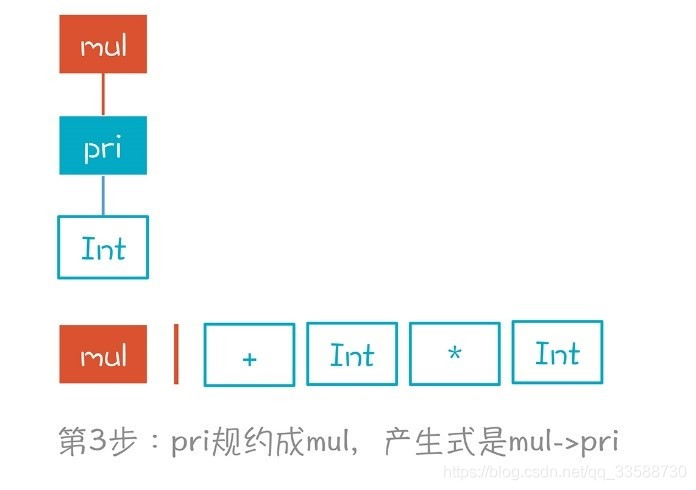
(3)與第2步一樣,因爲pri只能是mul推導出來的,即產生式是「mul->pri」,所以又做了一次規約,如下圖所示:
(4)根據「add->mul」產生式,將mul規約成add。至此對第一個Token做了3次規約,已經到頭了。這裏爲什麼做規約,而不是停在mul上移進+號,是有原因的。因爲沒有一個產生式是mul後面跟+號,而add後面卻可以跟+號,如下圖所示:

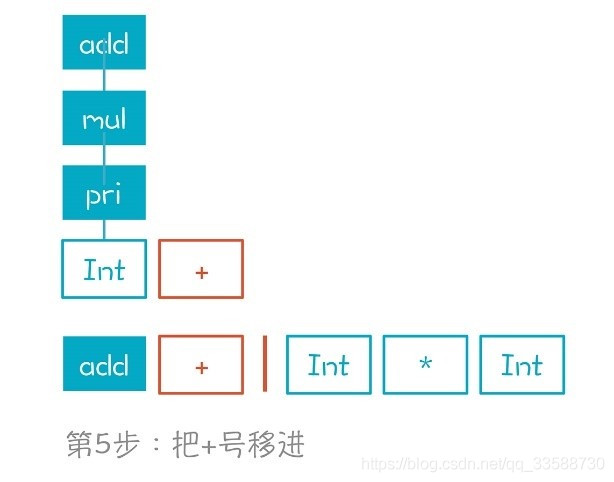
(5)移進+號。現在棧裡有兩個元素了,分別是add和+,如下圖所示:
(6)移進Int也就是數位3。棧裡現在有3個元素,如下圖所示:
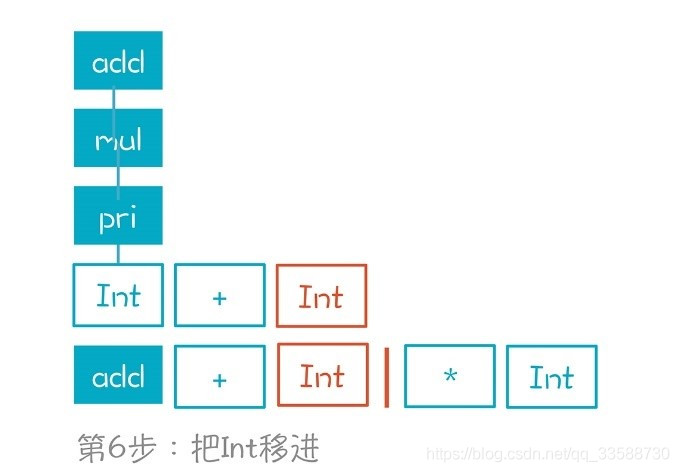
(7)&(8)將Int規約到pri再規約到mul。到目前爲止做規約的方式都比較簡單,就是對着棧頂的元素,把它反向推導回去,如下圖所示:
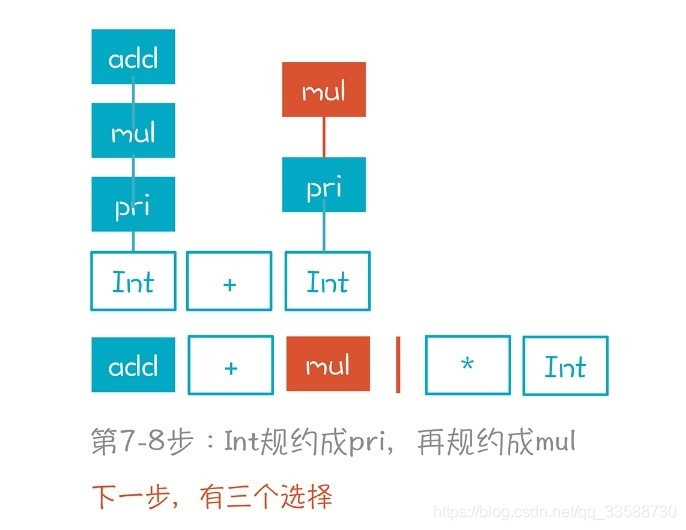
(9)面臨3個選擇。第一個選擇是繼續把mul規約成add,第二個選擇是把「add+mul」規約成add。這兩個選擇都是錯誤的,因爲它們最終無法形成正確的AST,如下圖所示:

第三個選擇,也就是按照「mul->mul*pri」繼續移進*號而不是做規約。只有這樣才能 纔能形成正確的AST,就像下圖中的虛線:

(10)移進Int也就是數位5,如下圖所示:

(11)Int規約成pri,如下圖所示:
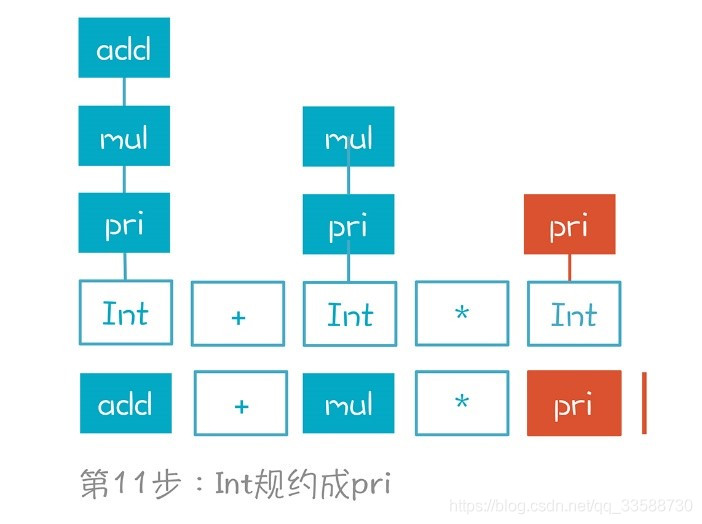
(12)mul*pri規約成mul。注意這裏也有兩個選擇,比如把pri繼續規約成mul,但它顯然也是錯誤的選擇,如下圖所示:

(13)add+mul規約成add,如下圖所示:

至此就構建完成了一棵正確的AST,並且棧裡也只剩下了一個元素,就是根節點。
10. 上面整個語法解析過程,實質是反向最右推導(Reverse RightMost Derivation),即如果把AST節點根據建立順序編號,就是下面 下麪這張圖呈現的樣子,根節點編號最大是13:

但這是規約的過程,如果是從根節點開始的推導過程,順序恰好是反過來的,先是13號再是右子節點12號,再是12號的右子節點11號,以此類推。這個最右推導過程如下:

在語法解析時是從底下反推回去,所以叫做反向的最右推導過程。從這個意義上講,LR演算法中的R帶有反向(Reverse)和最右(Reightmost)這兩層含義。在最右推導過程中,加了下劃線的部分叫做一個控制代碼(Handle)。控制代碼是一個產生式的右邊部分,以及它在一個右句型(最右推導可以得到的句型)中的位置。以最底下一行爲例,這個控制代碼「Int」是產生式「pri->Int」的右邊部分,它的位置是句型「Int + Int * Int」的第一個位置。簡單來說,控制代碼就是產生式是在這個位置上做推導的,如果需要做反向推導的話,也是從這個位置去做規約。
11. 要把這種判斷過程變成嚴密的演算法,做到在每一步都知道該做移進還是規約,做規約該按照哪個產生式,這就是LR演算法要解決的核心問題了。那麼如何找到正確的控制代碼呢?最右推導是從最開始的產生式出發,經過多步推導(記作->*),一步步形成當前的局面(即左邊棧裡有一些非終結符和終結符,右邊還可以預看1到k個Token),如下所示:
add ->* 棧 | Token
根據手頭掌握的資訊,可以反向推導出這個多步推導的路徑,從而獲得正確的控制代碼。這裏依據的是左邊棧裡的資訊,以及右邊的Token串。對於LR(0)演算法來說,只依據左邊的棧就能找到正確的控制代碼,對於LR(1)演算法來說,可以從右邊預看一個Token。思路是根據語法規則復現這條推導路徑。以上面第8步爲例,下圖是它的推導過程,紅色的路徑是唯一能夠到達第8步的路徑。知道了正向推導的路徑,在第8步正確的選擇是做移進:
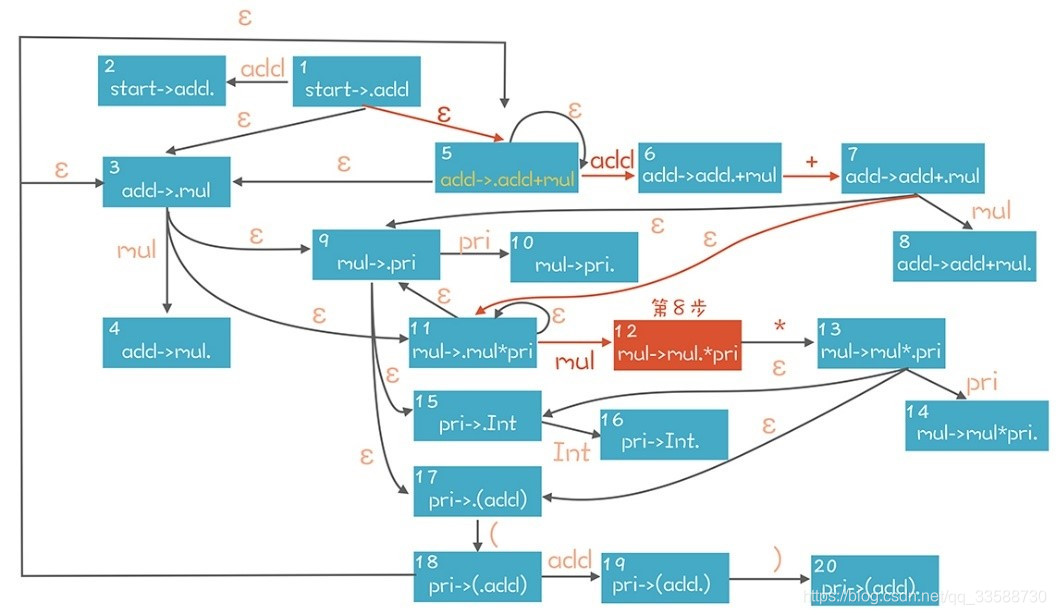
爲了展示這個推導過程,這裏引入一個新概念:專案(Item)。Item代錶帶有「.」符號的產生式。比如「pri->(add)」可以產生4個Item,「.」分別在不同的位置。「.」可以看做是之前步驟示意圖中的豎線,左邊的看做已經在棧裡的部分,「.」右邊的看做是期待獲得的部分:
pri->.(add)
pri->(.add)
pri->(add.)
pri->(add).
上圖其實是一個NFA,利用這個NFA表達了所有可能的推導步驟。每個Item(或者狀態)在接收到一個符號時,就遷移到下一個狀態,比如「add->.add+mul」在接收到一個add時就遷移到「add->add.+mul」,再接收到一個「+」就遷移到「add->add+.mul」。
在這個狀態圖的左上角,用一個輔助性的產生式「start->add」作爲整個 NFA 的唯一入口。從這個入口出發,可以用這個NFA來匹配棧裡內容,比如在第 8 步的時候,棧以及右邊下一個 Token 的狀態如下,其中豎線左邊是棧的內容:
add + mul | *
在NFA中,從start開始遍歷,基於棧裡的內容能找到圖中紅色的多步推導路徑。在這個狀態遷移過程中,導致轉換的符號分別是「ε、add、+、ε、mul」,忽略其中的ε就是棧裡的內容。在NFA中,查詢到的Item是「mul->mul.*pri」。這個時候「.」在Item的中間。因此下一個操作只能是一個Shift操作,也就是把下一個Token即*號移進到棧裡。如果「.」在Item的最後則對應一個規約操作,比如在第12步,棧裡的內容是:
add + mul | $ //$代表Token串的結尾

這個時候的Item是「add->add+mul.」。對於所有點符號在最後面的Item,已經沒有辦法繼續向下遷移了,這個時候需要做一個規約操作,也就是基於「add + mul」規約到add,也就是到「add->.add+mul」這個狀態。對於任何的ε轉換,其逆向操作也是規約,比如圖中從「add->.add+mul」規約到「start->.add」。但做規約操作之前,仍然需要檢查後面跟着的Token是不是在Follow(add)中。對於add來說,它的Follow集合包括{ $ + ) },如果是這些Token那就做規約,否則就報編譯錯誤。
當然,每個NFA都可以轉換成一個DFA。所以可以直接在上面的NFA裡去匹配,也可以把NFA轉成DFA,避免NFA的回溯現象,讓演算法效率更高。轉換完畢的DFA如下:
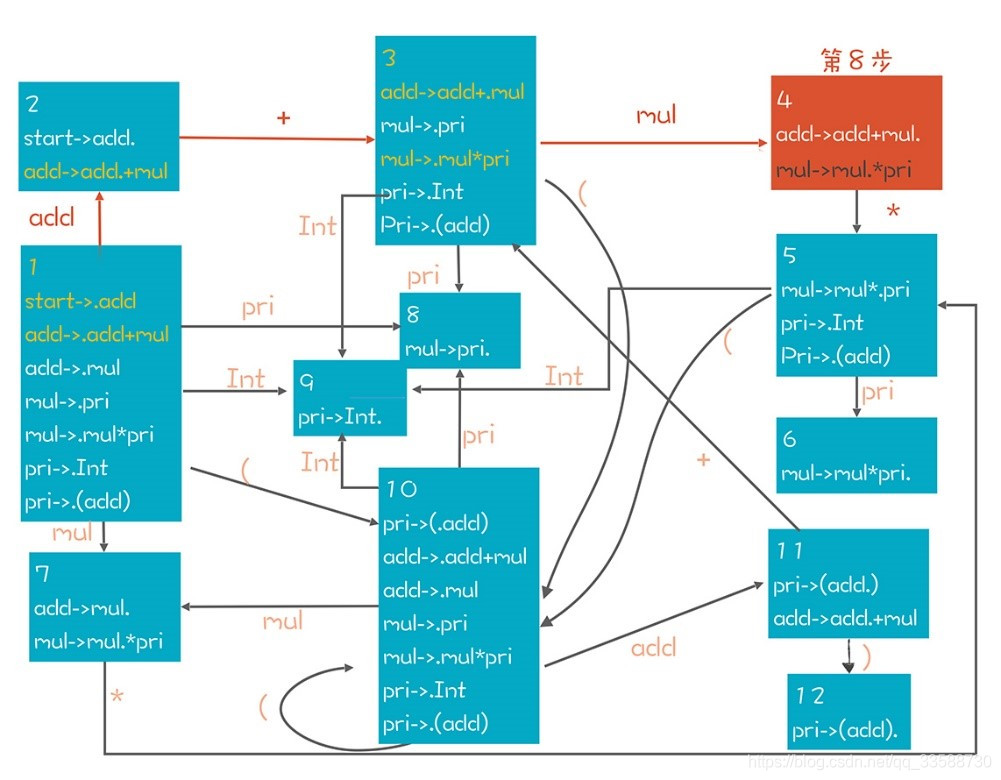
在這個DFA中同樣標註了在第8步時的推導路徑。爲了更清晰地理解LR演算法的本質,基於這個DFA再把語法解析的過程推導一遍:
(1)移進一個Int,從狀態1遷移到9。Item是「pri->Int.」。

(2)依據「pri->Int」做規約,從狀態9回到狀態1。因爲現在棧裡有個pri元素,所以又遷移進了狀態8。

(3)依據「mul->pri」做規約,從狀態8回到狀態1,再根據棧裡的mul元素進入狀態7。注意在狀態7的時候,下一步的走向有兩個可能的方向,分別是「add->mul.」和「mul->mul.*pri」這兩個Item代表的方向。基於「add->mul.」會做規約,而基於「mul->mul.*pri」會做移進,這就需要看看後面的Token了。如果後面的Token是*號,那其實要選第二個方向。但現在後面是+號,所以意味着這裏只能做規約。

(4)依據「add->mul」做規約,從狀態7回到狀態1,再依據add元素進入狀態2。

(5)移進+號。這對應狀態圖上的兩次遷移,首先根據棧裡的第一個元素add從1遷移到2。然後再根據「+」從2到3。Item的變化是:
狀態 1:start->.add
狀態 1:add->.add+mul
狀態 2:add->add.+mul
狀態 3:add->add+.mul
通過移進這個加號,實際上知道了這個表達式頂部必然有一個「add+mul」的結構。

(6)~(8)移進Int,並一直規約到mul。狀態變化是先從狀態3到狀態9,然後回到狀態3,再進到狀態4。
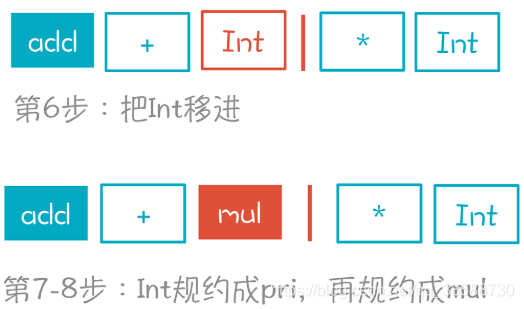
(9)移進一個*。根據棧裡的元素,遷移路徑是 1->2->3->4->5。

(10)移進Int進入狀態9。

(11)根據「pri->Int」規約到pri,先退回到狀態5,接着根據pri進入狀態6。

(12)根據「mul->mul*pri」規約到mul,從而退回到狀態4。

(13)根據「add->add+mul」規約到add,從而退回到狀態2。

從狀態2再根據「start->add」再規約一步就變成了start,回到狀態1解析完成。
12. LR演算法根據能力的強弱和實現的複雜程度,可以分成多個級別,分別是LR(0)、SLR(k)(即簡單 LR)、LALR(k)(Look ahead LR)和LR(k),其中k表示要在Token佇列裡預讀k個Token。下面 下麪講解一下這幾種型別演算法的特點:

(1)LR(0)不需要預看右邊的 Token,僅僅根據左邊的棧進行反向推導。比如,前面DFA中的狀態8只有一個Item:「mul->pri.」。如果處在這個狀態,那接下來操作是規約。假設存在另一個狀態,它也只有一個Item,點符號不在末尾,比如「mul->mul.*pri」,那接下來的操作就是移進,把下一個輸入放到棧裡。
但實際使用的語法規則很少有這麼簡單的。所以LR(0)的表達能力太弱,能處理的語法規則有限,不太有實用價值。就像在前面的例子中,如果不往下預讀一個Token,僅僅利用左邊工作區的資訊,是找不到正確的控制代碼的。比如在狀態7中,可以做兩個操作:對於第一個Item即「add->mul.」,需要做一個規約操作;對於第二個Item即「mul->mul.*pri」,實際上需要做一個移進操作。
這裏發生的衝突,就叫做「移進/規約」衝突(Shift/Reduce Conflict),意思是又可以做移進又可以做規約,對於狀態7來說,到底做哪個操作實際上取決於右邊的Token。
(2)SLR(Simple LR)是在LR(0)的基礎上做了增強。對於狀態7的這種情況要加一個判斷條件:右邊下一個輸入的Token,是不是在add的Follow集閤中。因爲只有這樣做規約纔有意義。在例子中,add的Follow集合是{+ ) $},如果不在這個範圍內,那麼做規約肯定是不合法的。因爲Follow集合的意思,就是哪些Token可以出現在某個非終結符後面。所以如果在狀態7中下一個Token是*,它不在add的Follow集閤中,那麼就只剩了一個可行的選擇就是移進。這樣就不存在兩個選擇,也不存在衝突。
實際上,就這裏所用的範例語法而言,SLR就足夠了,但是對於一些更復雜的語法,採用SLR仍然會產生衝突,比如:
start -> exp
exp -> lvalue = rvalue
exp -> rvalue
lvalue -> Id
lvalue -> *rvalue
rvalue -> lvalue
這個語法說的是關於左值和右值的情況,在這裏的範例語法裡,右值只能出現在賦值符號右邊。在狀態2如果下一個輸入是「=」,那麼做移進和規約都是可以的。因爲「=」在rvalue的Follow集閤中,如下圖所示:

(3)怎麼來處理這種衝突呢?僅僅根據Follow集合來判斷是否Reduce不太嚴謹。因爲在上圖狀態2的情況下,即使後面跟着的是「=」仍然不能做規約。因爲一規約就成了一個右值,但它在等號的左邊,顯然是跟上面的語法定義衝突的。辦法是Follow集合拆了,把它的每個成員都變成Item的一部分。這樣就能做更細緻的判斷。如下圖所示,這樣細化以後,發現在狀態2中只有下一個輸入是「$」的時候才能 纔能做規約。這就是LR(1)演算法的原理,它更加強大:

但LR(1)演算法也有一個缺點,就是DFA可能會很大。在語法分析階段,DFA的大小會隨着語法規則的數量呈指數級上升,一個典型的語言的DFA狀態可能達到上千個,這會使語法分析的效能很差,從而也喪失了實用性。
(4)LALR(k)是基於這個缺點做的改進。它用了一些技巧能讓狀態數量變得比較少,但處理能力沒有太大的損失,YACC和Bison這兩個工具就是基於LALR(1)演算法的。