用C語言實現簡單的多元線性迴歸演算法(二)
2020-08-12 22:50:15
上一篇我們貼上了簡單粗暴的線性迴歸的程式碼,裏面各種參數都設定的是固定參數,不具有可延伸性,今天我們在上一篇的基礎上做了部分改進,當然對於熟悉C語言的大俠來說可能這篇部落格會太low了,您完全可以跳過。我們在這裏只是講如何用C語言自己實現一個有實用性的線性迴歸。有人會說用python不是很簡單嗎,幹嘛費勁巴拉的用C語言實現。首先這裏是爲了滿足某些只支援C語言的環境,例如IOT的部分裝置;另外也是爲了加深對演算法的理解和思考。至於線性迴歸原理網上到處是,我們在這裏只貼一下參數更新的推導過程公式,
線性迴歸模型的代價函數是下面 下麪這樣子:
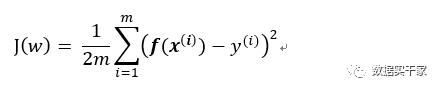
其中,f(x)爲:
![]()
我們的目標是求最小J(w)
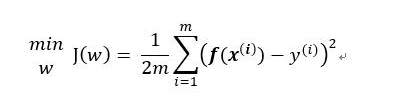
即在當J(w)取最小值時,對應的W的值,這時候梯度下降就用上了,用公式可表示爲如下樣式:
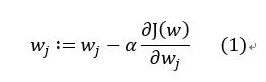
我們把J(w)對w的偏導求出來:
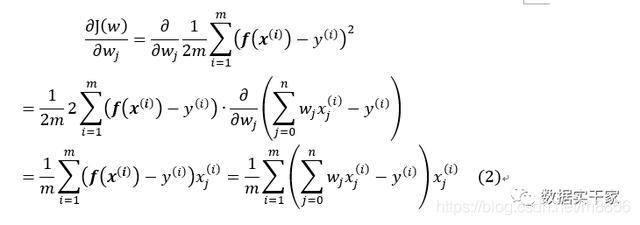
把(2)帶入(1)可得:

以上就是線性迴歸中的梯度下降演算法。
下面 下麪我們貼上程式碼,程式碼中會有比較詳細的註釋,在這裏就不多廢話了。
MultipleLinearRegressionTest.h:
//
// Created by lenovo on 2020/7/26.
//
#ifndef MULTIPLELINEARREGRESSION_MULTIPLELINEARREGRESSIONTEST_H
#define MULTIPLELINEARREGRESSION_MULTIPLELINEARREGRESSIONTEST_H
//初始化參數
void init_test(double learning_rate, long int X_Len,long int X_arg_count,int channel,double *y_pred_pt,double* theta_pt,double* temp_pt);
//開始訓練
void fit_test(double *X_pt,double *Y_pt);
#endif //MULTIPLELINEARREGRESSION_MULTIPLELINEARREGRESSIONTEST_H
MultipleLinearRegressionTest.c:
//
// Created by lenovo on 2020/7/26.
//
#include <stdio.h>
#include "MultipleLinearRegressionTest.h"
// 樣本個數,這裏其實是bachsize的意思,只不過我們只有一個bach
long int g_data_len = 10;
//學習率
double g_learning_rate = 0.01;
//參數個數
long int g_param_count = 6;
//通道數
int g_channel = 1;
double g_out_Y_pt = 0;
//預測輸出值指針
double *g_pred_pt = 0;
//參數指針
double *g_theta_pt = 0;
double *temp = 0;
//損失值
double loss_val = 1.0;
//初始化各個參數
void init_test(double learning_rate, long int data_len,long int param_count,int channel,double *y_pred_pt,double* theta_pt,double*temp_pt){
g_learning_rate = learning_rate;
g_data_len = data_len;
g_param_count = param_count;
g_channel = channel;
g_pred_pt = y_pred_pt;
g_theta_pt = theta_pt;
temp = temp_pt;
}
//更新參數值
void train_step_test(const double *temp_step, double *theta) {
for (int i = 0; i < g_param_count; i++) {
//這裏的temp_step[i] 其實就是算出來的梯度值
theta[i] = theta[i] - temp_step[i];
printf(" theta[%d] = %f\n",i, theta[i]);
}
}
//計算一個樣本的輸出值 y = WX + b
double f_test(const double *train_x_item,const double *theta){
g_out_Y_pt = -1;
for (int i = 0; i < g_param_count; ++i) {
g_out_Y_pt += theta[i]*(*(train_x_item+i));
}
return g_out_Y_pt;
}
//預測
double* predict_test(double *train_x,double *theta){
for (int i = 0; i < g_data_len; ++i) {
g_pred_pt[i] = f_test(train_x+i*g_param_count,theta);
}
return g_pred_pt;
}
//求損失
double loss_test(double *train_x,const double *train_y,
double *theta,double loss_val){
predict_test(train_x,theta);
loss_val = -1;
for (int i = 0; i < g_data_len; i++) {
loss_val += (train_y[i] - g_pred_pt[i]) * (train_y[i] - g_pred_pt[i]);
}
//次數計算的是一個bachsize 的平均損失(避免個別離羣值引起過擬合)
loss_val = loss_val / g_data_len;
printf(" loss_val = %f\n", loss_val);
return loss_val;
}
//求梯度
void calc_gradient_test(const double *train_x, const double *train_y,
double *temp_step, double *theta) {
//對每個參數分別子梯度
for (int i = 0; i < g_param_count; i++) {
double sum = 0;
//用一個bachsize的平均梯度表示當前參數的梯度(temp_step[i])
for (int j = 0; j < g_data_len; j++) {
double hx = 0;
for (int k = 0; k < g_param_count; k++) {
hx += theta[k] * (*(train_x+j*g_param_count+k));
}
sum += (hx - train_y[j]) * (*(train_x+j*g_param_count+i));
}
temp_step[i] = sum / g_data_len * 0.01;
}
printf("--------------------\n");
train_step_test(temp_step, theta);
}
// 開始訓練 (次數迭代60000次)
void fit_test(double *X_pt,double *Y_pt) {
for (int i = 0; i < 60000; ++i) {
printf("\nstep %d: \n", i);
calc_gradient_test(X_pt,Y_pt,temp,g_theta_pt);
loss_val = loss_test(X_pt,Y_pt,g_theta_pt,loss_val);
}
}
main.c :
#include "src/MultipleLinearRegressionTest.h"
int main() {
//該數據由 Y= 4*X1 + 9*X2 + 10*X3 + 2*X4 + 1*X5 + 6 產生(數據中尚爲加入噪聲)
//數據總的第一列都設定爲1,是爲了表示截距(Y=WX+B)的參數
double X_pt[10][6] = {{1, 7.41, 3.98, 8.34, 8.0, 0.95},
{1, 6.26, 5.12, 9.57, 0.3, 7.79},
{1, 1.52, 1.95, 4.01, 7.96, 2.19},
{1, 1.91, 8.58, 6.64, 2.99, 2.18},
{1, 2.2, 6.88, 0.88, 0.5, 9.74},
{1, 5.17, 0.14, 4.09, 9.0, 2.63},
{1, 9.13, 5.54, 6.36, 9.98, 5.27},
{1, 1.17, 4.67, 9.02, 5.14, 3.46},
{1, 3.97, 6.72, 6.12, 9.42, 1.43},
{1, 0.27, 3.16, 7.07, 0.28, 1.77}};
double Y_pt[10] = {171.81, 181.21, 87.84, 165.42, 96.26, 89.47, 181.21, 156.65, 163.83, 108.55};
double pred_pt[10] ={1,2,3,4,5,6,7,8,9,0};
// 參數
double theta_pt[6] = {1.0,1.0,1.0,1.0,1.0,2.0};
//臨時變數
double temp_pt[6] = {1.0,1.0,1.0,1.0,1.0,2.0};
// 學習率(次數我們還是指定爲一個固定值)
double learning_rate = 0.02;
// 樣本個數
int data_len = 10;
// 參數個數
int param_count = 6;
//通道數
int channel = 1;
init_test(learning_rate, data_len,param_count,channel,pred_pt,theta_pt,temp_pt);
fit_test((double *) X_pt, Y_pt);
return 0;
}
以上便是線性歸回模型梯度下降求解的程式碼實現。各位大俠如有疑問或者問題歡迎交流。