【論文翻譯】Clustering by Passing Messages Between Data Points

Clustering by Passing Messages Between Data Points

Brendan J. Frey*, Delbert Dueck

通過在數據點之間傳遞訊息進行聚類

Abstract: Clustering data by identifying a subset of representative examples is important for processing sensory signals and detecting patterns in data. Such 「exemplars」 can be found by randomly choosing an initial subset of data points and then iteratively refining it, but this works well only if that initial choice is close to a good solution. We devised a method called 「affinity propagation,」 which takes as input measures of similarity between pairs of data points. Real-valued messages are exchanged between data points until a high-quality set of exemplars and corresponding clusters gradually emerges. We used affinity propagation to cluster images of faces, detect genes in microarray data, identify representative sentences in this manuscript, and identify cities that are efficiently accessed by airline travel. Affinity propagation found clusters with much lower error than other methods, and it did so in less than one-hundredth the amount of time.

摘要

通過識別一個有代表性的例子子集來聚類數據對於處理感覺信號和檢測數據中的模式是很重要的。這樣的「範例」可以通過隨機選擇數據點的初始子集，然後迭代地細化它來找到，但是隻有當初始選擇接近一個好的解決方案時，這種方法才能 纔能很好地工作。我們設計了一種稱爲「親和傳播」的方法，它將數據點對之間的相似性作爲輸入度量。實值訊息在數據點之間交換，直到一組高品質的範例和相應的叢集逐漸出現。我們使用親和傳播對人臉影象進行聚類，檢測微陣列數據中的基因，識別手稿中的代表性句子，以及識別航空旅行可有效存取的城市。親和力傳播發現聚類誤差比其他方法要小得多，而且只花了不到百分之一的時間。

正文
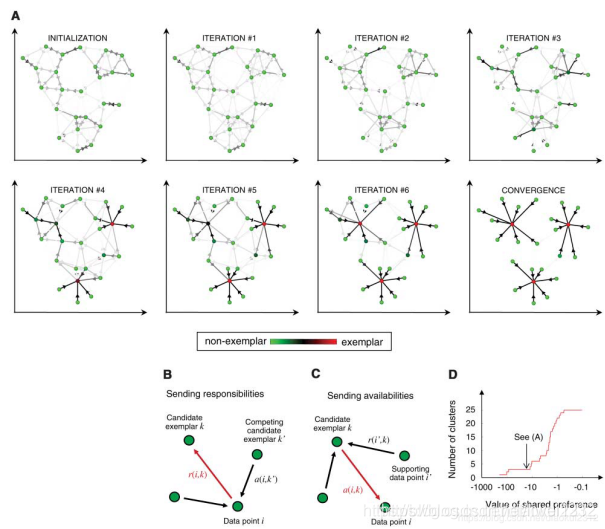
Clustering data based on a measure of similarity is a critical step in scientific data analysis and in engineering systems. A common approach is to use data to learn a set of centers such that the sum of squared errors between data points and their nearest centers is small. When the centers are selected from actual data points, they are called 「exemplars.」 The popular k-centers clustering　technique (1) begins with an initial set of randomly selected exemplars and iteratively refines this set so as to decrease the sum of squared errors. k-centers clustering is quite sensitive to the initial selection of exemplars, so it is usually rerun many times with different initializations in an attempt to find a good solution. However,this works well only when the number of clusters is small and chances are good that at least one random initialization is close to a good solution. We take a quite different approach and introduce a method that simultaneously considers all data points as potential exemplars. By viewing each data point as a node in a network, we devised a method that recursively transmits real-valued messages along edges of the network until a good set of exemplars and corresponding clusters emerges.As described later, messages are updated on the basis of simple formulas that search for　minima of an appropriately chosen energy function. At any point in time, the magnitude of each message reflects the current affinity that one data point has for choosing another data point as its exemplar, so we call our method 「affinity propagation.」 Figure 1A illustrates how clusters gradually emerge during the message-passing procedure.
基於相似性度量的聚類是科學數據分析和工程系統中的關鍵步驟。一種常見的方法是使用數據來學習一組中心，這樣數據點與其最近的中心之間的平方誤差之和很小。當這些中心是從實際數據點中選擇的時，稱之爲「樣本」。流行的k中心聚類技術（1）首先從隨機選擇的樣本集開始，然後迭代地細化該集合，以減少誤差平方和。k-中心聚類對樣本的初始選擇非常敏感，因此通常會用不同的初始化方法多次重新執行，試圖找到一個好的解決方案。但是，只有當叢集的數量很小，並且至少有一個隨機初始化很有可能接近一個好的解決方案時，這種方法才能 纔能很好地工作。我們採用了一種完全不同的方法，並引入了一種同時將所有數據點視爲潛在樣本的方法。通過將每個數據點視爲網路中的一個節點，我們設計了一種方法，該方法沿着網路的邊緣遞回地傳遞實值資訊，直到出現一組良好的樣本和相應的簇。如後文所述，在簡單公式的基礎上更新訊息，這些公式搜尋適當選擇的能量函數的最小值。在任何時間點，每個訊息的大小都反映了一個數據點選擇另一個數據點作爲樣本的當前親和力，因此我們將我們的方法稱爲「親和力傳播」。圖1A說明了在訊息傳遞過程中叢集是如何逐漸出現的。

Affinity propagation takes as input a collection of real-valued similarities between data points, where the similarity s(i,k) indicates how well the data point with index k is suited　to be the exemplar for data point i. When the goal is to minimize squared error, each similarity is set to a negative squared error (Euclidean distance): For points xi and xk, s(i,k) =−||xi − xk||2 . Indeed, the method described here can be applied when the optimization criterion is much more general. Later, we describe tasks where similarities are derived for pairs of images, pairs of microarray measurements, pairs of English sentences, and pairs of cities. When an exemplar-dependent probability model is available, s(i,k) can be set to the log-likelihood of data point i given that its exemplar is point k. Alternatively, when appropriate, similarities may be set by hand.

親和力的傳播將數據點間的實值相似性的集合作爲輸入，其中，相似度s(i,k)表示索引爲k的數據點很適合作爲數據點i的樣本。當目標是最小化平方誤差時，將每個相似度被設定爲一個負的平方誤差(歐氏距離):對於點 xi 和 xk, s(i,k) =−||xi − xk||2，實際上，這裏描述的方法可以在優化準則更一般的情況下應用。隨後，我們描述的任務中，相似性是由成對的影象、成對的微陣列測量、成對的英語句子和成對的城市得出的。當一個樣本相關的概率模型可用時，s(i,k)可以被設爲數據點i的對數似然，假設它的樣本是點k。或者，在適當的時候，可以手工設定相似性。

Rather than requiring that the number of clusters be prespecified, affinity propagation takes as input a real number s(k,k) for each data point k so that data points with larger values of s(k,k) are more likely to be chosen as exemplars. These values are referred to as 「preferences.」 The number of identified exemplars (number of clusters) is influenced by the values of the input preferences, but also emerges from the message-passing procedure. If a priori, all data points are equally suitable as exemplars, the preferences should be set to a common value—this value can be varied to produce different numbers of clusters. The shared value could be the median of the input similarities (resulting in a moderate number of clusters) or their minimum (resulting in a small number of clusters).

親和力傳播是對每個數據點k取一個實數s(k,k)作爲輸入，這樣s(k,k)值越大的數據點更有可能被選擇爲樣本，而不是預先指定聚類的數量。這些值稱爲「偏好設定」。識別出的樣本的數量(聚類的數量)受到輸入偏好值的影響，但也會從訊息傳遞過程中產生。如果先驗條件下，所有數據點都同樣適合作爲樣本，那麼偏好應該設定爲一個同樣的值——這個值可以被改變以產生不同數量的聚類。共用值可以是輸入相似性的中值(導致聚類數量適中)，也可以是它們的最小值(導致聚類數量較少)。

There are two kinds of message exchanged between data points, and each takes into account a different kind of competition. Messages can be combined at any stage to decide which points are exemplars and, for every other point, which exemplar it belongs to. The「responsibility」 r(i,k), sent from data point i to candidate exemplar point k, reflects the accumulated evidence for how well-suited point k is to serve as the exemplar for point i, taking into account other potential exemplars for point i (Fig. 1B). The 「availability」 a(i,k), sent from candidate exemplar point k to point i,reflects the accumulated evidence for how appropriate it would be for point i to choose point k as its exemplar, taking into account the support from other points that point k should be an exemplar (Fig. 1C). r(i,k) and a(i,k) can be viewed as log-probability ratios. To begin with, the availabilities are initialized to zero:a(i,k) = 0. Then, the responsibilities are computed using the rule

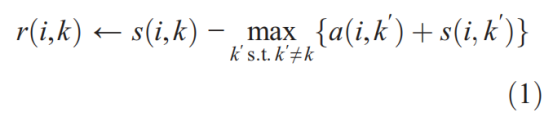
In the first iteration, because the availabilities are zero, r(i,k) is set to the input similarity between point i and point k as its exemplar,minus the largest of the similarities between point i and other candidate exemplars. This competitive update is data-driven and does not take into account how many other points favor each candidate exemplar. In later iterations, when some points are effectively assigned to other exemplars, their availabilities will drop below zero as prescribed by the update rule below. These negative availabilities will decrease the effective values of some of the input similarities s(i,k′) in the above rule, removing the corresponding candidate exemplars from competition. For k = i, the responsibility r(k,k) is set to the input preference that point k be chosen as an exemplar, s(k,k), minus the largest of the similarities between point i and all other candidate exemplars. This 「self-responsibility」 reflects accumulated evidence that point k is an exemplar, based on its input preference tempered by how ill-suited it is to be assigned to another exemplar.
數據點之間交換的訊息有兩種，每一種都考慮到競爭的不同類型。訊息可以在任何階段進行組合，以決定哪些點是樣本，對於每個其他的點，它屬於哪些樣本。「責任」r(i,k)，從數據點i發送到候選樣本點k，反映了積累的證據，表明k點是多麼適合作爲第i點的樣本，考慮到第i點的其他潛在樣本(圖1B)。「可用性」a(i,k)，從候選樣本點k發送到點i，反映了積累的證據，說明點i選擇點k作爲它的樣本是多麼合適，考慮到其他點的支援，認爲點k應該是一個樣本(圖1C)。r(i,k) 和 a(i,k)可以看成是對數概率比。首先，可用性被初始化爲零:a(i,k) = 0。然後，使用規則計算職責
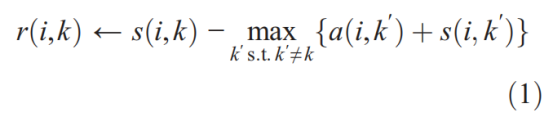在第一次迭代中，由於可用性爲0,r(i,k)設爲作爲樣本的點i和點k之間的輸入相似度，減去點i和其他候選樣本之間的相似度的最大值。這個競爭性的更新是數據驅動的，並且沒有考慮有多少其他點有利於每個候選樣本。在以後的迭代中，當一些點被有效地分配給其他樣本時，它們的可用性將會降到0以下，這是下面 下麪的更新規則所規定的。這些負可用性會降低上述規則中某些輸入相似點s(i,k’)的有效值，使相應的候選樣本從競爭中消失。對於k = i，責任r(k,k)被設爲點k被選爲樣本的輸入偏好s(k,k)，減去點i和所有候選樣本之間最大的相似性。這種「自我責任」反映了k點是一個樣本的積累證據，基於它的輸入偏好再加上它有多不適合被分配到另一個範例。

Whereas the above responsibility update lets all candidate exemplars compete for ownership of a data point, the following availability update gathers evidence from data points as to whether each candidate exemplar would make a good exemplar:

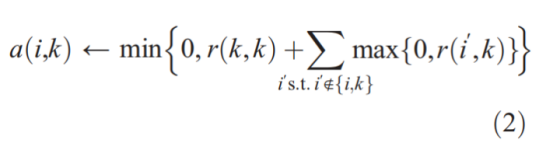
The availability a(i,k) is set to the self-responsibility r(k,k) plus the sum of the positive responsibilities candidate exemplar k receives from other points. Only the positive portions of incoming responsibilities are added, because it is only necessary for a good exemplar to explain some data points well (positive responsibilities),regardless of how poorly it explains other data points (negative responsibilities). If the self-responsibility r(k,k) is negative (indicating that point k is currently better suited as belonging to another exemplar rather than being an exemplar itself), the availability of point k as an exemplar can be increased if some other points have positive responsibilities for point k being their exemplar. To limit the influence of strong incoming positive responsibilities, the total sum is thresholded so that it cannot go above zero. The 「self-availability」 a(k,k) is updated differently:

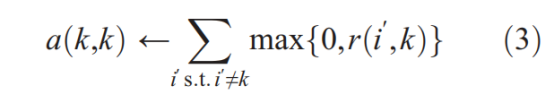
This message reflects accumulated evidence that point k is an exemplar, based on the positive responsibilities sent to candidate exemplar k from other points.

上面的職責更新讓所有候選範例爲數據點的所有權而競爭，以下可用性更新從數據點收集證據，以確定每個候選範例是否會成爲一個好範例:
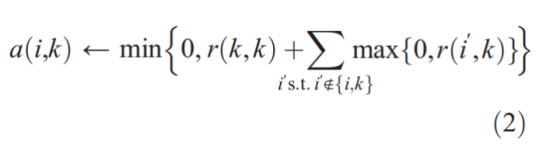可用性a(i,k)被設爲自我責任r(k,k)加上候選範例k從其他點接收到的正責任的總和。
只增加傳入責任的積極部分，因爲一個好的範例只需要很好地解釋一些數據點(積極的責任)，而不管它對其他數據點的解釋有多差(消極的責任)。如果自我責任r (k, k)是負的(表明點k是目前適合屬於另一個樣本,而不是作爲一個樣本本身),如果其他點對作爲範例的點有積極的責任，那麼k點作爲範例的可用性就會增加。爲了限制傳入的積極責任的影響，總和是有閾值的，因此不能超過零。「自我可用性」a(k,k)的更新方式不同:

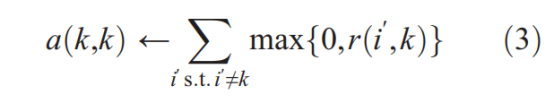
這條訊息反映了基於從其他點發送給候選範例k的積極責任所積累的證據，證明點k是一個範例。

The above update rules require only simple,local computations that are easily implemented (2), and messages need only be exchanged between pairs of points with known similarities. At any point during affinity propagation, availabilities and responsibilities can be combined to identify exemplars. For point i, the value of k that maximizes a(i,k) + r(i,k) either identifies point i as an exemplar if k = i, or identifies the data point that is the exemplar for point i. The message-passing procedure may be terminated after a fixed number of iterations, after changes in the messages fall below a threshold, or after the local decisions stay constant for some number of iterations. When updating the messages,it is important that they be damped to avoid numerical oscillations that arise in some circumstances. Each message is set to l times its value from the previous iteration plus 1 – λ times its prescribed updated value, where the damping factor l is between 0 and 1. In all of our experiments (3), we used a default damping factor of λ = 0.5, and each iteration of affinity propagation consisted of (i) updating all responsibilities given the availabilities, (ii) updating all availabilities given the responsibilities, and (iii) combining availabilities and responsibilities to monitor the exemplar decisions and terminate the algorithm when these decisions did not change for 10 iterations.
上面的更新規則只需要簡單的、容易實現的本地計算(2)，並且只需要在已知相似點對之間交換訊息。在親和傳播期間的任何點，可用性和職責都可以組合起來識別樣本。對於點i，使a(i,k) + r(i,k)最大化的k的值，如果k = i，可以將點i識別爲一個樣本，或者識別爲點i的樣本數據點。訊息傳遞過程可以在固定次數的迭代之後終止，也可以在訊息中的更改低於閾值之後終止，或者在本地決策一定次數的迭代中保持不變之後終止。在更新資訊時，重要的是要對它們進行阻尼，以避免在某些情況下出現的數值振盪。每條訊息被設定爲λ乘以它在以前的迭代中得到的值加上1 -λ 乘以它所規定的更新值，其中阻尼因子λ在0到1之間。(3)我們所有的實驗中,我們使用一個預設的阻尼因子λ= 0.5,和每次迭代的親和力傳播包括(i)更新所有責任考慮到可用性,(2)更新所有可用性的責任,和(3)結合可用性和責任監督樣本決定,終止演算法當10次迭代中這些決定不改變。

Figure 1A shows the dynamics of affinity propagation applied to 25 two-dimensional data points (3), using negative squared error as the similarity. One advantage of affinity propagation is that the number of exemplars need not be specified beforehand. Instead, the appropriate number of exemplars emerges from the message passing method and depends on the input exemplar preferences. This enables automatic model selection, based on a prior specification of how preferable each point is as an exemplar. Figure 1D shows the effect of the value of the common input preference on the number of clusters. This relation is nearly identical to the relation found by exactly minimizing the squared error (2).
圖1A顯示了應用於25個二維數據點(3)的親和傳播動力學，使用負平方誤差作爲相似性。關聯傳播的一個優點是不需要預先指定範例的數量。相反，從資訊傳遞方法中會出現適當數目的範例，並取決於輸入範例的偏好。這使得自動的模型選擇成爲可能，基於對每個點作爲範例的可取程度的預先說明。圖1D顯示了公共輸入偏好的值對叢集數量的影響。這個關係與精確地最小化平方誤差(2)所發現的關係幾乎相同。

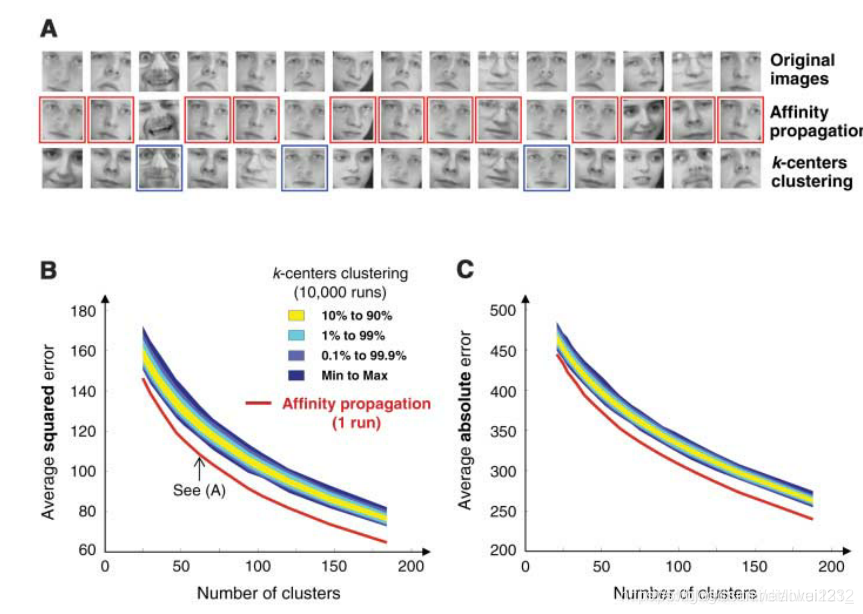
We next studied the problem of clustering images of faces using the standard optimization criterion of squared error. We used both affinity propagation and k-centers clustering to identify exemplars among 900 grayscale images extracted from the Olivetti face database (3). Affinity propagation found exemplars with much lower squared error than the best of 100 runs of k-centers clustering (Fig. 2A), which took about the same amount of computer time.We asked whether a huge number of random restarts of k-centers clustering could achieve the same squared error. Figure 2B shows the error achieved by one run of affinity propagation and the distribution of errors achieved by 10,000 runs of k-centers clustering, plotted against the number of clusters. Affinity propagation uniformly achieved much lower error in more than two orders of magnitude less time. Another popular optimization criterion is the sum of absolute pixel differences (which better tolerates outlying pixel intensities), so we repeated the above procedure using this error measure. Affinity propagation again uniformly achieved lower error (Fig. 2C).
接下來，我們利用平方誤差的標準優化準則研究了人臉影象聚類問題。我們使用親和傳播和k-中心聚類來識別從Olivetti人臉數據庫（3）中提取的900幅灰度影象樣本。親和力傳播發現樣本的平方誤差遠低於k-中心聚類（圖2A）100次中最好的一次，後者花費了大約相同的計算機時間。我們詢問大量隨機重新啓動k-中心聚類是否可以獲得相同的平方誤差。圖2B顯示了一次親和力傳播所獲得的誤差，以及10000次k-中心聚類所獲得的誤差分佈，並根據聚類的數量繪製。親和傳播在兩個數量級以上的時間內均勻地獲得了更低的誤差。另一個流行的優化標準是絕對畫素差的總和（它可以更好地容忍離羣的畫素強度），因此我們使用這個誤差度量重複上述過程。親和傳播再次均勻地獲得較低的誤差（圖2C）。

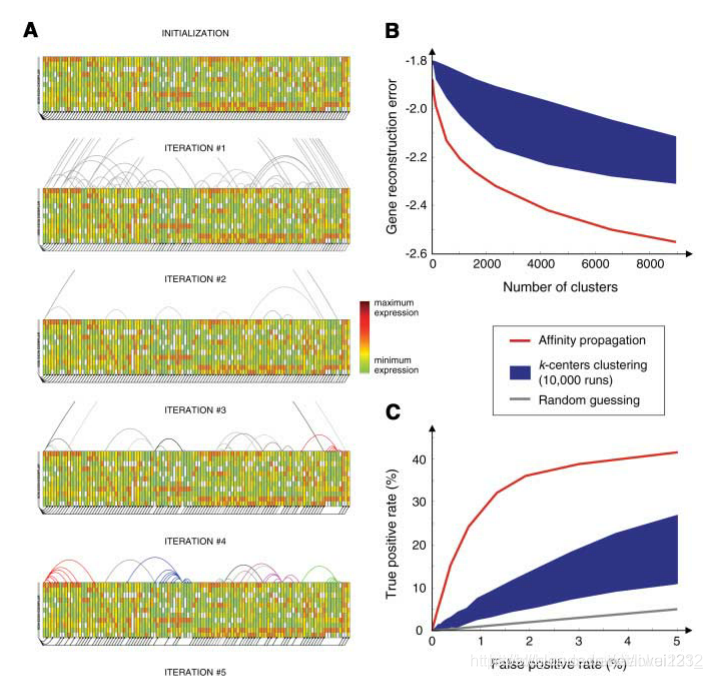
Many tasks require the identification of exemplars among sparsely related data, i.e., where most similarities are either unknown or large and negative. To examine affinity propagation in this context, we addressed the task of clustering putative exons to find genes, using the sparse similarity matrix derived from microarray data and reported in (4). In that work, 75,066 segments of DNA (60 bases long) corresponding to putative exons were mined from the genome of mouse chromosome 1. Their transcription levels were measured across 12 tissue samples, and the similarity between every pair of putative exons (data points) was computed. The measure of similarity between putative exons was based on their proximity in the genome and the degree of coordination of their transcription levels across the 12 tissues. To account for putative exons that are not exons (e.g., introns), we included an additional artificial exemplar and determined the similarity of each other data point to this 「non-exon exemplar」 using statistics taken over the entire data set. The resulting 75,067 × 75,067 similarity matrix (3) consisted of 99.73% similarities with values of −∞, corresponding to distant DNA segments that could not possibly be part of the same gene. We applied affinity propagation to this similarity matrix, but because messages need not be exchanged between point i and k if s(i,k) = −∞, each iteration of affinity propagation required exchanging messages between only a tiny subset (0.27% or 15million) of data point pairs.
許多工需要在稀疏相關的數據中識別樣本，也就是說，在這些數據中，大多數相似性要麼是未知的，要麼是大而負面的。爲了研究這種背景下的親和力傳播，我們利用從微陣列數據和報告（4）中導出的稀疏相似性矩陣，聚類假定的外顯子找到基因。在這項研究中，我們從小鼠1號染色體的基因組中提取了75066段DNA片段（60鹼基長），這些片段與假定的外顯子相對應。在12個組織樣本中測量了它們的轉錄水平，並計算了每對假定外顯子（數據點）之間的相似性。假設外顯子之間的相似性是基於它們在基因組中的接近程度以及它們在12種組織中轉錄水平的協調程度。爲了解釋不是外顯子的假定外顯子（例如內含子），我們加入了一個額外的人工樣本，並使用對整個數據集的統計數據來確定其他數據點與這個「非外顯樣本」的相似性。由此得到的75067×75067相似矩陣（3）與-∞值的相似度爲99.73%，對應於不可能是同一基因一部分的遠緣DNA片段。我們將相似性傳播應用到這個相似性矩陣中，但是由於如果s（i，k）=-∞時，不需要在點i和k之間交換訊息，所以親合傳播的每次迭代只需要在數據點對的一小部分（0.27%或1500萬）之間交換訊息。

Figure 3A illustrates the identification of gene clusters and the assignment of some data points to the nonexon exemplar. The reconstruction errors for affinity propagation and k-centers clustering are compared in Fig. 3B.For each number of clusters, affinity propagation was run once and took 6 min, whereas k-centers clustering was run 10,000 times and took 208 hours. To address the question of how well these methods perform in detecting bona fide gene segments, Fig. 3C plots the truepositive (TP) rate against the false-positive (FP) rate, using the labels provided in the RefSeq database (5). Affinity propagation achieved significantly higher TP rates, especially at low FP rates, which are most important to biologists. At a FP rate of 3%, affinity propagation achieved a TP rate of 39%, whereas the best k-centers clustering result was 17%. For comparison, at the same FP rate, the best TP rate for hierarchical agglomerative clustering (2) was 19%, and the engineering tool described in (4), which accounts for additional biological knowledge, achieved a TP rate of 43%.
圖3A說明了基因聚類的識別和將一些數據點的分配給非外顯樣本。圖3B中比較了親和傳播和k-中心聚類的重建誤差。對於每個聚類數，親和力傳播執行一次，花費6分鐘；而k-中心聚類則執行10000次，花費208小時。爲了解決這些方法在檢測真實基因片段方面的表現如何的問題，圖3C使用RefSeq數據庫（5）中提供的標籤繪製了真陽性（TP）率和假陽性（FP）率。親和力繁殖獲得了顯著較高的TP率，尤其是在低FP率下，這對生物學家來說是最重要的。當FP率爲3%時，親和繁殖的TP率爲39%，而k-中心聚類的最好結果爲17%。作爲比較，在相同的FP率下，層次聚集聚類（2）的最佳TP率爲19%，而（4）中描述的工程工具（它解釋了額外的生物學知識）實現了43%的TP率。

Affinity propagation’s ability to operate on the basis of nonstandard optimization criteria makes it suitable for exploratory data analysis using unusual measures of similarity. Unlike metricspace clustering techniques such as k-means clustering (1), affinity propagation can be applied to problems where the data do not lie in a continuous space. Indeed, it can be applied to problems where the similarities are not symmetric [i.e., s(i,k) ≠ s(k,i)] and to problems where the similarities do not satisfy the triangle inequality [i.e., s(i,k) < s(i,j) + s( j,k)]. To identify a small number of sentences in a draft of this manuscript that summarize other sentences, we treated each sentence as a 「bag of words」 (6) and computed the similarity of sentence i to sentence k based on the cost of encoding the words in sentence i using the words in sentence k. We found that 97% of the resulting similarities (2, 3) were not symmetric. The preferences were adjusted to identify (using l = 0.8) different numbers of representative exemplar sentences (2), and the solution with four sentences is shown in Fig. 4A.

親和力傳播基於非標準優化準則的操作能力使得它適合於使用不尋常的相似性度量進行探索性數據分析。不像度量空間聚類的技術，例如k-均值聚類（1），親和傳播可以應用於數據不在連續空間中的問題。實際上，它可以被應用於相似性不對稱的問題[即s（i，k）≠s（k，i）]和相似性不滿足三角形不等式[即s(i,k) < s(i,j) + s( j,k)]的問題。爲了找出本文草稿中總結其他句子的少量句子，我們將每個句子視爲一個「單詞包」（6），並根據k句子中單詞的編碼成本計算出句子與k句子的相似度。我們發現97%的相似性（2，3）不是對稱的。調整偏好以識別（使用l=0.8）不同數量的代表性例句（2），四個句子的解決方案如圖4A所示。

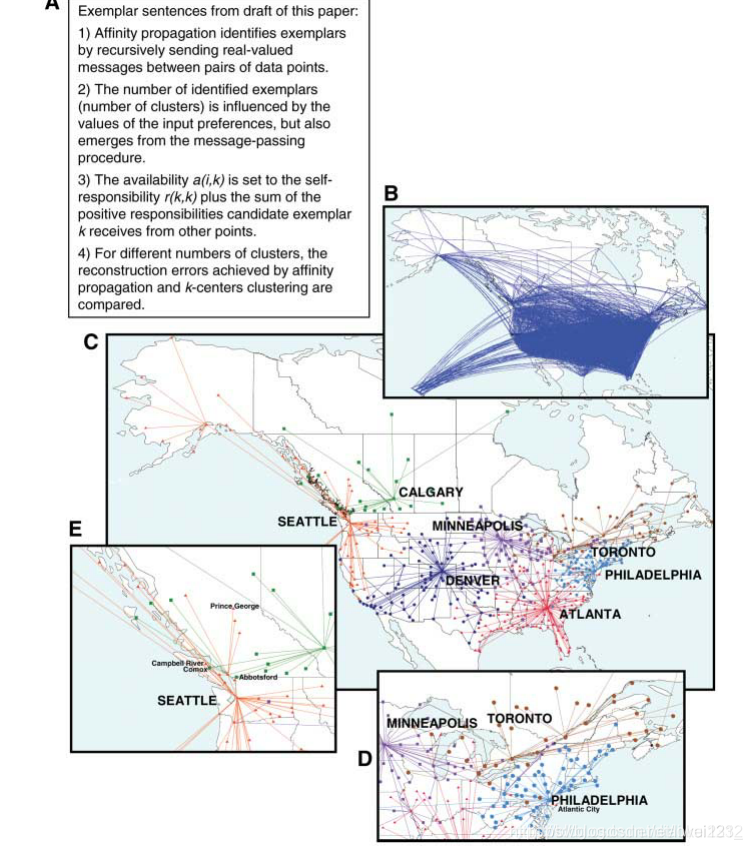
We also applied affinity propagation to explore the problem of identifying a restricted number of Canadian and American cities that are most easily accessible by large subsets of other cities, in terms of estimated commercial airline travel time. Each data point was a city, and the similarity s(i,k) was set to the negative time it takes to travel from city i to city k by airline, including estimated stopover delays (3). Due to headwinds, the transit time was in many cases different depending on the direction of travel, so that 36% of the similarities were asymmetric. Further, for 97% of city pairs i and k, there was a third city j such that the triangle inequality was violated, because the trip from i to k included a long stopover delay n city j so it took longer than the sum of the durations of the trips from i to j and j to k. When the number of 「most accessible cities」 was constrained to be seven (by adjusting the input preference appropriately), the cities shown in Fig. 4, B to E, were identified. It is interesting that several major cities were not selected, either because heavy international travel makes them inappropriate as easily accessible domestic destinations (e.g., New YorkCity, Los Angeles) or because their neighborhoods can be more efficiently accessed through other destinations (e.g., Atlanta, Philadelphia, and Minneapolis account for Chicago’s destinations, while avoiding potential airport delays).
我們還應用親和力傳播來探索確定有限數量的加拿大和美國城市的問題，這些城市最容易被其他大城市的子集所存取，根據估計的商業航空旅行時間。每個數據點都是一個城市，相似性s（i，k）被設定爲乘飛機從城市i到城市k所需的負時間，包括估計的中途停留延誤（3）。由於逆風，在許多情況下，運輸時間依賴於旅行方向，因此36%的相似性是不對稱的。此外，對於97%的城市對i和k，有第三個城市j違反了三角不等式，因爲從i到k的行程包括在城市j的長的中途停留延遲，所以它比從i到j和j到k的旅行時間總和要長。當「最容易到達的城市」的數量被限製爲7（通過適當地調整輸入偏好），圖4中B到E所示的城市被識別。有趣的是，幾個主要城市沒有被選中，要麼是因爲大量的國際旅行使得它們不適合作爲容易到達的國內目的地（如紐約市、洛杉磯），要麼是因爲它們的社羣可以通過其他目的地更有效地到達（如亞特蘭大、費城，明尼阿波利斯是芝加哥的目的地，同時避免了潛在的機場延誤）。

Affinity propagation can be viewed as a method that searches for minima of an energy function (7) that depends on a set of N hidden labels, c1,…,cN, corresponding to the N data points. Each label indicates the exemplar to which the point belongs, so that s(i,ci) is the similarity of data point i to its exemplar. ci = i is a special case indicating that point i is itself an exemplar, so that s(i,ci) is the input preference for point i. Not all configurations of the labels are valid; a configuration c is valid when for every point i, if some other point i′ has chosen i as its exemplar (i.e., ci′ = i), then i must be an exemplar (i.e., ci = i). The energy of a valid configuration is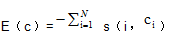
Exactly minimizing the energy is computationally intractable, because a special case of this minimization problem is the NP-hard k-median problem (8). However, the update rules for affinity propagation correspond to fixed-point recursions for minimizing a Bethe free-energy (9) approximation. Affinity propagation is most easily derived as an instance of the max-sum algorithm in a factor graph (10) describing the constraintson the labels and the energy function (2).
親和傳播可以看作是一種搜尋能量函數（7）的極小值的方法，該能量函數依賴於與N個數據點相對應的一組N個隱藏標籤c1，…，cN。每個標籤都表示該點所屬的樣本，因此s（i，ci）是數據點i與其範例的相似性。ci=i是一個特例，表明i點本身就是一個樣本，因此s（i，ci）是點i的輸入偏好。並非所有標籤的設定都有效；設定c是有效的，當對於每個點i，如果其他點i’選擇i作爲其樣本（即ci=i），那麼i必須是一個範例（即ci=i）。有效設定的能量爲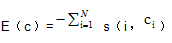

精確地最小化能量在計算上是困難的，因爲這個最小化問題的一個特例是NP難k-中值問題（8）。然而，親合傳播的更新規則對應於最小化Bethe自由能（9）近似的不動點遞回。親和力傳播作爲因子圖（10）中描述標籤約束和能量函數（2）的最大和演算法的範例最容易導出。然而，親合傳播的更新規則對應於最小化Bethe自由能（9）近似的不動點遞回。親和力傳播作爲因子圖（10）中描述標籤約束和能量函數（2）的最大和演算法的範例最容易導出。

In some degenerate cases, the energy function may have multiple minima with corresponding multiple fixed points of the update rules, and these may prevent convergence. For example, if s(1,2) = s(2,1) and s(1,1) = s(2,2), then the solutions c1 = c2 = 1 and c1 = c2 = 2 both achieve the same energy. In this case, affinity propagation may oscillate, with both data points alternating between being exemplars and nonexemplars. In practice, we found that oscillations could always be avoided by adding a tiny amount of noise to the similarities to prevent degenerate situations,or by increasing the damping factor.
在某些退化情形下，能量函數可能具有多個極小值，且更新規則的多個不動點可能會阻止收斂。例如，如果s（1,2）=s（2,1）和s（1,1）=s（2,2），則解c1=c2=1和c1=c2=2都獲得相同的能量。在這種情況下，親和性傳播可能會振盪，兩個數據點在樣本和非樣本之間交替。在實踐中，我們發現通過在相似點上新增少量的噪聲來防止退化情況，或者通過增加阻尼因子來避免振盪。

Affinity propagation has several advantages over related techniques. Methods such as k-centers clustering (1), k-means clustering(1), and the expectation maximization (EM) algorithm (11) store a relatively small set of estimated cluster centers at each step. These techniques are improved upon by methods that begin with a large number of clusters and then prune them (12), but they still rely on random sampling and make hard pruning decisions that cannot be recovered from. In contrast, by simultaneously considering all data points as candidate centers and gradually identifying clusters, affinity propagation is able to avoid many of the poor solutions caused by unlucky initializations and hard decisions. Markov chain Monte Carlo techniques (13) randomly search for good solutions, but do not share affinity propagation’s advantage of considering many possible solutions all at once.
與相關技術相比，親和傳播有幾個優點。像k-中心聚類（1）、k-均值聚類（1）和期望最大化（EM）演算法（11）這樣的方法在每個步驟儲存一個相對較小的估計聚類中心集。
這些技術通過從大量的聚類開始，然後對它們進行修剪的方法得到了改進（12），但是它們仍然依賴於隨機抽樣，並且做出無法恢復的硬修剪決策。相反，通過同時考慮所有數據點作爲候選中心並逐步識別簇，親和傳播能夠避免由於不吉利的初始化和艱難的決策而導致的許多糟糕的解決方案。馬爾可夫鏈蒙特卡羅技術（13）隨機搜尋好的解決方案，但不共用親和傳播的優點，即一次考慮許多可能的解決方案。

Hierarchical agglomerative clustering (14) and spectral clustering (15) solve the quite different problem of recursively comparing pairs of points to find partitions of the data. These techniques do not require that all points within a cluster be similar to a single center and are thus not well-suited to many tasks. In particular, two points that should not be in the same cluster may be grouped together by an unfortunate sequence of pairwise groupings.
層次聚集聚類（14）和譜聚類（15）解決了遞回比較點對以找到數據分割區的完全不同的問題。這些技術並不要求一個聚類內的所有點都類似於一箇中心，因此不太適合許多工。特別是，不應該在同一個聚類中的兩個點可能會被一個不幸的成對分組序列組合在一起。

In (8), it was shown that the related metric k-median problem could be relaxed to form a
linear program with a constant factor approximation. There, the input was assumed to be metric, i.e., nonnegative, symmetric, and satisfying the triangle inequality. In contrast, affinity propagation can take as input general nonmetric similarities.Affinity propagation also provides a conceptually new approach that works well in practice. Whereas the linear programming relaxation is hard to solve and sophisticated software packages need to be applied (e.g., CPLEX), affinity propagation makes use of intuitive message updates that can be implemented in a few lines of code (2).
在（8）中，證明了相關的度量k-中值問題可以放寬到常係數近似線性規劃。在這裏，假設輸入是度量的，即非負的，對稱的，滿足三角不等式的。相反，親和傳播可以將一般非度量相似性作爲輸入。親和力傳播還提供了一種概念上新的方法，在實踐中效果良好。雖然線性規劃鬆弛很難解決，並且需要應用複雜的軟體包（例如，CPLEX），但親和傳播利用了可以在幾行程式碼中實現的直觀訊息更新（2）。

Affinity propagation is related in spirit to techniques recently used to obtain record-breaking results in quite different disciplines (16). The approach of recursively propagating messages (17) i n a 「loopy graph」 has been used to approach Shannon’s limit in error-correcting decoding (18, 19), solve random satisfiability problems with an order-of-magnitude increase in size (20), solve instances of the NP-hard twodimensional phase-unwrapping problem (21), and efficiently estimate depth from pairs of stereo images (22). Yet, to our knowledge, affinity propagation is the first method to make use of this idea to solve the age-old, fundamental problem of clustering data. Because of its simplicity, general applicability, and performance, we believe affinity propagation will prove to be of broad value in science and engineering.
親和力傳播在精神上與最近在不同學科中獲得破紀錄結果的技術有關（16）。在「回圈圖」中遞回傳播訊息（17）的方法被用於逼近糾錯解碼中的香農極限（18，19），解決大小增加一個數量級的隨機可滿足性問題（20），解決NP難二維相位展開問題（21），並有效地估計立體影象對的深度（22）。然而，據我們所知，親和力傳播是利用這種思想來解決古老的、基本的數據聚類問題的第一種方法。由於它的簡單性，普遍適用性和效能，我們相信親和傳播將被證明在科學和工程中具有廣泛的價值。